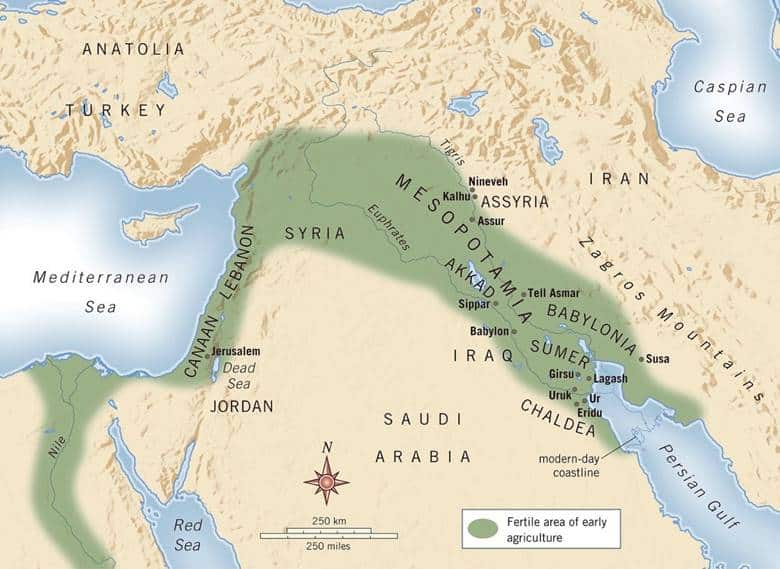
Sistemli matematiğin doğuşu hakkında kesin bir şey söylemek mümkün değildir. Ancak yine de bulgular bize yaklaşık M.Ö 3000 –2000 yılları civarında Mısır ve Mezopotamya bölgesini işaret eder. Gelişmiş bir sayı sistemi kullandığı bilinen ilk insanlar, günümüz Irak’ında Dicle ve Fırat nehirleri arasında bulunan adına Mezopotamya dediğimiz bölgede yaşayan Sümerlerdi. Kimilerine göre de matematik Mısır’da doğmuştur.
Her iki uygarlığın da matematiğinde teorem, formül ve ispat yoktur. Bulgular emprik veya deneysel; işlemler sayısaldır. Bunun böyle olması kaçınılmazdır zira o dönemde matematik, simgesel olarak değil, sözel olarak ifade edilmektedir.
Ancak şunu hatırlamak da fayda var. O zamanlarda matematik daha çok ihtiyaçları gidermeye odaklanmıştı. Bu ihtiyaçlar zaman-takvim belirlemek, muhasebe işleri ve inşaat, miras dağıtımı gibi şeylerdir. Bu ön bilgilerden sonra şimdi tarihe kısa bir yolculuk yapalım ve matematiğin doğuşuna şahit olalım.
Matematik, antik dünyada ilerleme için önemli bir itici güçtü. Onsuz bir toplum vergi toplayamaz, ürün kayıtlarını tutamaz veya piramitler gibi mimari harikalar tasarlayamazdı. Mısırlılar arazi ölçümleri, hasat verimi tahmini, vergilendirme gibi şeyleri doğru biçimde hesaplamak için geometri, cebir ve aritmetik kullandılar.
Mısır Matematiği Hakkında Neler Biliyoruz?
Günümüzde, Mısır matematiği ile ilgili bildiklerimiz temelinde iki papirüsten geliyor. Bu papirüslerden ilki, Ahmes (Rhind) papirüsü olarak bilinmektedir. Rhind papirüsü, MÖ 1.650 civarına tarihlenen bir belgedir. 1858 yılında İskoçyalı antikacı Alexander Henry Rhind tarafından Nil nehrinin Ramesseum yakınındaki Thebes’te bulunmuştur.

Kâtip Ahmes (M.Ö. 1680 – 1620) tarafından yazılan papirüs, 6 metre uzunluğunda ve 35 cm genişliğindedir. 1868 yılından beri British Museum’da sergilenmektedir. Eski Mısırlılar, muhasebe ve mühendislikteki görevleri yerine getirmek için aritmetiği kullanmakta çok ustaydılar. Bunu Rhind papirüsünde görebiliyoruz
Papirüs çarpma ve bölme işlemlerinin, denklem çözümlerinin, günlük pratik matematiksel hesaplamaların nasıl yapılacağına dair 85 problem içerir. Daha fazla detay için bu yazımıza göz atmalısınız: Firavunların Matematiği: Rhind Papirüsü ve Eski Mısır Matematiği
Moskova papirüsü diye bilinen ikinci papirüs de M.Ö. 1600 lerde yazılan bir kitapçıktır. Bu papirüs 25 soru içermektedir. Bu sorular, ikisi hariç, Ahmes papirüsündeki sorular türündendir. Ancak farklı olarak bu papirüs bizlere Mısırlıların alan, hacim hesaplamaları hakkında da ipuçları verir.
Papirüste, bir düzlemle kesilen küre parçasının hacmi ve yüzeyinin alanının hesaplanması yer alır. Ayrıca yine bir düzlemle kesilen bir piramidin hacminin bulunması da bulunur. Her iki soru da doğru olarak çözülmüştür. Bu iki soru Mısır matematiğinin zirvesi olarak kabul edilmektedir.
Mısır Matematiği Birim Kesirler Üzerine Kuruluydu
MÖ dördüncü bin yılın sonunda Mısırlıların kendi sayma sistemleri vardı. Bu sistem günümüzde kullandığımız onluk sisteme benziyordu. Ancak günümüzde kullandığımız rakamlar yerine 7 farklı sembol kullanıyorlardı. Her sembolün rakamsal bir karşılığı vardı. Bu sembolleri büyükten küçüğe sıralayarak da sayıları yazabiliyorlardı.

Mısırlılar yedi farklı sembol ile 9.999.999’a kadar herhangi bir sayıyı yazmayı başardılar. Ancak yazıkları şey bazen çok fazla sembol içermek zorundaydı. Örneğin 1.000.000 yazmak için 9 düz çizgi, 9 at nalı, 9 çengel diye devam ederek toplamda 54 karakter çizilmeliydi.
Aslında Mısır matematiğinin en önemli tarafı kesirlerle yapılan hesaplamalardır. Bütün kesirler payı bir olan ve birim kesir denilen kesirlerin toplamı şeklinde yazılabiliyordu. Bunlara Mısır kesirleri de denilmektedir. Birim kesirler yazım kolaylığı açısından paydadaki sayının üzerine bir çizgi çekilerek ifade ediliyordu. Bu ilginç sistemi başka bir yazıda ele almıştık. Detayları burada: Horus’un Gözü İle Matematiğin Ne İlgisi Var?
Mezopotamya Matematiği Hakkında Neler Biliyoruz?
Mezopotamya’da yaşamış medeniyetler, Mısırdan kalandan bin kat daha fazla yazılı belge kalmıştır. Bunun nedeni, Mezopotamyalıların yazı aracı olarak kil tabletleri kullanmalarıdır. Yapılan kazılarda yarım milyondan fazla tablet bulunmuştur. Bu tabletlerin önemli bir kısmı İstanbul arkeoloji müzesindedir. Diğerleri de dünyanın çeşitli – Berlin, Moskova, British, Louvre, Yel, Colombia ve Pensilvanya- müzelerindedir.

Bu bölgede yaşamış medeniyetlerin matematiği hakkında bilgimiz bu tabletlerden gelmektedir. Bu tabletlerden anlaşılan, Mezopotamya’da matematik, Mısır matematiğinden daha ileridir. Bunun bir nedeni, Sümerlerin ve ardından Babilliler, imparatorluklarını yönetmek için verimli matematiksel hesaplamalara ihtiyaç duymalarıdır.
Babillileri Mısır gibi komşularından ayıran şey, konumsal (yer değeri olan) bir sayı sistemi kullanmalarıydı. Bu tür sistemlerde bir sayının değeri hem sembolü hem de konumu ile gösterilir. Günümüzde kullandığımız sayı sistemi de birler, onlar, yüzler gibi konumlandırmalar üzerine kurulmuştur. Bu tür sistemler, hesaplamayı daha verimli hale getirir.
Buna karşılık, eski Mısırlılar birler, onlar, yüzler, binler gibi basamakları göstermek için ayrı semboller kullandılar ve herhangi bir basamak değeri sistemine sahip değildiler. Büyük sayıları temsil etmek için 50 veya daha fazla hiyeroglif gerekiyordu ve bu hiç de pratik değildi.
60’lık Sayma Sistemi

Mezopotamyalıların sayı sistemi, neden seçtiklerine dair kesin bir bilgi bulunmamasına rağmen, 60 tabanlı bir sayı sistemidir. Neden 60’ı sayı tabanı olarak kullandıkları hala kesin olarak bilinmiyor. Diğer birçok sayıya (1, 2, 3, 4, 5, 6, 10, 12, 15, 20 ve 30) bölünebildiği için seçmiş olabilirler.
Mezopotamya’da birçok bilimsel ve matematiksel keşif yapılmıştı. Örneğin, trigonometrinin en eski kanıtı 3.700 yıllık bir Babil tabletinde yer alır. Son zamanlarda yapılan araştırmalar, eski Babillilerin ilkel bir matematik formu keşfettiğini ve bunu Jüpiter’in hareketini izlemek için kullandığını ortaya çıkardı. Babil matematiği hakkında daha fazla bilgi edinmek isterseniz bu yazımıza göz atmalısınız: Babil Matematiğinde Karşımıza Çıkan İlginç Hesaplama Yöntemleri
Kaynaklar ve ileri okumalar:
- Ancient mathematical sources; https://www.britannica.com/
- Ancient Egyptian mathematics; https://en.wikipedia.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel



