Bazı kişilerin adlarını ortaya koydukları eserler neticesinde yüzyıllar veya bin yıllar sonra da hatırlarız. Böyle iki kişi de İskoç antikacı ve arkeolog Alexander Henry Rhind ve Mısırlı yazar Ahmes olarak bilinmektedir. Bu kişilerin adları da günümüzde bir papirüste yaşıyor.
Aşağıda bir parçasını gördüğünüz bu papirüs Rhind veya Ahmes papirüsü olarak isimlendiriliyor. Önemi ise Mısır matematiği, özellikle Mısırlıların kesirleri dahiyane kullanma yöntemi hakkında bilgi vermesi. Bu yazımızda biz de bu konuyu biraz daha yakından ele alacağız. Ardından da bir çoğumuzun aşina olduğu Horus’un gözü sembolü ile ilgisini anlamaya çalışacağız.

Sistemli matematiğin doğuşu hakkında kesin bir şey söylemek mümkün değildir. Ancak yine de bulgular bize yaklaşık M.Ö 3000 –2000 yılları civarında Mısır ve Mezopotamya bölgesini işaret eder. Gelişmiş bir sayı sistemi kullandığı bilinen ilk insanlar, günümüz Irak’ında Dicle ve Fırat nehirleri arasında bulunan adına Mezopotamya dediğimiz bölgede yaşayan Sümerlerdi. Ancak aynı dönemlerde Mısır’da da matematiğin temelleri atılıyordu.
Mısır Matematiği Hakkında Neler Biliyoruz?
Matematik, antik dünyada ilerleme için önemli bir itici güçtü. Onsuz bir toplum vergi toplayamaz, ürün kayıtlarını tutamaz veya piramitler gibi mimari harikalar tasarlayamazdı. Mısırlılar arazi ölçümleri, hasat verimi tahmini, vergilendirme gibi şeyleri doğru biçimde hesaplamak için geometri, cebir ve aritmetik kullandılar.
Pisagor, Öklid, Arşimet gibi Yunan düşünürler, modern matematiğin kurucularından kabul edilir. Ama aslında, o zamanlar bu parlak beyinler firavunların ülkesinde uzun süredir devam eden hesaplama geleneklerinin ayrıntıları üzerinde çalışıyorlardı. Pisagor, adıyla anılan teoremini Mısırlıların 1400 yıl önce formüle ettiği kurallara göre düzenlemişti. Arşimet’in aktardığı, bir kürenin hacminin bir silindirin üçte ikisi olduğu bilgisi onun zamanından 1500 yıl önce Mısırlılar tarafından bulunmuştu.

MÖ dördüncü bin yılın sonunda Mısırlıların kendi sayma sistemleri vardı. Bu sistem günümüzde kullandığımız onluk sisteme benziyordu. Ancak günümüzde kullandığımız rakamlar yerine 7 farklı sembol kullanıyorlardı. Her sembolün rakamsal bir karşılığı vardı. Bu sembolleri büyükten küçüğe sıralayarak da sayıları yazabiliyorlardı.

Mısırlılar teorik olarak sadece yedi farklı sembol ile 9.999.999’a kadar herhangi bir sayıyı yazmayı başardılar. Ancak yazıkları şey bazen çok fazla sembol içermek zorundaydı. Örneğin 1.000.000 yazmak için 9 düz çizgi, 9 at nalı, 9 çengel diye devam ederek toplamda 54 karakter çizilmeliydi. Sonunda, buna çare olarak da alternatif bir sistem geliştirdiler. Hiyeratik yazı olarak bilinen bu sistem daha fazla sembole sahipti. Bu sayede büyük sayıları yazmak için daha az sembol yeterliydi.
Mısır Matematiği Birim Kesirler Üzerine Kuruluydu
Mısır matematiğinin temelinde gündelik olaylara çözümler üretmek yer alıyordu. Şimdi gündelik bir sorun düşünelim. 5 kişiye 3 somun ekmeğin paylaştırılması gibi içinden çıkılamaz bir durumu düşünün. Mısırlıların bu sorunu çözmek için kullandıkları yöntem şu idi.
5 ekmeğin önce 2 tanesini al ve 3 eşit parçaya böl. Üçüncü ekmeği de 5 eşit parçaya böl. Önce herkese üçte birlik parçalardan ve beşte birlik parçalardan birer tane ver. Geriye bir tane üçte birlik parça kalacaktır. Şimdi bu parçayı da beşe böl. Yani 15’te birlik bir parça ekmek elde et. Son parçayı da kişilere dağıtınca adil bir çözüm bulunmuş olacaktır.
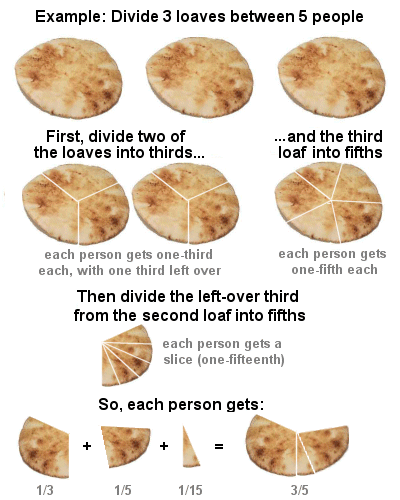
Aslında Mısır matematiğinin en önemli tarafı kesirlerle yapılan hesaplamalardır. Bütün kesirler payı bir olan ve birim kesir denilen kesirlerin toplamı şeklinde yazılabiliyordu. Bunlara Mısır kesirleri de denilmektedir. Birim kesirler yazım kolaylığı açısından paydadaki sayının üzerine bir çizgi çekilerek ifade ediliyordu.
Birim kesirler dışında müsaade edilen tek kesir 2/3’tü. Bunun neden kullanıldığı ile ilgili kesin bir bilgi ne yazık ki yoktur. Aşağıda bir kaç örnek görebilirsiniz. Mısır kesirlerini oluşturmak kolay değildir. Zaten yazının başında aktardığımız Rhind papirüsü biraz da bu nedenle kaleme alınmıştır.
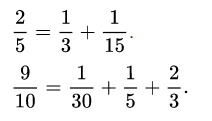
Antik Mısır Çarpımı Nasıl Yapılıyordu?
Mısırlılar toplama ve çıkarmada, bugün bizim kullandığımız metotları kullanmışlardır. Mısır aritmetiğinin en ilginç yanı çarpma işlemidir. Çarpmanız gereken iki sayıyı aralarında biraz boşluk kalacak biçimde yazın. Birinci çarpanın altına 1, ikinci çarpanın altına da çarpanın kendisini yazarak başlayın. Şimdi her iki sütunda tepedeki sayıyı iki ile çarpın ( ya da kendisi ile toplayın) ve yeni bir satır elde edin.
Şu anda birinci sütununuz ikinin kuvvetlerinden oluşuyor. Bu biçimde birinci çarpanı geçmeyen ilk sayıyı bulun ve durun. Aşağıdaki örneğe dikkat edelim. ( 64’te işlemi durdurduk. Çünkü bir sonraki sayı olan 128, ilk çarpanımız olan 85’i geçer.) Ancak aşağıdaki çarpmada bazı sayıların kırmızı ile işaretlendiğine dikkat edin.

Kırmızı işaretli olanlara dikkat edin demiştik. Çünkü bu sayıların toplamı yandaki biçimdedir. 85 = 1 + 4 + 16 + 64. Bu da aslında 85 sayısının 2’lik sistemdeki karşılığıdır. 85 = 10101012 . Rhind papirüsüne göre bu kuvvetler şu şekilde bulunur. 85 – 64 = 21.
21’in altındaki 2’nin en büyük kuvvetini bulun: 16. Şimdi 21 – 16 = 5’i hesaplayın ve 5’in altındaki 2’nin en büyük kuvvetini bulun: 4. Şimdi 5 – 4 = 1’i hesaplayın ve sonucun 1 olduğunu gözlemleyin. Bu noktadan sonra yapılması gereken şey bu sayıların bulunduğu satırları silmek ve geriye kalan ikinci sütundaki sayıları toplamak olacaktır. Sonucu aşağıda görebilirsiniz.

Horus’un Gözü Hangi Anlamı Taşıyordu?

Horus, Eski Mısır dininde bir gözü ay, bir gözü Güneş olan şahin biçimindeki Tanrı’nın adıdır. Firavunlar kendilerini Horus’un yeryüzündeki cisimleşmiş halleri olarak gördükleri için Mısır’ın, Ra ile birlikte en önemli tanrılarından biridir.
Mitolojiye göre Horus efsanesi şöyledir. Horus’un babası Osiris, kardeşi Seth tarafından öldürülünce, Horus babasının intikamını almaya karar verir. Seth, Horus’la savaşırken gözünü çıkarır. Tanrılar Horus’un yanında yer alır. Sonrasında da dağılmış olan gözü tekrar birleştirirler. Ancak bir araya getirilse de göz eksik kalır. Bu eksiklik büyü gücü ile tamamlanır ve böylece göz eskisi gibi olur.
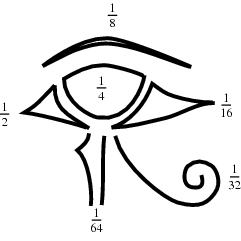
Horus’un Gözü önemli bir eski Mısır sembolüydü. Yukarıda aktardığımız efsane kısmıydı. Mısırlılar bu efsaneyi pratiğe dökmüşlerdi. Sembolü oluşturan parçalar bir hacim ölüm birimi olan hekatın belli oranlarını ifade ediyordu. Horus’un Gözü tam bir hekat’ı temsil ediyorsa, onu oluşturmak için birleştirilen altı parça kesir gerekiyordu. 1/2, 1/4, 1/8, 1/16, 1/32 ve 1/64.
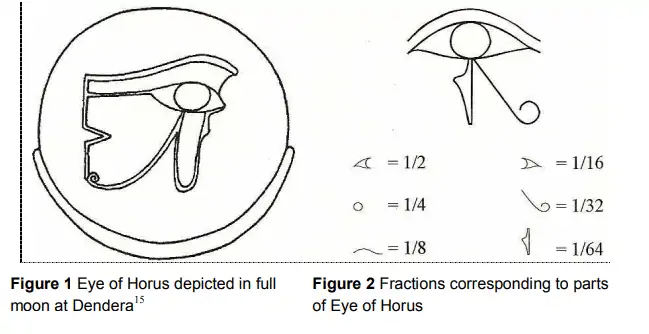
şeklinde yorumladığı altı bölümden oluşuyordu
Mısır kesirleri pratik amaçlar ile kullanılıyordu ama buldukları çözüm yolları gerçekten etkileyici.
Kaynaklar ve ileri okumalar
- Eye of Horus; Bağlantı: https://en.wikipedia.org/wiki/Eye_of_Horus
- This well-known Egyptian symbol is actually an early math problem; Yayınlanma tarihi: 5 Temmuz 2012; Bağlantı: http://io9.gizmodo.com/
- Egyptian Multiplication; Bağlantı: https://www.cut-the-knot.org
Matematiksel