Eminiz ki her matematik öğrencisinin aklından geçen şeylerden bir tanesi, tahtada sadece anlamsız şekiller olarak gördüğü bir ispata bakıp, “peki ama bu ispata ne gerek var? “sorusunu sormaktır. Sonuçta tahtada yazılı olanlar sadece profesyonel bir matematikçinin anlayabileceği ezoterik, teknik yazılar gibi görünmektedir. Oysa ki matematikte ispatın önemi çok büyüktür. İspatlanmayan bir ifade (aksiyom değil ise) matematikçiler tarafından doğru kabul edilemez.
İspat, bir ifadenin doğru olduğunu göstermeye çalışan mantıksal bir argümandır. Matematikte ve bilgisayar biliminde, bir ispatın kabul edilmeden önce iyi düşünülmesi ve test edilmesi gerekir. Ancak o zaman bile, bir ispatın yanlış olduğu keşfedilebilir. Bir şeyi ispatlamanın birçok farklı yolu vardır. Bu yazıda belli başlı bir kaç tanesini ele alacağız.
Doğrudan İspat Yöntemleri
Doğrudan ispat yöntemleri, ispat yaparken çoğunlukla öğrencilerin aklına ilk gelen ispat yöntemleridir. Bu yöntemler genellikle koşullu önermelerin (p ⇒ q) kanıtında kullanılırlar. Koşullu önermeleri ispatlarken varsayımı/hipotezi (p) doğru kabul ederiz ve daha önceden doğruluğu kanıtlanmış teoremleri veya ispatları kullanarak sonuca (q) ulaşmaya çalışırız.

Örneğin, “İki çift sayının toplamı çifttir” önermesini düşünelim. Öncelikle önermemizi şöyle yazalım. ‘Eğer a ve b çift sayılar ise a+b bir çift sayıdır. Bu şekilde yazdığımızda önermemiz koşullu olduğu daha belirgin hale gelir.
Bu durumda p: a ve b çift sayılardır ve q: a+b bir çift sayıdır biçiminde olacaktır. Şimdi ispatımıza geçelim. Koşullu önermedeki hipotez kısmını doğru kabul edelim, yani a ve b birer çift sayı olsun. Şimdi de çift sayının tanımını hatırlayarak şunu yazabiliriz. a ve b birer çift sayı olduğu için öyle k ve t sayıları vardır ki a=2k ve b=2t eşitliklerini sağlasınlar. O zaman a+b=2k+2t=2(k+t) olur. m=k+t olsun. Buradan da a+b=2m olur demek ki a+b sayısı çift sayıdır.
Durum Analizli İspat
Durum analizli ispat, bir nevi ispatımızı kolaylaştırmanın bir yoludur. Eğer ispatlamamız gereken önerme birden fazla durum içeriyorsa, bu durumları parçalara ayırarak bunları ayrı ayrı ispatlarız. Örneğin, “1+(2n-1)(-1)n ifadesi bütün n tamsayıları için 4’ün bir katıdır.” önermesini ele alalım. Şimdi buradaki (-1)n ifadesine dikkat edelim. Bu ifade, n tek bir sayı iken negatif, çift bir sayı iken ise pozitif bir sayıdır. O zaman bu önermeyi aşağıdaki şekilde iki duruma ayırabiliriz.
1. Durum: n bir çift tam sayı olsun. O zaman k herhangi bir tamsayı olmak üzere n=2k diyebiliriz. Bu da bizim ifademizi şu hale sokar: 1+(4k-1)(-1)2k=1+(4k-1)=4k. Buradan da bu durum için önermemizi ispatlamış oluruz.
2. Durum: n bir tek tam sayı olsun. Benzer bir şekilde k herhangi bir tamsayı olmak üzere n.=2k+1 diyebiliriz. O zaman ifademiz şu hale gelir: 1+(-1)2k+1(4k+2-1)=1+(-1)(4k+1)=-4k. Buradan da bu durumu da kanıtlamış oluruz. Ve de ispatımızı da bitirmiş oluruz.
Dolaylı İspat Yöntemleri

İki tane dolaylı ispat metodu vardır. Bunlar: karşıt ters metodu ve olmayana ergi metodudur.
Karşıt Ters Metodu
Sadece koşullu önermelerin ve ancak ve ancak önermelerinin karşıt tersi alınabilir. Bir önermenin karşıt tersi o önermeden elde edilen ve aynı doğruluk değerine sahip olan başka bir önermedir. Karşıt ters metodu, bir önermenin normal halini ispatlamak çok kolay olmadığında kullanılan bir metottur.
Örneğin ” x bir tam sayı olsun. Eğer 7x+5 bir tek tamsayı ise x bir çift tamsayıdır.” önermesine bakalım. Burada p: 7x+5 bir tek tamsayıdır. Ve q: x bir çift tamsayıdır biçiminde düşünebiliriz. Şimdi bu önermeyi ispatlamak yerine karşıt tersini ispatlayalım.
¬p: 7x+5 bir çift tamsayıdır. ¬q: x bir tek tamsayıdır. ¬q ⇒ ¬p: Eğer x bir tek tamsayı ise 7x+5 bir çift tamsayıdır. Burada sonrasını ise doğrudan ispat yöntemini kullanarak kanıtlayacağız. Önermenin hipotez kısmını (¬q) doğru kabul edelim. O zaman şöyle diyebiliriz . Öyle bir k tamsayısı vardır ki x=2k+1 olsun. Buradan şu sonuç çıkar: 7x+5=7(2k+1)+5=14k+12=2(7k+6). Görülebileceği gibi 7x+5 bir çift tamsayıdır. Önermemizin karşıt tersi doğru olduğu için direkt olarak önermemiz de doğrudur diyebiliriz.

Olmayana Ergi Yöntemi
Gelelim en popüler ispat metotlarından birine: olmayana ergi. Bu yöntemin popüler olma sebeplerinden birisi de Öklid’in bu metodu asal sayıların sonsuzluğunu ispatlarken kullanmasıdır. Olmayana ergi yöntemi neredeyse her çeşit önermelerde kullanılabilir.
Bu yöntem sadece koşullu önerme ispatlarıyla sınırlı değildir, herhangi çeşit bir önermenin ispatında kullanılabilir. Buradaki temel fikir, kanıtlanmak istenilen önermenin yanlış olduğunu kabul edip, bunun bir çelişkiye yol açtığını göstermektir. Buna göre, yapılan varsayımın yanlış olduğu sonucuna varacağımız için, önerme doğru olmak zorundadır. Örneğin, “Eğer a2 çift sayı ise a çifttir.” önermesini ele alalım.
Bu koşullu önermenin ispatında yukarıda bahsettiğimiz gibi önermenin sonuç kısmını yanlış kabul edeceğiz. Ve de aynı doğrudan ispat yaparmış gibi önermemizin hipotez kısmını doğru kabul edeceğiz. Yani hem a tek sayıdır hem de a2 çift sayıdır diye kabul edeceğiz. Demek ki öyle bir k tam sayısı vardır ki a=2k+1. Buradan da a2=(2k+1)2=4k2+4k+1=2(2k2+2k)+1 çıkar yani a2 bir tek sayıdır. Fakat biz a2’nin çift sayı olduğunu kabul etmiştik. Bu bir çelişkidir. Demek ki a bir çift sayıymış.
Olmayana ergi güçlü bir ispat yöntemi olmasına rağmen bu yöntemi, doğrudan veya dolaylı ispat yöntemleri kullanılamaz gibi göründüğünde kullanmak en iyisidir. Bunun nedeni olmayana ergi yöntemi, içerisinde gizli bir basit dolaylı ispat barındırıyor olabilir. Bu durumda daha basit olan yaklaşım ile devam etmek en doğrusudur.

Tümevarım
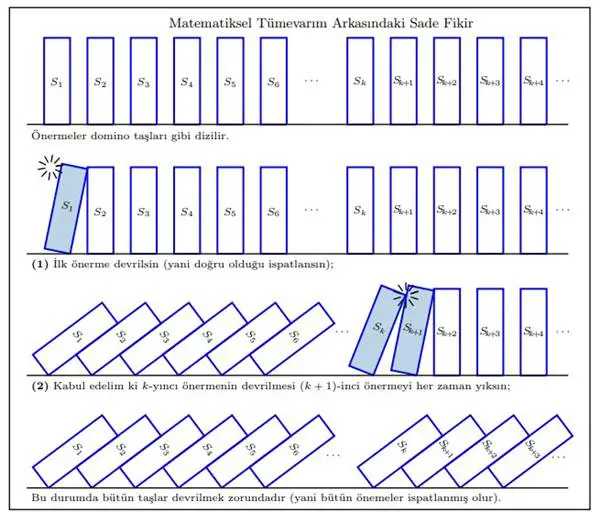
Bir diğer popüler ispat metodu ise tümevarımla ispattır. Tümevarımla ispat yöntemini domino taşlarının devrilmesine benzetebiliriz. Tümevarım ispatında iki çok önemli adım vardır, bunlar: başlangıç adımı ve tümevarım adımıdır. Yine domino benzetmesinden yola çıkarsak, başlangıç adımını kişinin en baştaki domino taşını itmesine ve tümevarım adımını da her bir taşın bir sonraki taşı devireceği garantisine benzetebiliriz.
Örneğin “İlk n tek doğal sayının toplamı n2 olur” önermesini ele alalım. Bu sanıda verilen ifade aşağıdaki tabloda görselleştirilmiştir. Tablonun her satırı n doğal sayısı ile başlar ve bunu ilk n tane tek doğal sayının toplamı takip eder. Her satır n2 ile biter.

Tablonun ilk beş satırına dikkatlice bakılırsa gerçekten de bu satırlardaki ilk n tek doğal sayının toplamı n2 olur. Üstelik ilk beş satır, n´inci sıradaki tek doğal sayının (her toplamdaki son sayı) 2n – 1 olduğuna işaret eder. Bu tablo şu soruyu akla getirir: 1+ 3+5+7+9+…+2n-1 toplamı her zaman gerçekten de n2 midir?
Matematiksel tümevarım, bu tipteki soruları cevaplamak için dizayn edilmiştir. Bu yöntem S1, S2, S3, . . . , Sn, . . . önermelerinden oluşan bir kümedeki bütün önermelerin doğru olduğunu ispatlamak için kullanılır. Bu metot gerçekten de çok sadedir. Kullanışlılığı da sadeliğinden gelir.
Bu yazımızda sizlere tanıttığımız ispat yöntemleri en popüler olanlar arasından seçilmişti. Başta da dediğimiz gibi aslında bir çok ispat yöntemi vardır ve hepsini tek bir yazıda ele almak imkansızdır. Detaylı bir araştırma yapıyorsanız yazının devamında bu kitaptaki ispat yöntemlerini incelemenizi öneririz.
Yazının bitiminde güzel bir ispata göz atmak isterseniz: Öklid’in Asal Sayıların Sonsuzluğuna Dair İspatı
Matematiksel








Yazmayı düşündüğüm yazıları biri yazınca hem bozuluyorum hem de biraz seviniyorum. Elinize sağlık, güzel olmuş.
Çok teşekkür ederim :)