Canınız sıkılıp bir tükenmez kalemi parçalara ayırmayı denediyseniz mutlaka içindeki yay ile oynamışsınızdır. Bir yayı sıkıştırıp gevşetmek eğlencelidir ancak belli bir noktadan sonra yay işlevini kaybeder. Bu andan sonra da onu eski şekline döndürmek için yapılan tüm girişimler boş olacaktır. Tükenmez kalemlerdeki yaylar, Hooke Yasasına verilecek en basit örneklerden birisidir.

Yaylar, insan mühendisliğinin ve yaratıcılığının önemli bir göstergesidir. Basma yayı, çekme yayı, burulma yayı, sarmal yayı gibi pek çok farklı türü bulunur ve her biri kendine özgü bir işlevi yerine getirir. Bu çeşitlilik, insanların birçok farklı araç ve mekanizma geliştirmesini mümkün kılmıştır. Yayların sağladığı olanaklar, özellikle 17. yüzyılın sonları ve 18. yüzyıldaki Bilim Devrimi sırasında hayatımıza giren pek çok icadın temelinde yer alır.
Yaylar, mekanik enerji depolamak için kullanılan elastik yapılar oldukları için oldukça geniş bir kullanım alanına sahiptir. Tarih boyunca geliştirilen pek çok icatta olduğu gibi, yayların da bu kadar yaygın kullanılabilmesi için temel mekanik prensiplerin anlaşılması şarttı. Yaylarda elastikiyet, burulma ve kuvvet yasalarının birleşimi Hooke Yasası olarak bilinmektedir.

Hooke Yasası Nedir?
İngiliz fizikçi ve bilim insanı Robert Hooke (1635-1703), 17. yüzyılın bilimsel devrimine önemli katkılarda bulunmuştur. 1665 yılında yayımladığı Micrographia adlı eser, bilim dünyasında büyük yankı uyandırdı ve tarihin ilk çok satan bilim kitaplarından biri oldu.
Hooke, ayrıca ilk Gregoryen yansıtmalı teleskobu yaparak önemli astronomik gözlemler gerçekleştirdi. Gezegenlerin hareketlerini matematiksel olarak tanımladı. Tüm bunlara ek olarak, bugün kendi adıyla anılan ve esnekliğin temel prensiplerini açıklayan Hooke Yasası’nı da keşfetti.

Hooke Yasası aslında, Robert Hooke’un saatlere olan ilgisinin bir sonucu olarak ortaya çıktı. O dönemde kullanılan saatler genellikle sarkaçlıydı. Ancak sarkaçlı saatlerin önemli bir sorunu vardı: Seyir halindeki gemilerde doğru çalışmıyorlardı.
Dalgalı denizlerde sarkaçların sabit kalması mümkün olmadığından, gemilerde zamanı doğru ölçmek çok zordu. Oysa zamanı doğru ölçebilmek, gemilerin boylamı hesaplayabilmesi ve kaybolmadan hedeflerine ulaşabilmesi için hayati öneme sahipti.
Hooke, eğer bir sarkaç yerine bir yay kullanarak saat yaparsa, denizde zaman ölçme sorununu çözeceğini düşündü. Yay kullanmak, aynı zamanda cebe sığacak kadar küçük saatler üretmenin de önünü açacaktı.
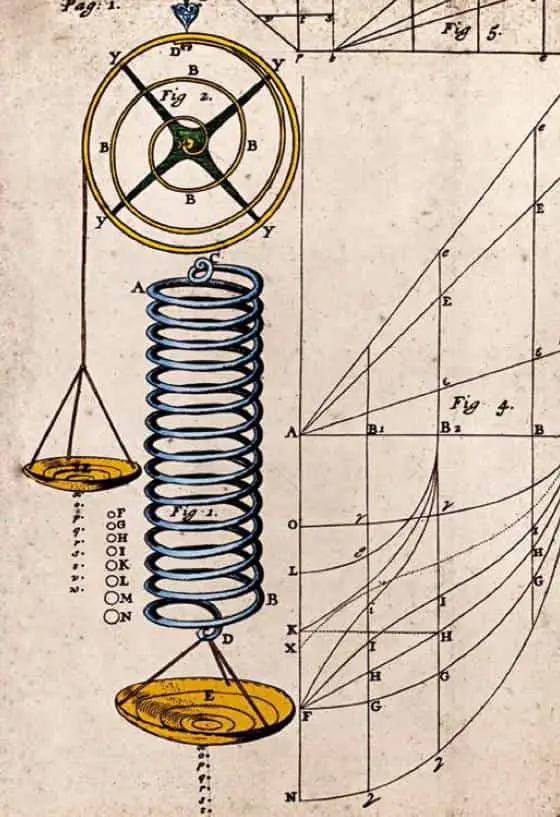
1670’lerde Hooke, Hollandalı bilim insanı Christiaan Huygens’in de yaylı bir saat üzerinde çalıştığını duydu. İkinci sırada kalmamak için hızla harekete geçti ve ünlü saatçi Thomas Tompion ile iş birliği yapmaya başladı. Bu süreçte yaylar üzerinde çeşitli deneyler yaptı. Yaptığı deneyler sonucunda, bugün Hooke Yasası olarak bildiğimiz basit ama önemli ilişkiyi keşfetti.
Bu bağıntıyı 1660 yılında Latince bir anagramla gizlice ifade etti. Çözümünü ise 1678’de yayımladı: ut tensio, sic vis. Bu ifade, “uzama ne kadarsa kuvvet de o kadar” ya da “uzama kuvvetle doğru orantılıdır” anlamına gelir.
Hooke Yasasının Uygulamaları
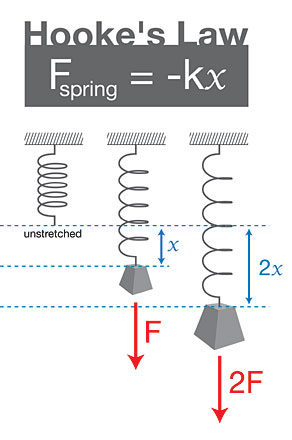
Hooke Yasası, bir yayın ne kadar sıkıştırıldığı ya da gerildiği ile uygulanan kuvvetin doğru orantılı olduğunu söyler. Yani uygulanan kuvveti iki katına çıkarırsanız, yay da iki kat daha fazla uzar. Bu ilişki, basit bir denklemle gösterilir: F = kx. Burada F uygulanan kuvveti, x yayın uzama ya da sıkışma miktarını, k ise yayın sabitini gösterir. Denklemdeki eksi işareti, yayın geri çağırıcı kuvvetinin, uzama veya sıkışma yönüne zıt olduğunu belirtir.
Hooke Yasası, elastikiyetin ilk klasik açıklamalarından biridir. Elastikiyet, bir nesnenin şekli bozulduktan sonra eski haline dönebilme özelliğidir. Bu geri dönme isteğine “geri çağırıcı kuvvet” denir. Hooke Yasası’na göre, bu kuvvet genellikle nesnenin yaşadığı uzama miktarıyla orantılıdır.
Hooke Yasası, yayların davranışını açıklamanın yanı sıra, elastik bir cismin deforme olduğu birçok durumda da geçerlidir. Bu durumlar arasında balon şişirmekten lastik bant çekmeye, hatta yüksek bir binanın rüzgarla ne kadar eğilip sallanacağını ölçmeye kadar pek çok örnek bulunur.
Hooke Yasası, birçok önemli pratik uygulamaya yol açtı. Ayrıca, deformasyon kuvvetleri yeterince küçük olduğu sürece tüm katı cisimlerin davranışını iyi şekilde açıklayabildiği için, birçok bilim ve mühendislik dalı da Hooke’a minnettardır. Bu alanlar arasında sismoloji, moleküler mekanik ve akustik gibi disiplinler yer alır.
Ancak diğer klasik mekanik yasaları gibi, Hooke Yasası da yalnızca sınırlı bir çerçevede geçerlidir. Hiçbir malzeme, belli bir minimum boyutun altına sıkıştırılamaz veya maksimum boyutun ötesine gerilemez. Aksi halde kalıcı bir deformasyon veya hal değişimi meydana gelir.
Bu yüzden, Hooke Yasası sadece sınırlı kuvvetler veya küçük deformasyonlar için geçerlidir. Hatta pek çok malzeme, elastik sınırlarına ulaşmadan önce bile Hooke Yasası’ndan belirgin şekilde sapmaya başlar. Yine de genel formuyla Hooke Yasası, Newton’un statik denge yasalarıyla uyumludur. Bu iki temel prensip birlikte kullanıldığında, karmaşık cisimlerde gerilme ve şekil değiştirme arasındaki ilişkiyi, cismin yapıldığı malzemenin özelliklerine bağlı olarak açıklamak mümkün olur.
Günümüzde Hooke Yasası
Modern elastikiyet teorisi, Hooke Yasası’nın daha genel bir yorumudur. Bu teori, elastik bir nesne veya malzemedeki şekil değişiminin (deformasyonun), uygulanan gerilme (stres) ile orantılı olduğunu söyler. Ancak, genel gerilme ve deformasyonlar birden fazla bağımsız bileşene sahip olabileceği için, bu “orantı katsayısı” artık tek bir sayıdan ibaret olmaz.
Buna iyi bir örnek, rüzgar etkisinde görülür. Rüzgarın uyguladığı gerilme, hem şiddet hem de yön bakımından değişkenlik gösterir. Böyle durumlarda, orantıyı tek bir değerle ifade etmek yerine, gerçek sayılardan oluşan bir matrisle gösterilen bir lineer harita (yani bir tensör) kullanmak en doğru yaklaşımdır.
Kaynaklar ve İleri Okumalar:
- What is Hooke’s Law?; Yayınlanma tarihi: 16 Şubat 2015; Bağlantı: https://phys.org
- The Physics Book; Dorling Kindersley Limited; DK Publishing; 2020
- The Editors of Encyclopaedia Britannica. “Hooke’s law”. Encyclopedia Britannica, 26 Apr. 2025, https://www.britannica.com/science/Hookes-law. Accessed 28 April 2025.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel