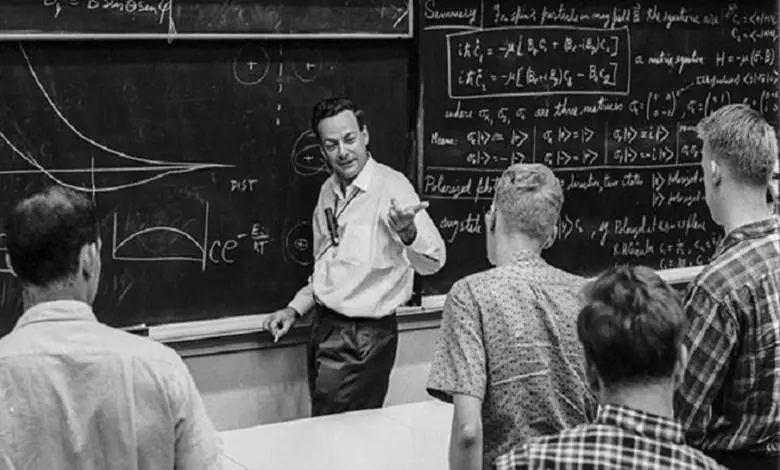
Fizikçi denildiğinde çoğumuzun aklına ilk olarak Einstein gelir. İkinci olarak da gelen isim genellikle Hawking veya Newton olur. Çok azımız Richard Feynman adını, onun fizik bilimine katkılarını biliriz. Oysa ki Feynman 20. yüzyılın en önemli fizikçilerinden ve tarihin gördüğü en büyük dehalardan biri olarak kabul edilmektedir.
Kendisi temel parçacıkların birbiriyle etkileşimlerini tanımlayan kuantum mekaniği ve kuantum elektrodinamiğine önemli katkılarda bulunmuştur. Bunun sonucunda da, Feynman 1965 yılında Sin-Itiro Tomonaga ve Julian Schwinger ile birlikte Nobel Ödülünü kazanmıştır.
Richard Feynman, çalışmalarını yalnızca teorik fizik alanında yayınlamış olsaydı muhtemelen adı yine de fazla hatırlanmayabilirdi. Ancak ders kitaplarının ölümünden 30 yıl sonra bile, çok satanlar arasında bulunmasının nedeni sadece fizik üzerine yaptığı çalışmalar değildir.
Richard Feynman, kendine özgü anlatım biçimi ile fiziğin kitlelere ulaşmasında önemli bir rol oynamıştır. Bu yazıda en sevilen Feynman kitaplarından bazılarına kısaca göz atalım.
“Eminim Şaka Yapıyorsunuz Bay Feynman!” Meraklı Bir Karakterin Serüvenleri

Sadece bir Feynman kitabı okuyacak vaktiniz varsa, bu kitap doğru seçim olacaktır. Orijinal adı “Surely You’re Joking Mr. Feynman!” olan ve 1985 yılında yayınlanan bu kitap, New York Times Bestseller listesinde yer almış ve 500.000’den fazla satmıştır.
Richard Feynman aykırı serüvenleriyle de tanınmıştır. Kitap onun hem komik hem de düşündürücü hayatından bölümleri ele almaktadır. Kendisi kasaların şifrelerini kırmaktan çetelerle takılmaya, samba müziği yapan bir grupta bongo çalmaktan takma isim altında sergiler açan amatör bir ressamlığa kadar dolu bir hayat yaşamıştır.
Bu kitapta onun bu serüvenlerine eşlik edeceksiniz. Aynı zamanda, kuantum fiziğinin gizemlerinden barda kızlara içki ısmarlamanın kurallarını keşfedişine kadar pek çok hayrete düşürücü olayı onun dilinden okuyabilirsiniz.
Keşfetmenin Hazzı

Bu kitabın yazarı Richard Feynman değildir. Jeffrey Robbins tarafından düzenlenen bu kitap çoğunlukla yazıya dökülmüş konuşmalardan ve röportajlardan oluşuyor. Feynman’ın düşünceleri ve yaşamı konusunda önemli ipuçları veren kitapta Feynman, bilimin ne olduğundan keşfetmenin sihirli dünyasına ve bilim ile din arasındaki ilişkiye kadar pek çok konuyu, kendine has tarzıyla yorumluyor.
Nobel Ödülü’nü kazandığında Feynman şunu söylemiştir: “Ödülümü zaten aldım… ödül, bir şeyi bulmaktan duyulan haz, keşfetmenin verdiği heyecan ve diğer insanların bunu görmesidir, ki bunlar gerçek şeylerdir.” Feynman’ın bilim için hissettiği tutkuyu kısa çalışmalarının toplandığı bu kitaptan daha iyi gösteren başka bir kaynak yoktur.
Fizik Yasaları Üzerine

Fizik Yasaları Üzerine ya da özgün adıyla The Character of Physical Law (1964) kitabı, Feynman’ın davetli olarak geldiği Amerika Birleşik Devletleri’nin Cornell Üniversitesi’nde verdiği bir dizi konferansı kapsar. Feynman, fiziğin geniş dünyasını, bir Marslıyla yapılan hayali telefon konuşması benzeri örneklerle, fiziği fizikçi olmayanlar için de çekici kılan bir dil ile okurlarına tanıtır. Kitap çok az sayıda diyagram ve denklem içerir. Bu da kitabın kolayca anlaşılmasını sağlamaktadır.
Başkalarının Ne Düşündüğünden Sana Ne

Ralph Leighton tarafından derlenen Başkalarının Ne Düşündüğünden Sana Ne, Feynman’ın çok ilgi gören biyografisi Eminim Saka Yapıyorsunuz, Bay Feynman’ın devamı niteliğinde. Ancak Feynman bu kitapta çoğunlukla şaka yapmıyor.
Ayrıca bu kitapta konular, Eminim Saka Yapıyorsunuz Bay Feynman’a göre birbirleriyle daha az ilgili. Kitaptaki “Bay Feynman Washington’a gidiyor” bölümü Feynman’ın uzay mekiği Challenger1 m patlayışını araştıran Rogers Komisyonu’ndaki maceralarını kapsıyor.
Feynman’ın en dokunaklı ve ilham verici konuşmalarından biri olan “Bilimin Değeri” kitabın Sonsöz’ü. Okumak isterseniz: Bilimin Değerini Richard Feynman Anlatsın
Altı Kolay Parça

Bu kitap, Feynman’ın 1961-1963 arası Caltech’te üniversite birinci ve ikinci sınıf öğrencilerine verdiği fizik derslerinin özetleridir. Temel fizik, atom kuramı, enerji, kütleçekim, kuantum ve fizikle diğer bilimlerin ortak noktalarını kapsayan bu konular, Feynman’ın usta anlatımıyla fizik bilmeyen okurların anlayabileceği düzeyde sunulmaktadır.
Feynman’ın etkili bir öğretmen olarak ün kazanması, bu kitapta olduğu gibi, teknik ve matematiksel dili en az seviyede kullanarak fiziksel ilkeleri anlatabilme yeteneğindendir. Altı Kolay Parça fizikteki konuların sistematik bir özeti olmaktansa, fizikteki farklı konulara çok iyi bir rehber eşliğinde çıkılmış bir gezintiye benziyor.
Feynman gibi önemli bir fizikçinin evreni yorumlayış biçimini görmek ve kuantum mekaniği gibi modern fizik kuramları hakkında bilgi edinmek için Altı Kolay Parça genel okuyucu için eşsiz bir ilk kaynaktır.
Feynman’ın ayrıca Altı Kolay Parça’dan farklı olarak bir parça daha fazla matematik içeren Altı Zor Parça isimli bir kitabı daha vardır. Ayrıca göz atmak isterseniz: Feynman Tekniği İle Yeni Bir Bilgi Kolayca Nasıl Öğrenilir?
Kaynak: Top 5 Richard Feynman books; https://www.sciencefocus.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel