Algoritmalar dijital çağda her yerdedir. Buna karşın çoğu kişi, onların bilgisayarlardan binlerce yıl önce ortaya çıktığını ve matematiğin özüne uzandığını fark etmez. Oysa ki algoritmalar çağı Öklid algoritması ile başlamıştır.

Matematiğin Antik Yunan’daki doğuşu, ilk algoritmalardan birinin geliştirilmesiyle çakışır. Öklid’in Elemanlar adlı eserinde, asal sayıların sonsuzluğuna dair kanıtın yanında, belirli bir problemi çözmeye yönelik adım adım bir yöntem de yer alır. İki tam sayı verildiğinde, bu yöntemi izleyen herkes her ikisini de bölen en büyük tam sayıyı ( en büyük ortak böleni – EBOB) kolayca bulur.
Otuz altı birim uzunluğunda ve on beş birim genişliğinde bir zemini kaplamak istediğinizi varsayın. Zemini boşluk ya da taşma olmadan döşeyecek en büyük kare karoların kenar uzunluğunu arıyorsunuz. Bunu nasıl bulabilirsiniz? İşte bu soruya yanıt veren, iki bin yıldan daha eski bir algoritma vardır.

Öklid Algoritması Nedir?
İki sayı alalım: M ve N. N, M’den küçük olsun. Önce M’yi N’ye böleriz ve kalanı N₁ olarak adlandırırız. Eğer kalan sıfırsa, N her iki sayıyı da bölen en büyük sayıdır. Kalan sıfır değilse, bu kez N’yi N₁’e böleriz ve yeni kalana N₂ deriz. N₂ sıfırsa, aradığımız sayı N₁’dir. Değilse, aynı işlemi sürdürürüz: N₁’i N₂’ye böler, kalanı N₃ olarak adlandırırız.
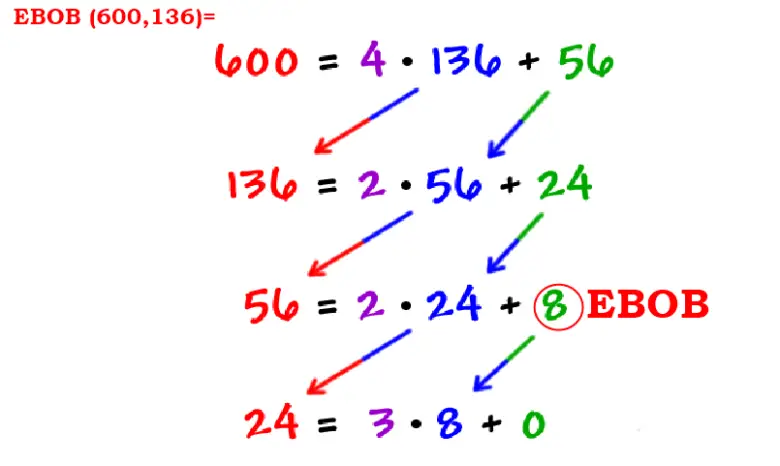
Bu işlem bu şekilde devam eder. Kalanlar her adımda küçülür ve hepsi tam sayı olduğundan süreç mutlaka sıfıra ulaşır. Sıfıra ulaşıldığında, bir önceki kalan M ve N’yi birlikte bölen en büyük sayıdır. Bu sayı, en büyük ortak bölen olacaktır.
M = 36 ve N = 15 olsun. M’yi N’ye böldüğümüzde 2 elde ederiz ve kalan N₁ = 6 olur. Ardından N’yi N₁’e böleriz. Sonuç yine 2’dir ve bu kez kalan N₂ = 3’tür. Şimdi N₁’i N₂’ye böldüğümüzde hiç kalan kalmaz. Bu da 3’ün hem 36’yı hem de 15’i bölen en büyük sayı olduğunu gösterir.
Bu süreçte çok sayıda “eğer … ise …” adımı yer alır. Bu, algoritmaların tipik bir özelliğidir ve onları kodlama ile bilgisayarlar için son derece uygun kılar. Öklid’in bu yöntemi, bir algoritmanın taşıması gereken dört temel özelliği açıkça sergiler.
- Açık, kesin ve yoruma kapalı bir talimatlar dizisinden oluşur.
- Hangi sayılar girilirse girilsin, süreç sonsuz döngüye girmez.
- Verilen her girdi için geçerli bir sonuç üretir.
- Hesaplamayı verimli ve hızlı biçimde gerçekleştirir.
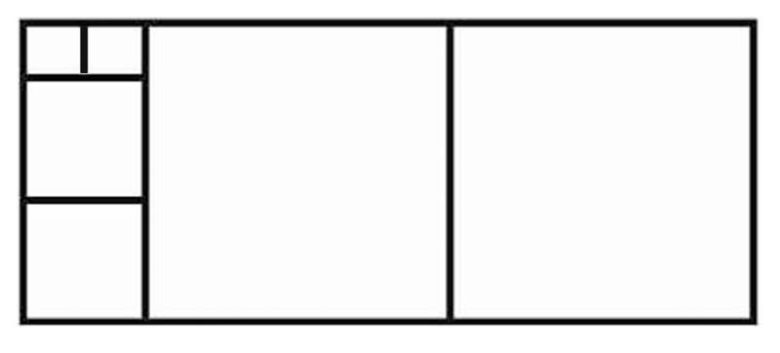
Şimdi zemin döşeme problemine geri dönelim. Önce, zeminin içine sığacak en büyük kare karoyu düşünün. Ardından geriye kalan alanın içine sığacak en büyük kareyi yerleştirin. Bu işlemi kalan alanlar için tekrarlayın. Sonunda, geriye kalan bölgeyi tam olarak kaplayan bir kareye ulaşırsınız. İşte bu karonun kenar uzunluğu, zeminin tamamını kusursuz biçimde kaplayacak en büyük kare karodur.
Öklid Algoritması Ne İşimize Yarar?
Öklid algoritmasında hiçbir aşama belirsizlik taşımaz. Her adımda kalan daha da küçülür ve bu süreç kaçınılmaz olarak sıfıra ulaşır. Kalan sıfır olduğunda algoritma durur ve sonucu üretir. Sayılar büyüdükçe işlem süresi artsa da yöntem son derece etkilidir. Hatta adım sayısı, küçük olan sayının basamak sayısının yaklaşık beş katıyla sınırlıdır.
Öklid’in Elemanlar adlı eserinde algoritmanın tüm adımları yer alır. Ancak Öklid’in kullandığı dil oldukça hantaldı. Antik Yunanlılar matematiksel problemleri geometrik olarak düşünüyordu. Sayıları farklı uzunluklarda doğru parçalarıyla ifade ediyor, kanıtları ise çizimlerle kuruyorlardı.
Bu yaklaşım, zemini karelerle kaplama örneğinde olduğu gibi görseldi. Ne var ki görseller, matematiği tam bir kesinlikle yürütmek için yeterli değildir. Bunun için, değişken sayıları harflerle temsil eden cebir diline ihtiyaç vardır.

İnternet ve akıllı telefon uygulamalarından 1000 yıldan fazla bir süre önce, İranlı bilim insanı ve bilge, tam adı ile Ebu Abdullah Muhammed Bin Musa el Harezmi (780-850) – kısaca Harezmi- modern bilime şekil veren kişilerden biri olarak tarihe adını yazdırdı.
Bağdat’taki büyük “Bilgelik Evi”nin ilk yöneticilerinden biri olan el-Hârizmî, Antik Yunan matematik metinlerinin Arapçaya çevrilmesinde önemli bir rol oynadı. Algoritma kelimesinin kökeni de onun adının Latince versiyonunda yer alan “algorithmi” kelimesinden gelmektedir. Kelime ilk olarak 1230 yılında kullanıldı.
Kaynaklar ve ileri okumalar:
- Music and Euclid’s algorithm; yayınlanma tarihi: 1 Eylül 2006; Bağlantı: https://plus.maths.org/
- John Stillwell; Elements of Mathematics: From Euclid to Gödel ; Yayıncı: Princeton University Press
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel