Monty hall problemi, matematikteki en ünlü problemlerden biridir. Problemin kaynağı da ABD televizyonlarında 1963’den 1977’ye kadar yayında kalan Let’s Make A Deal (Bizde ki Var mısın, Yok musun yarışmasının atası denilebilir) isimli bir yarışma programıdır.
Monty Hall ise bu yarışmaya sunan kişinin adıdır. Bu problem aslında matematiğin sezgilere aykırı halinin iyi bir örneğidir. Bu nedenle uzun zamandır gündemde varlığını sürdürmektedir. Bu problemin cevabı “21 Filminde” de kullanılmış sonrasında da sevgili seçiminizde neden değişiklik yapmanız gerektiğinin bir nedeni olarak bile savunulmaya başlanmıştır. ( Bu kısmı merak ederseniz kaynaklara göz atabilirsiniz)
Let’s Make A Deal Yarışmasının Kuralları Nedir?
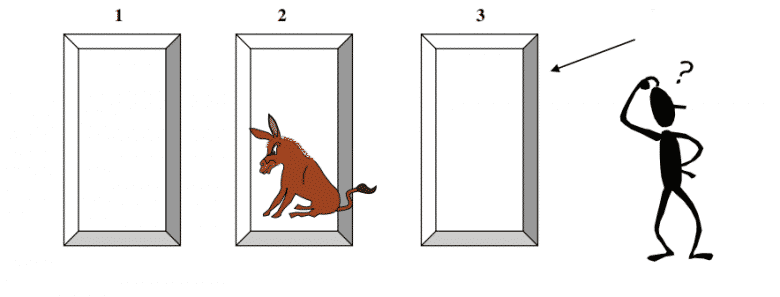
Birçok kişi zaten bu yarışmaya aşinadır ancak yine de TV hiç seyretmeyenler olabileceğini düşünerek kısaca kuralları anlatalım. Yarışma programında yarışmacılara üç kapalı kapı gösterilir. Bunlardan birinin arkasında araba gibi değeri yüksek bir ödül yer alır. Diğer ikisinin arkasında da keçi gibi düşük değerli bir ödül bulunur.
Yarışmacılar doğru kapıyı açar ise ödülü kazanır. Aksi takdirde ise hiçbir şey kazanamazlar. Daha sonra yarışmacılardan bir kapı seçmeleri ve hangi kapıyı seçtiklerini söylemeleri istenir. Yarışmacı seçim yaptıktan sonra ise geriye kalan iki kapıdan biri açılır.
Şimdi elinizde seçtiğiniz kapı ve seçilmemiş diğer kapı ile kaldınız. Bunlardan birinde büyük ödül olduğu kesin. Ve teklif gelir: “Kararınızı değiştirmek ister misiniz?” Yarışmacı kutusunu değiştirmeli mi, değiştirmemeli mi? Burada kazanma olasılığı en yüksek olan strateji nedir? Bu soruya yaygın biçimde verilen ve genel kabul gibi gözüken cevap ise evettir.
Birazdan nedenini açıklayacağımız gibi bu tür bir seçim sayesinde kazanma olasılığınızı iki katına çıkarmanız mümkündür. Ancak ne yazık ki kabul gören bu cevap her zaman bize doğru sonucu vermeyecektir. Kapıları değiştirip değiştirmemeniz tamamen sunucunun ne bildiği ya da bilmediği ile alakalıdır. Bunun nedenine geçmeden önce problemin genel olarak kabul görülen cevabının nasıl bulunduğuna bakalım.
Monty Hall Problemi Çözümü
İlk önce, sunucunun arabanın hangi kapının arkasında olduğunu bildiğini varsayalım. Yarışmacı olarak siz, bir kapı seçtiğinizde sunucu elbette arkasında keçi olan kapılardan birini açacaktır. Bu son derece mantıklı. Aksi halde yarışma sona erer ve tüm kurgu ortadan kalkar.
Şimdi diyelim ki siz üç numaralı kapıyı seçtiniz ve sunucu iki numaralı kapıyı açtı. Kapınıza bağlı kalmaya karar verirseniz ve ilk tahmininiz doğruysa kazanırsınız. Bunun olasılığı 1/3’tür ve sunucunun arkasında keçi olan kapıyı açması bunu değiştirmez. Kapıları değiştirirseniz ve ilk tahmininiz yanlışsa yine kazanırsınız. Bunun olasılığı 2/3 olur.
Monty Hall Problemi Değişime Kucak Açmamızı Önerir
Sayılar üzerinden giderek baktığınız zaman kazanma olasılığınız iki katına çıkmış gibi gözükür. Bu akıl yürütme, Monty Hall sorunun kabul gören cevabıdır. Olaya bu problem bazında baktığınız zaman da doğrudur. Değiştirmek iyidir çünkü bu sayede kazanma olasılığınız daha yüksektir. Ancak bu olasılık sunucunun bir keçi göstermesi ile ilgili değildir. Sonucunuz hala başlangıçta seçmediğiniz ve ev sahibinin açmadığı üçüncü kapıya bağlıdır.
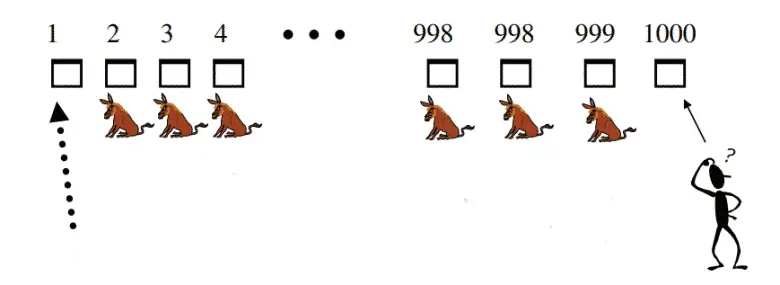
Ama ya sunucu arabanın nerede olduğunu bilmiyorsa? Bunun sonucunda da siz kapınızı seçtikten sonra rastgele bir kapı açarsa? Bu durumda açılan kapının bir keçiyi ortaya çıkarması, seçtiğiniz kapı hakkında size yeni bilgiler verir. Bir kapı elendiğinden, seçtiğiniz kapının arabanın olduğu kapı olma olasılığı artık daha yüksektir.
Kapınızın arkasında bir araba olma ihtimali artık 1/2 olacaktır. Bu durumda kapıyı değiştirseniz de değiştirmeseniz de kazanma olasılığınızda herhangi bir fark bulunmayacaktır. Bu nedenle, Monty Hall problemini hatırlatan bir durumla karşılaştığınızda, yapılacak en iyi şeyin değişimi kucaklamak olduğunu düşünmeyin. Her şey, kimin neyi bildiğine dair temel varsayımlara bağlıdır.
Bir B olayının meydana geldiğine göre , bir A olayının meydana gelme olasılığını nasıl hesaplayacağınızı söyleyen Bayes teoremini kullanarak yukarıdaki mantığı daha açık hale getirebiliriz. Örneğimizde, seçtiğiniz kapının arkasında araba olması olayını A, sunucunun arkasında keçi olan kapıyı açma olayını da B olarak kabul edelim.
Bu durumda P(A) yani arkasında araba olan kapıyı seçme olasılığınız 1/3’tür. Sunucu arabanın nerede olduğunu biliyorsa, her zaman arkasından bir keçi olan kapıyı açacaktır. Bu nedenle de P(B)=1 olacaktır.
Monty Hall Problemini Bayes Teoremi İle İnceleyelim
Şimdi bunları aşağıda gördüğünüz Bayes teoremi formülünde yerlerine yazalım. Formülde P(B|A) ifadesinin ne olduğunu merak edebilirsiniz. Bu ifade siz arkasında araba olan kapıyı seçtiğiniz zaman sunucunun arkasında keçi bulunan bir kapıyı açma olasılığıdır. Sonuçta sunucu her zaman arkasında bir keçi bulunan kapı açacağına göre aslında bizim seçimimizden bağımsız olarak P(B|A)=1 olacaktır.
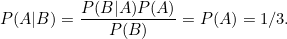
Bu nedenle, arabanın sizin seçmediğiniz kapının arkasında olması ve sunucunun açmamış olma olasılığı 1-1/3=2/3 kadardır. Ancak, sunucu arabanın nerede olduğunu bilmiyor ve rastgele bir kapı açıyorsa, bu durumda işler değişir. Artık, P(B) yani sunucunun arkasında bir keçi olan kapıyı açma olasılığı 2/3’e eşittir.
Ayrıca, sunucu sizinle aynı kapıyı seçmeyeceğinden, P(B|A) olasılığı (sizin arkasında araba olan kapıyı seçtiğinizde, sunucunun arkasında bir keçi olan kapı seçmesi) olasılığı da 1’e eşittir. Şimdi tüm bu bilgileri bir kez daha Bayes teoreminde yerlerine yazalım. Sonucun artık aynı olmadığını görebilirsiniz.
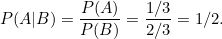
Sonuçta herhangi bir değişim fikrini kucaklamadan ve seçimlerimizi değiştirmeden önce değişimin kimden geldiğini ve aslında bu kişinin sonucu bilip bilmediğini sorgulamak iyi bir fikirdir. Ayrıca göz atmak isterseniz: Matematikçileri Ve Filozofları Onlarca Yıldır Oyalayan Uyuyan Güzel Problemi Nedir?
Kaynaklar ve ileri okumalar:
- Dr. Alfred S. Posamentier; Mathematics entertainment for the millions; ISBN 9789811219283; 2020 – World Scientific Publishing
- A Point of View: Why embracing change is the key to happiness; Yayınlanma tarihi: 8 Ekim 2013; Bağlantı: https://www.bbc.com/news/magazine-23986212
- Myths of maths: The Monty Hall problem; yayınlanma tarihi: 23 mart 2020; Bağlantı: https://plus.maths.org/
- Here’s the easiest way to understand the Monty Hall problem, the mathematics puzzle about goats that even PhD-holders get wrong; Yayınlanma tarihi: 3 Aralık 2016; Bağlantı: https://www.businessinsider.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel