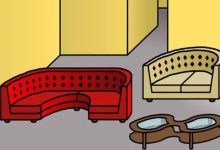
Size biri diğerinden iki kat daha fazla para içeren iki zarf verildiğini hayal edin. Bir zarfı seçmeniz gerekiyor. Siz zarfınızı seçtikten sonra daha siz zarfınıza bakmadan karşınızdaki kişi size bir teklifte bulunuyor. İsterseniz elinizdeki zarfı diğer zarf ile değiştirebilirsiniz. Seçtiğiniz zarfa bağlı mı kalmalısınız yoksa değiştirmelisiniz? Okuduğunuz bu soru değişim paradoksu ya da iki zarf problemi / paradoksu ( Two envelopes problem) adı ile bilinir.

Değişim paradoksu olarak da bilinen iki zarf paradoksu, olasılık teorisinde pek çok yanlış anlaşılmaya yol açan, iyi bilinen bir sorundur. İlk olarak 1912 yılında önde gelen Alman sayı teorisyeni Edmund Landau tarafından geliştirilmiştir.
Normalde herhangi bir fark olmayacakmış gibi gözükse de matematik size her zaman değiştirmeniz gerektiğini söylemektedir. Bu durum da sezgilere aykırı biçimde olduğu için bir paradoks olarak isimlendirilir. Neden değiştirmeniz gerektiğini anlamak için öncelikle beklenen değer hesaplaması hakkında bilgi sahibi olmanız gerekmektedir.
Beklenen Değer Nedir?
Olasılık teorisinde beklenen değer, bir şeyin olası sonuçlarının olasılığını yansıtan bir ortalamadır. Hilesiz bir zar attığınız zaman 1’den 6’ya kadar her sayının gelme olasılığı aynıdır. Bu, zarları birçok kez atarsanız, tüm atışların yaklaşık 1/6’sında 1’i; 1/6’sında 2’yi, 1/6’sında 3’ü görmeniz gerektiği anlamına gelir.
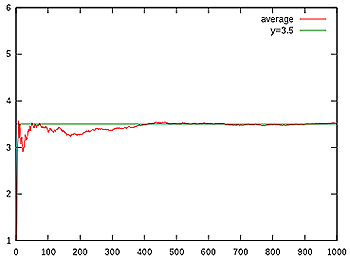
Yani zarı n kez atarsanız, her bir sonuç kabaca n/6 kez gerçekleşir. Güçlü büyük sayılar yasası, sayı büyüdükçe gerçek ortalamanın 3.5’e yaklaştığını söyler. 3.5 sayısı, bir anlamda, zarı sonsuz sayıda atmış olsaydınız elde edeceğiniz ortalamadır. Bunu aşağıdaki hesaplama ile elde edebiliriz.
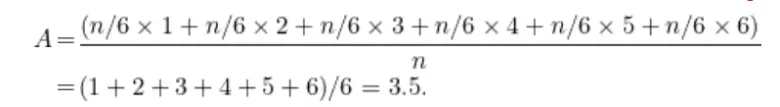
Aynı fikir daha genel olarak şu biçimde olur. 1 gelme olasılığının p1, 2 gelme olasılığının p2 olduğunu ve bu şekilde devam ettiğini varsayalım. Çok sayıda zar atışının ortalama sonucu bu durumda kabaca aşağıdaki gibi olacaktır.
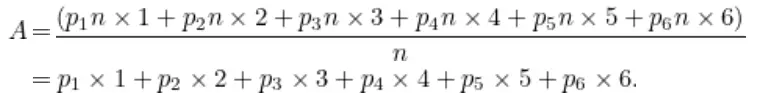
Bu durumda artık beklenen değer tanımını yapabiliriz. Rastgele bir değişkenin X1 ila Xm arasında m olası sonucu varsa ve karşılık gelen olasılıklar p1 ila pm ise, sonucun beklenen değeri aşağıdaki formül ile hesaplanır.
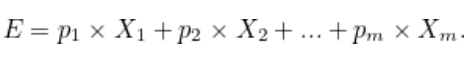
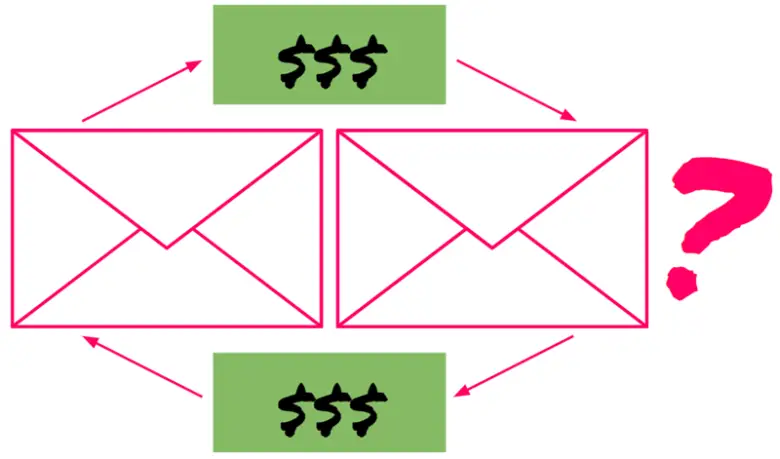
Şimdi iki zarf problemimize geri dönebiliriz. Diyelim ki seçtiğiniz zarftaki miktar x kadar. Bu durumda diğer zarftaki para miktarı 2x ya da x/2 kadar olmalıdır. Sonuçta her ikisinin de olasılığı 1/2 kadardır. Şimdi yukardaki formül yardımı ile beklenen değeri hesaplarsak sonuç aşağıdaki gibi olacaktır.
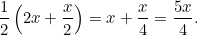
Gördüğünüz gibi bu sonuç başlangıçtaki x değerinden daha fazladır. Bu nedenle zarfı değiştirmeniz önerilir. Ancak zarfı değiştirdikten sonra size bir kere daha aynı teklif yapılırsa bir kere daha zarfı değiştirmelisiniz. Bir sonrakinde de aynı şeyi yapmalısınız. Bu durumda daha fazla para kazanmak adına hiç para kazanamayacaksınız gibi gözüküyor. Peki sorun nerede?
İki Zarf Problemi Çözümünü Nasıl Düşünmeliyiz?
Gördüğünüz gibi her zaman diğer zarfın beklenen değeri seçilen zarfınkinden daha büyük olacaktır. Bu durumda her zaman elimizdeki zarfı değiştirmeliyiz. Elbette burada bir mantık hatası olduğu aşikar. Bunun temel nedeni birbirine bağımlı olaylara bağımsız gibi davranmamız ile ilgilidir. Aslında bu paradoks ile ilgili bir çok çözüm vardır. Bunlardan bir tanesi toplam para miktarı üzerinden düşünmektir.
Zarflardan birinin x, diğerinin ise 2x kadar para barındırdığını kabul edersek toplam para 3x olacaktır. Bu durumda, eğer bir birey bir zarf seçer ve ona geçiş yapma seçeneği verilirse, birey geçiş yaptığında x miktarda para kazanabilir veya aynı geçişten sonra x miktarda para kaybedebilir. Her ikisinin de olma olasılığı ½’dir. Sonuç olarak, beklenen değer şimdi (-x).1/2+ (x).1/2= 0 biçimindedir. Gördüğünüz gibi bu durumda değiştirmek anlamsızdır. Ortada bir paradoks yoktur.
Problem İçin İkinci Çözüm
Daha önce bahsedildiği gibi, zarfı değiştirmek büyük ölçüde kişinin yaptığı ilk tercihe bağlıdır. Sonuç olarak, bu paradoks koşullu olasılık kullanılarak da çözülebilir. Seçilen ilk zarfın adı ‘A’ ve diğerinin adı ‘B’ olsun. Herhangi bir zarftaki küçük değer “x” ve diğer zarftaki değer ise “2x” olsun.
Önce ‘A’ seçildiği için, ‘B’nin beklenen değeri = 1/2 (A>B olduğu zaman B’nin beklenen değeri) + 1/2 (B>A olduğu zaman B’nin beklenen değeri) = 1/2 (x+2x) = 3x/2 olacaktır. Önce A seçmemiz durumunda da aynı hesaplamayı yapmamız gerekmektedir. Sonuç olarak, her iki zarfın da aynı beklenen değere sahip olması nedeniyle değiştirmenin anlamsız olduğu açıktır.
Bulduğumuz sonuç aslında ortada bir paradoks olmadığını anlamamız açısından yeterlidir. Ancak şu anda bir çok matematikçinin bu probleme alternatif bir çözüm bulmaya çalıştığını bilmek de sizi şaşırtacaktır. Problemin farklı varyasyonlarını ele alan birçok makale yayınlanmış, bu makalelerin her birinde ardında yatan matematiğe yönelik farklı açıklamalar sunulmuştur. Ancak yine de konu hakkında henüz bir fikir birliğine varılmamıştır.
Kaynaklar ve ileri okumalar
- Two envelopes problem; Bağlantı: https://en.wikipedia.org
- Maths in a minute: The two envelopes problem. Yayınlanma tarihi: 26 Eylül 2017; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel