Sigma Yunan alfabesinin 18. harfidir ve s harfi anlamına gelir. Büyük harf sigma (∑ ) matematikte toplamı ifade etmek için kullanılmaktadır. Küçük sigma harfi ise (σ) istatistikte standart sapmanın simgesidir. Peki ama 5 ya da 6 sigma nedir?

Söz konusu olan şey bilim ise asla kesin ifadeler ile konuşamazsanız. Bilimde bir sonucun kesin ya da anlamlı olması istatistiksel olarak da anlamlı olmasına bağlıdır. İstatistiksel anlamlılıktan bahsettiğimiz zamanlarda, tercih edilen ölçü birimi standart sapmadır.
Standart Sapma Nedir?
Bilim insanlarının çalışmalarında standart sapmayı nasıl kullandıklarını anlamak için tanıdık bir istatistiksel aracı yani bir madeni parayı kullanalım. Sonucunda bir madeni paranın bir yüzü tura, diğer yüzü de yazıdır. Bir atıştan sonra herhangi bir yüzün gelme olasılığı yüzde 50’dir. Bu durumda 100 kez yazı tura atarsanız, 50 tura ve 50 yazı gelme ihtimaliniz vardır. Ancak elbette 100 defa yazı tura atmayı denerseniz elde edeceğiniz sonuç 45-55 ya da 20-80 gibi de olabilir.
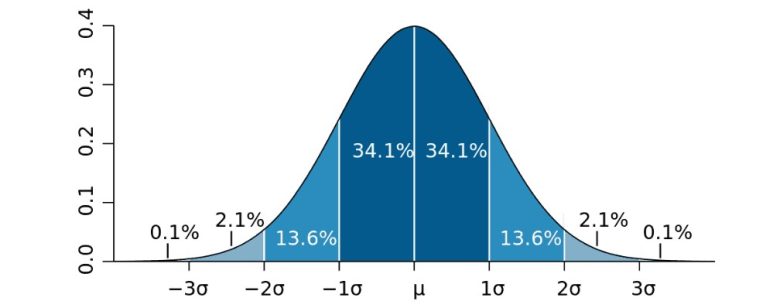
Tüm bu yazı tura test sonuçlarını bir grafik üzerinde çizerseniz, genellikle çan şeklinde bir eğri görürsünüz. Normal dağılım dediğimiz şey budur. Bozuk para örneğimizi ele alırsak normalimiz yani ortalamamız 50 dir.
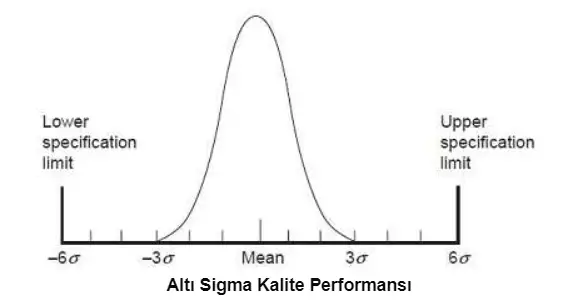
Yukardaki grafiği dikkatle incelerseniz x ekseni üzerinde bazı değerlerin olduğunu ve sigma sembolü ile gösterildiğini fark edeceksiniz. Ortalama değerin üstünde veya altında bir standart sapma veya bir sigma, tüm veri noktalarının yüzde 68’ini içerir. İki sigma yüzde 95’i ve üç sigma yüzde 99.7’yi içerir. Daha yüksek sigma değerleri, keşfin şans eseri olma olasılığının giderek azaldığı anlamına gelir.
Standart Sapma Nasıl Hesaplanır?
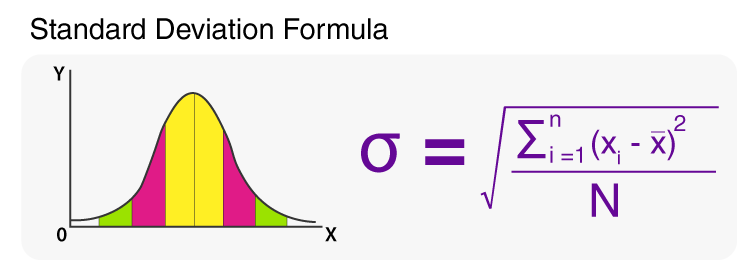
Bir sayı listesiyle karşılaştığımızda, bu sayıların ne kadar büyük veya küçük olduğu hakkında kabaca bir fikir edinmek için genellikle ortalamasına bakarız. Ancak ortalama bize bir çok şey hakkında yeterince fikir vermez.
Örnek olarak, beş arkadaşınıza yıllık maaşlarını sorduğunuzu ve cevapları aldığınızı düşünün. Bu maaşlar 20000, 20000, 20000, 20000 ve 100000 olsun. Bu maaşların ortalamasını alırsanız yani hepsini toplayıp 5 ile bölerseniz 36000 sonucunu elde ederseniz. Ancak bu sayı fazla anlamlı değildir. Sonuçta grubun çoğunluğunun maaşını temsil etmemektedir.
Bu durumda varyansa bakmanız gereklidir. Varyansı hesaplarken öncelikle her maaşı ortalamadan çıkartıp, sonucun karesini almalıyız. Kare almamızın nedeni negatif bir sonuç elde etme ihtimalini ortadan kaldırmaktır. Bu durumda yukarıdaki örneğimizin varyansı aşağıdaki gibi olacaktır.
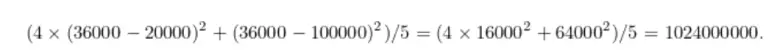
Bu çok büyük bir sayıdır. Bu da bize beş sayımızın hepsinin ortalamadan oldukça uzakta olduğunu gösterir. Yani diğer bir değişle veri setimiz çok dağınıktır. Eğer son arkadaşımız 100.000 yerine 20001 lira kazanmış olsaydı, varyans hesabının sonucunda 0,16 elde ederdik. Bu küçük bir sayıdır ve bu sayı kümesinin fazla dağılmadığını gösterir.
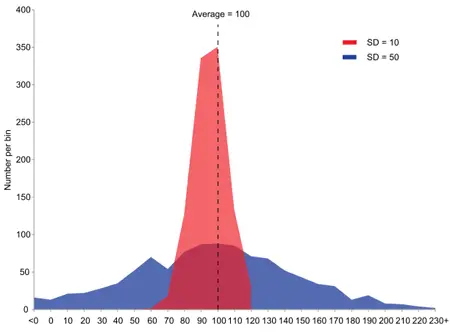
Bir popülasyonun varyansı, rastgele işlemi çok sayıda tekrarlarsanız sonuçların ne kadar yayılmış olabileceği konusunda size bir fikir verir. Varyansın pozitif kareköküne standart sapma denir. Standart sapmayı anladığımıza göre “6 sigma nedir?” sorusunun cevabına geçebiliriz.
İstatistikte 6 Sigma Nedir?
Altı sigma, sonucun rastgele bir tesadüf sonucu olmasının yarım milyarda bir olması anlamına gelir. Diğer bir deyişle bir sürecin mükemmellikten ne kadar saptığının istatistiksel bir ölçüsünü ifade eder. Altı sigma’da işleyen bir sürecin başarısızlık oranı yalnızca %0,00034’tür, bu da neredeyse hiç kusur olmadığı anlamına gelecektir.
| Sigma Seviyesi | Milyonda Olası Hata Adedi | Yüzde |
| 1 Sigma | 697700 | 30,23 |
| 2 Sigma | 308700 | 69,13 |
| 3 Sigma | 66810 | 93,32 |
| 4 Sigma | 6210 | 99,3790 |
| 5 Sigma | 233 | 99,97670 |
| 6 Sigma | 3,4 | 99,999660 |
Her ne kadar kökeni istatistik olsa da günümüzde 6 sigma terimi kendisine çalışma yaşantımızda bir yer bulmuştur. Altı Sigma yöntemini uygulayan şirketler, süreçlerinin verimliliğini sigma seviyesi adı verilen bir endeksle izlemektedirler.
İşletmelerde Uygulanan 6 Sigma Yöntemi Nedir?
Bir basketbol takımının sahibi olduğunuzu varsayalım. Doğal olarak takımınızın önümüzdeki sezon yapacağı maçları kazanmasını istiyorsunuz. Bunu iki şekilde başarabilirsiniz. Bu yollardan ilki, takımınızın muhteşem atışlar, smaçlar, top kesmeler ve asistler ile olağanüstü oyunlar çıkarmasıdır. Bu yolu seçmeniz halinde oyunun, bir iki yıldız oyuncu üzerine kurulması gerekecektir. Bununla birlikte maçları oyun esnasında daha az hata yaparak da kazanmanız mümkündür.
Benzer durum şirketler için de geçerlidir. Büyük buluşlar yaparak, çok önemli yenilikler gerçekleştirerek, başarılı isimleri şirkete transfer ederek yada diğer şirketleri satın alarak para kazanmak mümkündür. Öte yandan zaman ve kaynakları boşa harcamayarak veya hata oranı düşük ürün/hizmete odaklanarak da para kazanmak mümkündür. Bu da bizi Altı Sigma fikrine götürecektir.
Motorola kaliteyi zor yoldan – büyük zararlar, rekabetçi konumun kaybı, iflasın eşiğine gelme vb. – öğrenen pek çok şirketten sadece biridir. Ancak Motorola’nın bu öğrenme sonrası verimlilik, üretkenlik, karlılık, müşteri tatmini gibi konularda sağladığı olağanüstü başarılar onu diğerlerinden ayırmaktadır.
Şirketin 1988 yılındaki Genel Müdürü Bob Galvin’in, Beyaz Sarayda Malcolm Baldrige Kalite Ödülü’nü alırken, bu başarıyı Altı Sigma olarak adlandırdıkları bir yaklaşıma borçlu olduklarını söylemesi, Altı Sigma’yı çok sayıda şirketin ilgi odağı haline getirmiştir.
Altı rakamı ise hedeflenen kusursuzluk düzeyi ile ilgilidir. Örneğin bir sigma seviyesinde çalışan bir
işletme 1.000.000 işlemde yaklaşık 700.000 hata yapar. Eğer işletme iki sigmada çalışıyorsa, bu onun 1.000.000 işlemde ortalama 300.000 hata yaptığı anlamındadır. Şirketlerin büyük bir kısmı, üç ile dört sigma arasında faaliyet gösterir.
Sonuç Olarak;
Bazen 6-sigma bir sonuçtan ‘süper emin’ olmak için yeterli değildir. 2011’de CERN’den OPERA adlı bir deney, neredeyse kütlesiz nötrinoların ışıktan daha hızlı hareket ettiğini bulmuştu. 6 sigma güvenini taşıyan bu iddia, Einstein’ın görelilik ilkesini doğrudan ihlal ettiği için haklı olarak tartışmalıydı. Daha sonra, dört bağımsız deney aynı güven düzeyine ulaşamadı. Bu nedenle, bir sonucun kabul edilen anlamlılık aralığının içinde olması, onu mutlaka gerçekten önemli kılmayacaktır.
Yazının devamında bu yazımıza da göz atmak isteyebilirsiniz: Tip 1 ve Tip 2 Hata Nedir? Neden Dikkat Etmemiz Gerekir?
Kaynaklar ve ileri okumalar:
- Altı Sigma Nedir? ISSN:1306-3111, e-Journal of New World Sciences Academy 2008, Volume: 4, Number. 1, Article Number: E0002; https://dergipark.org.tr/
- What does 5-sigma mean in science?. yayınlanma tarihi: 6 Ocak 2021; Bağlantı: https://www.zmescience.com/
- Explained: Sigma. Bağlantı: https://news.mit.edu/
- Kadry, Seifedine. (2013). Six Sigma Methodology for the Environment Sustainable Development. 10.1007/978-94-007-5995-4_4.
Matematiksel










