Normalde bir cismi döndürmek veya ötelemek, hatta parçalamak o cismin toplam hacmini değiştirmez. Bunlar bizim geometriyle ilgili temel sezgilerimizdir. Ancak sonsuz çikolata ve Banach-Tarski Paradoksu bu sezgilerimize meydan okur.

Ormanda yürüyüş yapan iki arkadaş hayal edin. Acıkırlar ve bir elmayı bölmeye karar verirler, ancak yarım elma yetersiz gelir. Sonra içlerinden biri hayatında karşılaştığı en garip fikirlerden birini hatırlar. Bu, en azından prensipte bir elmayı iki elmaya dönüştürmeyi mümkün kılan, sonsuzlukla ilgili bir matematiksel bir teoremdir.
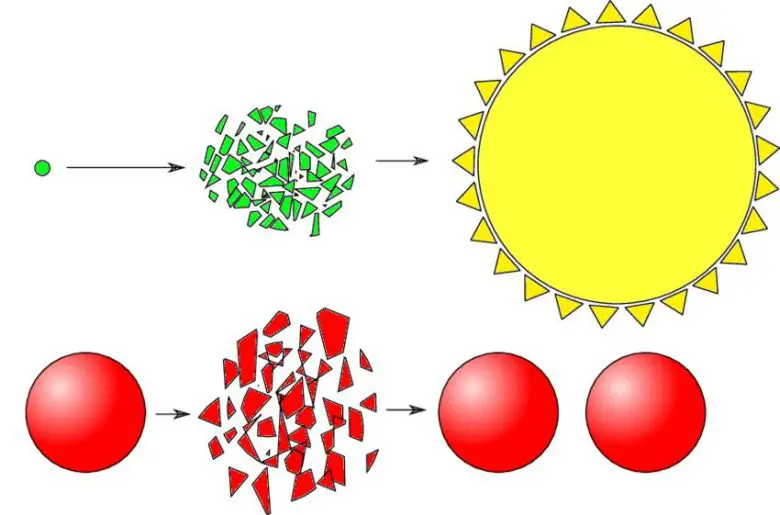
Bu argümana, 1924’te bunu ortaya atan matematikçiler Stefan Banach ve Alfred Tarski’nin anısına Banach-Tarski paradoksu denir. Matematiğin temel kurallarına göre, üç boyutlu katı bir topu parçalara ayırmanın ve bu parçaların birleşerek orijinalinin iki özdeş kopyasını oluşturmasının mümkün olduğunu kanıtlar.

Bu bir elmadan iki elma yapmak anlamına da gelecektir. Hiçbir şeyden bir şey elde etmeninin mümkün olduğunu gösterir. Diğer bir deyişle de 1+1=1 olacaktır. Banach-Tarski Paradoksuna geçmeden önce bu paradoksun daha eğlenceli bir versiyonuna göz atalım.
Hiç Bitmeyen Çikolata: Sonsuz Çikolata
Çikolatayı hepimiz severiz ancak muhtemel bir çikolata ile ilgili sevmediğimiz şey onun bitmesidir. Ancak son zamanlarda internette karşımıza çıkan bir çikolata numarası bunun aslında mümkün olduğunu bizlere gösteriyor.

5 × 5 dikdörtgen parçalardan oluşan bir çikolatayı aşağıdaki şekildeki gibi kesip sonrasında yeniden birleştirirseniz elinizde her zaman fazladan bir çikolata parçası kalacaktır. Sonsuz çikolata paradoksu, Banach-Tarski paradoksunun kabaca bir temsili gibidir. ( Ancak aynı şey değildir)
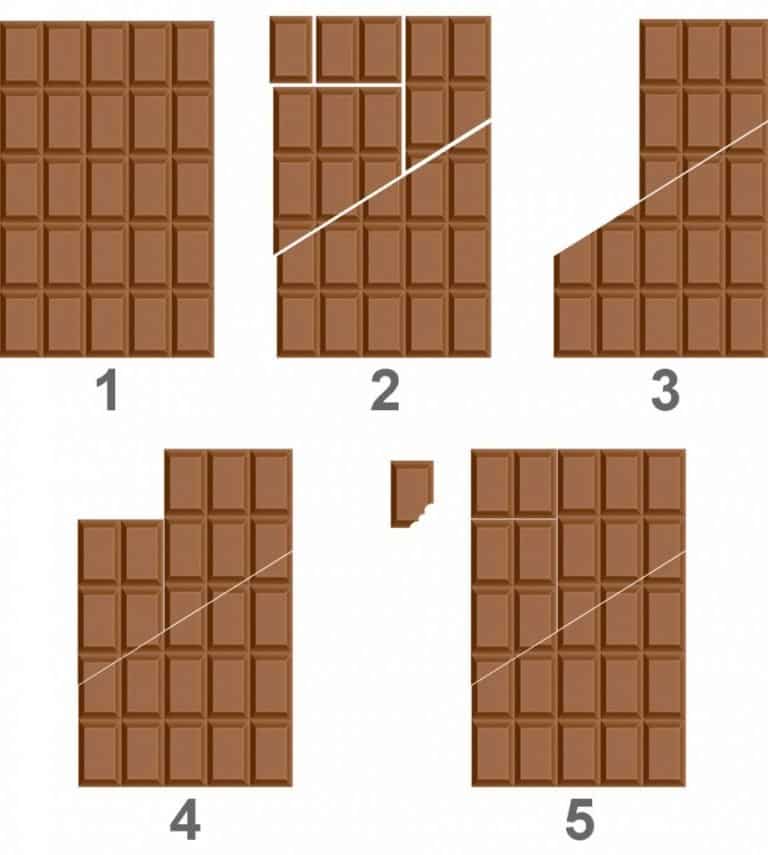
Paradoksu gösteren gif büyük ölçüde yanılsama içermektedir. Çünkü parçalar yeniden düzenlendiğinde ortaya çıkan çikolata, başlangıçtaki çikolata ile aynı ölçüde değildir. Evde denemek isterseniz öncesinde ve sonrasında dikey uzunlukları ölçtüğümüz zaman çikolatanın boyunun kısaldığını siz de görebilirsiniz. Şimdi asıl konumuza dönebiliriz.
Banach-Tarski paradoksu nedir?
Polonyalı bir matematikçi olan Stefan Banach (1892-1945) 20. yüzyılın en önemli matematikçilerinden ve bilim insanlarından biriydi. Kendisi matematiğin vektör uzaylarıyla ve bu uzayların üzerinde tanımlı işlemlerle uğraşan bir alt dalı olan fonksiyonel analizin kurucularındandı.
1924’da Banach, başka bir matematikçi Alfred Tarski ile çalıştı. Sonunda ikili bir küreyi altıya bölüp parçaların yerlerinin değiştirdiğinizde ilk baştaki küreyle aynı boyutlara sahip iki farklı küreyi nasıl elde edebileceğinizi gösterdiler.

Çalışmaları, Öklid uzayının belirli alt kümeleri için benzer bir paradoksal ayrıştırmayı gösteren Avusturyalı matematikçi Felix Hausdorff’un daha önceki keşiflerine dayanıyordu. Banach ve Tarski, 3 boyutlu küre için şaşırtıcı sonuçlarını kanıtlamak için Hausdorff’un çalışmalarını genişlettiler. Burada “paradoks” kelimesi, fizik yasalarıyla çelişiyor gibi göründüğü için kullanılır, ancak kanıt hiçbir mantıksal çelişki içermez
Seçim Aksiyomu Nedir?
Banach-Tarski paradoksunu mümkün kılan matematiksel kurala seçim aksiyomu denir. Bu aksiyom genellikle kümelerden eleman seçmeyi gerektiren durumlarda karşımıza çıkar. Modern matematiğin temeli olarak hizmet eden Zermelo-Fraenkel küme teorisindeki dokuz aksiyomdan biridir.
Seçimlerimizin geçerli olması için tutarlı olması gerekir. Elimizde bilye dolu üç tane kutu varsa ve bir kutudan bir bilye seçersek ve sonra zamanda geriye gidip tekrar seçersek, seçtiğimiz ilk bilyenin orada olacağını biliriz. Ancak birbirinden ayırt edilemeyen bilyeler içeren sonsuz sayıda kutu varsa sorun yaşarız. Bu tip senaryolarda seçim aksiyomu her zaman aynı bilyeyi seçecek biçimde çalışır. Yani ilk seçimlerin nasıl yapıldığını hesaba katmamıza gerek olmaz bu da çoğu zaman paradoksal sonuçlara ulaşmamıza neden olur.
Seçim aksiyomunun paradoksal sonuçlarından dolayı bu aksiyomu matematikte kabul etmek istemeyenler olmuştur. Ancak matematikçilerin büyük çoğunluğu aksiyomun matematik için gerekli olduğunu düşünmektedir. Çünkü istatistik ve fizik için çok önemli olan bazı çalışma alanları seçim aksiyomu üzerine kurulmuştur.
Banach-Tarski paradoksu sonsuzluğun doğası ile ilgilidir.
Sonsuzluk bir sayı gibi hissedilir, ancak öyle davranmaz. Sonsuzluğa herhangi bir sonlu sayıyı ekleyebilir veya çıkarabilirsiniz ve sonuç yine de başladığınız sonsuzlukla aynıdır. Ancak bu, tüm sonsuzlukların eşit olduğu anlamına gelmez.
Geçtiğimiz yüzyılda, matematikçiler bazılarının diğerlerinden daha büyük olduğunu kanıtladılar. Örneğin, doğal sayılar (1, 2, 3, vb.) sayılabilir bir sonsuzluktur. Sonsuza kadar devam ederler, ancak onları saymak mümkündür (1’den 1 trilyona kadar olan sayıları listelemek gibi).
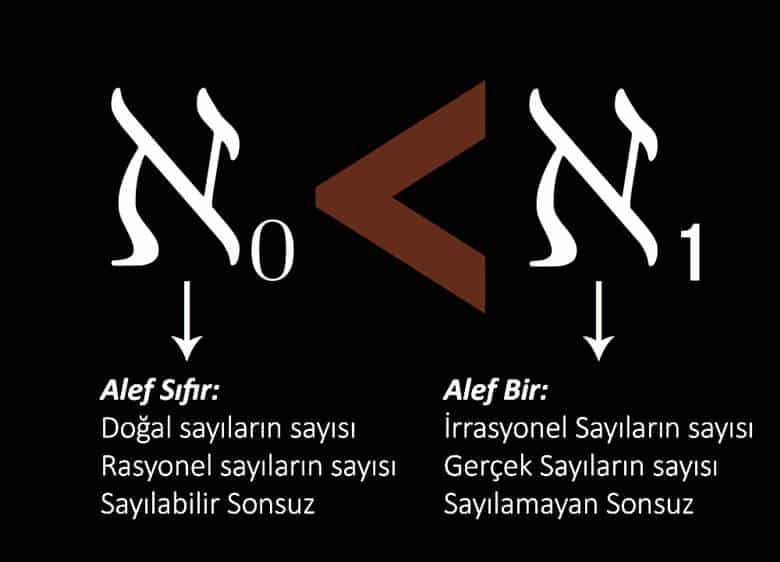
Buna karşılık, gerçek sayılar sayılamaz bir sonsuzluktur. Sıfır ile 1 arasında görünüşte çok küçük olan aralıklarda olsalar bile, gerçek sayıları sayamazsınız. Sayılabilir ve sayılamaz sonsuzluk arasındaki bu fark, doğal sayıları gerçek sayılardan daha küçük bir sonsuzluk yapar. Bu nedenle matematikçiler ikisinin farklı “kardinaliteye” sahip olduğunu söyler.
1891’de Georg Cantor, bir doğru üzerindeki sonsuz sayıdaki noktanın, küre gibi bir şeklin hacmini dolduran sonsuz sayıdaki noktayla aynı kardinaliteye sahip olduğunu kanıtlamıştı. Banach ve Tarski, sayılamayacak kadar sonsuz sayıda noktayı bölümlere ayırarak bir küreyi ikiye dönüştürebileceğinizi fark etti. Ve hatta yeni kürenin de aynı biçimde parçalanması mümkündü. Üstelik bu işlemi sonsuza kadar devam ettirebilirdiniz.
Banach-Tarski paradoksu neden ortaya çıkıyor?
Bunun için kürede herhangi bir nokta ve iki açı seçin (açınız, irrasyonel olmalıdır). Bu açılardan birini Kuzey-Güney dönüşleri için diğeri ise Doğu-Batı dönüşleri için kullanacaksınız. Şimdi küreyi seçtiğiniz açı kadar döndürün. Bu döndürme hareketi sonucunda yukarı, aşağı, sağ ya da solda yeni bir nokta elde ettiniz. ( Doğu’ya döndükten hemen sonra Batı’ya dönmeyin.) Bu süreci sonsuz sayıda tekrarlarsanız, sonsuz sayıda nokta elde edersiniz.
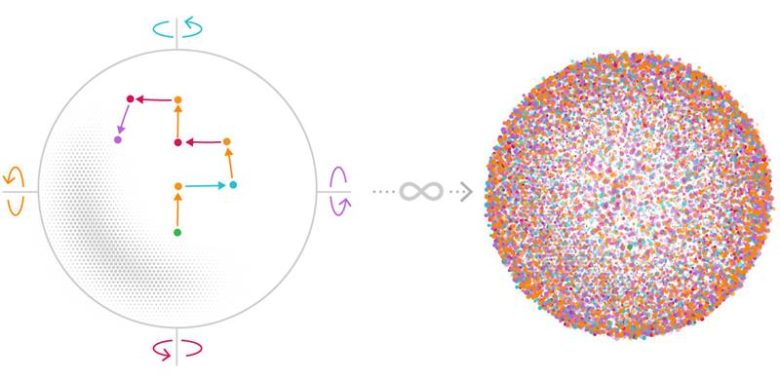
Bu kümenin birkaç temel özelliği vardır. Birincisi, aynı noktayı birden fazla içermez. Ayrıca küme sayılabilir sonsuzlukta olacaktır çünkü her noktaya doğal bir sayı atamanız mümkündür. Şimdi bu kümemizdeki noktaları son hamlede döndüğümüz yere göre gruplandıralım. Artık elimizde kuzey, güney, doğu ya da batıya dönme sonucu elde ettiğimiz gruplarımız artı merkez ile kutuplardaki noktalarımız ve başlangıç noktalarımız vardır. (Her dizinin iki dönme kutbu vardır ve bunlar tam olarak başladıkları yere geri dönen noktalardır. )
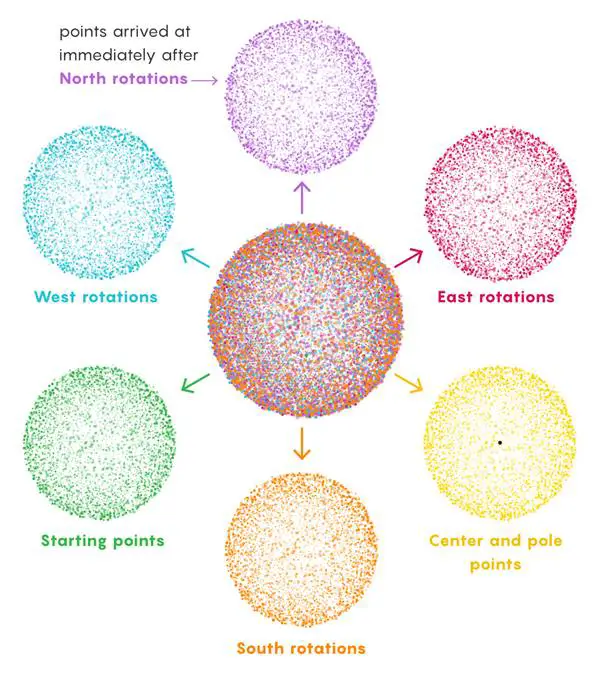
Şimdi Doğu’ya doğru son bir döndürmeden elde edilen tüm noktaları Batı’ya çevirin. Bu, tüm son Doğu yönündeki döndürmeleri geçersiz kılar. Grubu, hemen önce gelen (hala sonsuz) noktalar koleksiyonuna dönüştürür. Artık ikinci sırada gelenler başa geçmiştir ve bunlar kuzey, güney ve doğu ile başlamak zorundadır. ( Batı yoktur çünkü iki ters yönün yanyana olmasına izin verilmiyordu.)
Sonrasında da kuzey grubunu güneye döndürün, bu size tüm kuzey, doğu ve batı noktalarını verecektir. Son olarak, kutupları ve merkez noktasını kopyalamamız gerekir. Bu, David Hilbert’in adı ile anılan sonsuzlukla ilgili argümana benzer bir süreçle gerçekleşir.
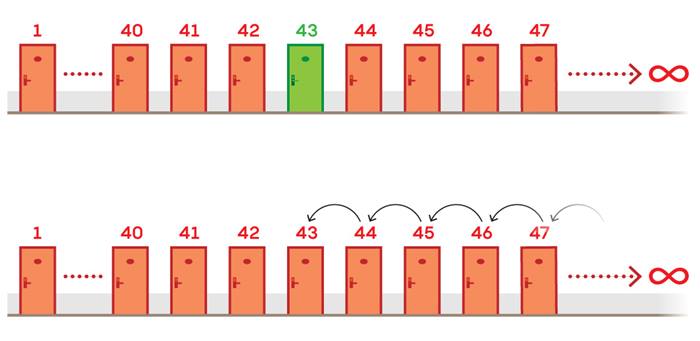
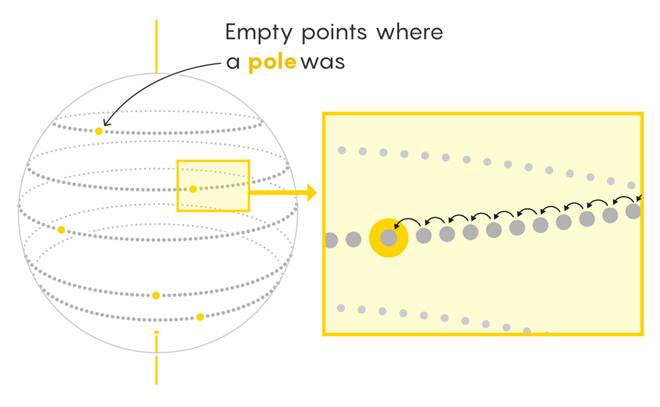
Bu düşünce deneyinde, sonsuz sayıda odası olan bir otel hayal edin. Sadece 43 numaralı odanın boş olduğunu varsayalım. 44 numaralı ve üzeri odalardaki tüm misafirleri alın ve bir oda aşağı taşıyın. Boşluğu yeni bir oda yaratmadan doldurmuş olursunuz. Elimizdeki yeni kürede kutup noktaları boş kalmıştı. görseldeki gibi her enlem çizgisindeki tüm noktaları kaydırın. Sonsuzluk boşlukları dolduracaktır. Boş merkez noktası da için de aynı şey geçerli olacaktır. Artık ikinci küremizi yapmaya hazırız.
Sonuç olarak
Bu teorem sağduyuya meydan okur. Ancak yine de sonuç doğrudur. Elbette ki Banach-Tarski sonsuz karmaşıklıkta şekillerdir, basit fiziksel dünyada realize edilebilecek şeyler değillerdir. Dolayısıyla platin bir küreyi Banach-Tarski parçalarına ayırıp, daha sonra bu parçaları birleştirerek iki yeni küre elde edeceğiniz ve bir vagon dolusu değerli metal elde edene kadar bu işleme devam edeceğiniz işletme modeli işe yaramayacaktır. Ancak Banach-Tarski paradoksu matematikteki en ilginç sonuçlardan birini yansıtmaktadır.
Kaynaklar ve ileri okumalar:
- What Is The Infinite Chocolate Paradox?; Yayınlanma tarihi: 1 Mart 2022. Kaynak site. Science ABC. Bağlantı: What Is The Infinite Chocolate Paradox
- Wahlberg, Mats. (2022). The Banach-Tarski Paradox. 10.48550/arXiv.2206.13512.
- Banach-Tarski and the Paradox of Infinite Cloning; Yayınlanma tarihi: 25 Ağustos 2021. Kaynak site: Quanta Magazine. Bağlantı: Banach-Tarski and the Paradox of Infinite Cloning
Matematiksel










