
On dokuzuncu yüzyılın sonunda, Rus ressam Nikolai Petrovich Belsky (1868–1945), 1895 yılında “Mental Arithmetic. In the People’s School of SA Rachinsky” isimli bu tablosunu tamamladı. Resim, 19. yüzyılın sonlarına ait bir köy okulunu ve bu okuldaki bir aritmetik dersini tasvir ediyordu. Resimdeki öğretmen ise Sergei Alexandrovich Rachinsky (1833-1902) idi.
Moskova Üniversitesi’nde profesör olan matematikçi Rachinsky, 1872’de üniversitedeki görevinden istifa edip köyüne dönmüştü. Buradaki köy okulunda devrim niteliğinde çalışmalar yapmış ve matematik öğretmek için benzersiz yöntemler geliştirmişti.
Raçinski’nin on yıl süren köy öğretmenliği zamanında yetişen gençler Moskova ve Petersburg Üniversitelerinde “Tatevolular” unvanıyla şöhret kazanırlar. Tatevolular arasından birçok mühendis, makineci ve doktor çıkar. Kendisi de Rachinsky’nin eski bir öğrencisi olan Belsky, çalışmalarına, bu okula ait anılarını sıklıkla yansıtmıştı.

Çocukluğunda yaşadığı bir anıdan mıdır yoksa tamamen kurgusal mıdır bilinmese de resimde tahtada yazılan bir soru üzerine düşünen ve kafalarından hesap yapmaya çalışan öğrencileri görüyoruz. Yüz ifadelerine bakıldığı zaman bu öğrencilerin soru karşısında zorlandıklarını görmek mümkün. Aslında resme daha dikkatli bakıldığı zaman tahtada gerçek bir matematik sorusu yazıldığı görülüyor. Tahtadaki soru aşağıdaki gibi.
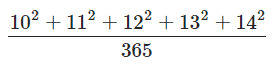
Hesap makinesi olmadan bu sorunu çözmeye çalıştığınızı hayal edin. Kesinlikle yapılabilirsiniz ancak bu biraz zaman alıcıdır. Bununla birlikte, sayılar arasında var olan harika ilişkiler sayesinde, sorunun cevabını çok kısa sürede yapmanız mümkündür. Hatta bu ilişkiyi tam olarak anladıktan sonra sizde başka rakamlar ile başka sorular oluşturabilir ve etrafınızda aynı şaşkınlığı yaratabilirsiniz.
Resimdeki Soruyu Nasıl Çözebiliriz?
Bu soruyu çözmenin yolu pay kısmında bulunan sayıları gruplayarak düşünmektir. Öncelikle 10,11 ve 12 sayılarının kareleri toplamına bir göz atalım. 102+112+122=365 yapacaktır. Şimdi de 13 ve 14 için hesaba bakalım. 132+142 nin de 365 yaptığını göreceksiniz. Bu durumda ilginç bir ilişki keşfetmiş olduk. 102+112+122=132+142
Bu sayede sorunun cevabı da 730/365 bölmesini sonucunda iki olarak bulunacaktır. Aslında bu bir kuraldan ziyade cebirsel ifadelerin matematiksel işlemleri yapmada nasıl kullanılabileceğini gösteren keyifli bir örnektir. Tahtadaki soruyu aşağıdaki gibi düşünürsek, birçok sayı parantezler açıldığında birbirini götürdüğü için çözümü sağlayan tek sayının 12 olduğunu kolayca görebiliriz.
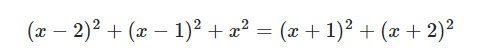
Bu Matematik Sorusu Üzerine Nasıl Bir Genelleme yapabiliriz?
Şimdi tahtada gördüğümüz rakamları yukarıdaki eşitlikte yerlerine yazalım. Bu durumda işlemimiz 102+112+122+132+142 = (12 – 2)2+(12 – 1)2+122+(12 +1)2+(12 + 2)2 biçiminde olacaktır. Gerekli açılımları yaptığımız zaman 5 x122+2 x 4 + 2 x 1 elde ederiz. Şimdi öğrendiğimiz bu bilgiyi 482 + 492 + 502 + 512 + 522 sonucunu hesaplamak için kullanalım. Yukarıdaki mantığı buraya uygularsanız cevap 5. 502+ 2.4+2.1 olacaktır. 12510 cevabını da bu aşamadan sonra birçok kişi aklından verebilecektir.
Aynı biçimde 842 + 87 2 + 90 2 + 932 + 962 işleminin cevabının da 5 x 902+2 x 36+2 x 9 oluğunu ve sonucun fazlada zorlanmadan 40590 çıktığını da söyleyebiliriz. Bu kalıbı anlayanlar aslında aşağıdaki örnekte de benzer kalıp olduğunu fark edeceklerdir. 212 + 222 + 232 + 242 = 252 + 262 + 272 = 2030
Yukarıdaki mantıkla bu hesabı da cebirsel ifadeler biçiminde yazabilir ve bulduğunuz sonuçları kolaylıkla başka sayılara uygulayabilirsiniz Bu tür hesaplamaları bir hesap makinesi ile yapmak mümkün olsa da, hesaplamamızı kolaylaştırmak için bir model aramak daha eğlenceli olabilir. Gördüğünüz gibi resim aslında oldukça akıllıca düşünülmüş bir matematik sorusu içermektedir. Bu da idealist öğretmen Raçinski’nin dehasının bir işaretidir. Yazının devamında göz atmak isterseniz: Çarpma Yapmanın Eğlenceli İki Yolu: Rus Çiftçi Ve Antik Mısır Çarpımı
Kaynaklar ve ileri okumalar:
- Alfred S. Posamentier; Mathematical Curiosities: A Treasure Trove of Unexpected Entertainments; 2014; Prometheus Books
- How do people perform mental arithmetic for complicated expressions?; Bağlantı: https://math.stackexchange.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






