Nehir kıyısında yapılan basit bir yürüyüş, matematiğin tamamen yeni bir dalının doğmasına ilham verebilir mi? Bu yürüyüşü yapan kişi Leonhard Euler ise aklınıza evet cevabı gelmelidir. Königsberg Köprüsü ile ilgili bir bilmece matematiği gerçekten de pek çok açıdan değiştirmiştir.

Baltık Denizi kıyısında Litvanya ve Polonya arasında sıkışmış Rusya’nın Kaliningrad Oblastı olarak bilinen bir bölgesi var. Burası II. Dünya Savaşı’ndan sonrasında aceleyle inşa edilen kalitesiz gri apartmanlarla dolu kasvetli bir sanayi şehridir. Bu sadece mimarlığı sevenler için değil, aynı zamanda nostaljik matematikçiler için de üzücüdür.
Çünkü tüm zamanların en büyük matematikçilerinden biri olan Leonhard Euler, 18. yüzyılda burada bulunan Königsberg şehrinin düzeni sayesinde, sonunda matematiğin iki yeni alanına, topoloji ve çizge teorisine, katkıda bulunan bir bulmacayı yanıtlamıştı.
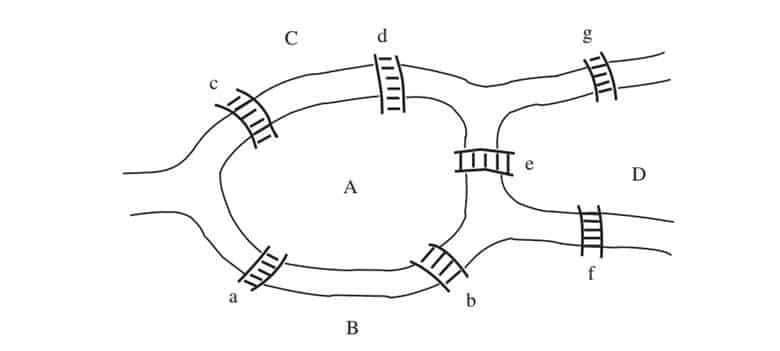
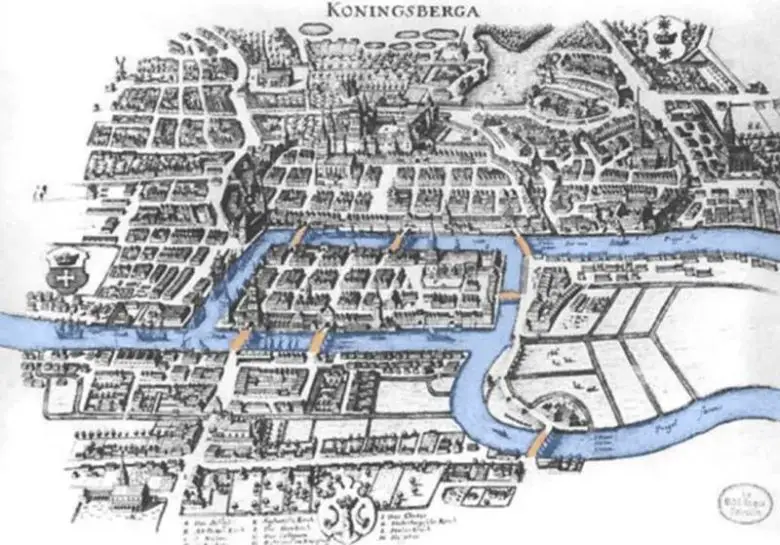
Königsberg, Pregel nehrinin kıyısında inşa edilmiştir. Yedi köprü, iki adayı ve nehrin kıyılarını birbirine bağlıyordu. Königsberg vatandaşlarının çoğu Pazar öğleden sonralarını şehirde dolaşarak geçiriyordu. Sonra zamanla bir eğlence başladı. Dolaşmaya çıkanlar her köprüyü yalnızca bir kez geçerek şehrin içinde yürüyebilir mi?
Königsbergliler farklı yollardan yürümeyi denediler ama kimse her köprüyü tam olarak bir kez geçip başlangıç noktasına dönmenin yolunu bulamadı. Bu soru zamanla, Königsberg Köprüsü problemi, Königsberg’in yedi köprüsü problemi olarak bilindi. Bulmaca o kadar meşhur oldu ki İsviçreli matematikçi Leonhard Euler’in kulağına kadar ulaştı ve o da bu bulmacayı çözmeye karar verdi.
Euler’in Königsberg İle İlgisi Ne?
Carl Leonhard Euler o zamanlarda, Königsberg’in yaklaşık 130 km. batısında bulunan Prusya’da bir şehir olan Danzig’in belediye başkanıydı. 1736’da Euler’e yazılan bir mektup, Königsberg Köprüsü probleminden haberdar olmasını sağladı. Euler’in ise bu probleme bir cevap vermesi sadece 4 gününü alacaktı.
Bulmacayı çözmenin bir yolu, şehir içinde çok sayıda farklı rota denemektir. Ancak bu yol çok uzun zaman alacaktı. Euler, konuyla ilgisiz bilgileri görmezden gelerek bulmacayı çözmenin daha kolay olacağını düşündü. Örneğin Königsberg haritasının problemle hiçbir ilgisi yoktu, önemli olan sadece köprülerdi.
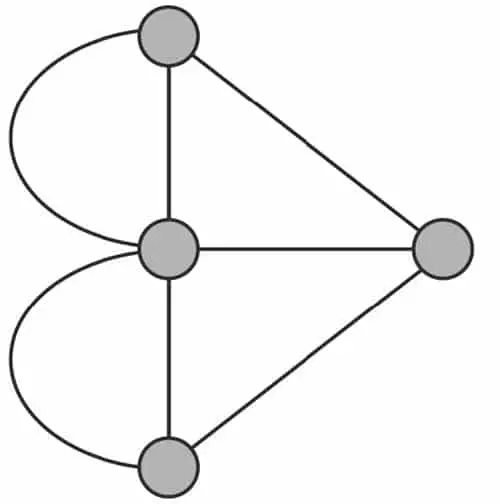
Böylece köprüleri çizgi, adaları ve anakarayı da daire şeklinde çizdi. Bir köprüden diğerine ancak ikisi de aynı daireye bağlıysa yürümek mümkün olabilirdi. Euler’in Königsberg bulmacası ile ilgili yukarıda gördüğünüz çizimi, günümüzde çizge (graf) olarak bilinen şeyin ilk örneğidir.
Matematikte graf ya da çizge, düğümler ve bu düğümleri birbirine bağlayan kenarlardan oluşan bir tür ağ yapısıdır. Sosyal ağlar, ulaşım ağları veya internet gibi ağlarla çevrili olduğumuz için graf teorisi modern matematikte önemli bir rol oynar.
Königsberg Köprüsü Problemi Çözümü Nedir?
Probleminin çözümünü, 1735’te Euler Petersburg Akademisi üyelerine sundu. Çözümü basitçe şu şekilde aktarabiliriz. Euler öncelikle her bir daireyi ( düğümü) ‘tek’ veya ‘çift’ olarak tanımladı. Bir düğüm, kendisinden çıkan tek sayıda çizgi varsa tektir aksi halde çifttir. Sonunda da kuralını belirledi.
Her yolun sadece bir kez kullanıldığı bir devre, devrede hiç tek dereceli düğüm yoksa ya da iki tane tek dereceli düğüm varsa mümkündür. Ayrıca eğer iki tek düğüm varsa, devreden geçen yol tek düğümlerden birinde başlamalı ve diğerinde bitmelidir.
Böyle bir yürüyüşü gerçekleştirmek isteyen kişinin iki seçeneği vardır. Seçeneklerinden ilki bir tur yapmaktır yani başladığı noktada yürüyüşünün bitirmektir. Diğer seçenek ise bir noktada yürüyüşe başlayıp başka bir yerde yürüyüşü tamamlamaktır. Önemli olan tek bir şey vardır. O da her köprüyü sadece bir kez geçmek.
Aynı köprüden gidip geri dönmek bu nedenle mümkün değildir. Eğer ilk senaryodaki gibi bir yürüyüş yapar yani bir tur atarsanız yola çıktığınız kara parçasına bağlı en az iki köprü olması gerekir. Birini giderken diğerini de dönerken kullanacaksınız. Yani köprü sayısı çift olmalıdır. Grafik üzerinde düşünürsek de her daireye çift sayıda çizgi bağlı olmalıdır.
Farklı bir başlangıç ve bitiş noktası olan ikinci senaryodaki gibi bir yürüyüşte, başlangıç noktasında bir köprü ve bitiş noktasında bir köprü vardır. Yürüyüşünüz esnasında da bir köprüden kara parçasına ayak basar, diğer köprüden de çıkarak yolunuza devam ederseniz.
Bu durumda eğer A noktasından B noktasına gidiyorsanız yola A noktasındaki köprüden geçerek çıkmalı sonra bir giriş bir çıkış iki ucu olan bir kara parçasından geçmeli ve son olarak bir köprü ile B noktasında varmalısınız. Şimdi yukarıdaki grafiğe göz atın. Her ada parçasına bağlı tek sayıda çizgi olduğunu göreceksiniz. İşte bu nedenle Königsberg şehrinin içinde her köprüden bir kere geçerek dolaşmak imkansızdır.
Ya 8. Köprü Eklenirse?
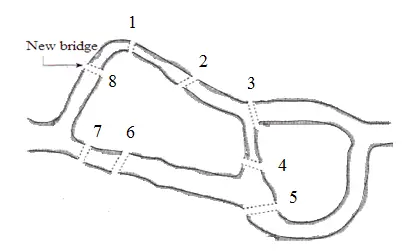
19. yüzyılın sonlarında bölgeye 8. köprü inşa edildi. Bu da elbette bulmacanın cevabını değiştirdi. Çünkü bu sayede artık başlanılan noktaya geri dönmeden turu tamamlamak mümkün olmuştu. Çünkü tek düğümlerin sayısı ikiye düşmüştü ve tura başlayan herkes bu tek düğümlerin birinden yola çıkıp diğerinde turunu tamamlıyordu.
Ne yazık ki, 1944’te hava saldırıları eski köprülerin çoğunu yok etti. Ancak Königsbergerliler farkında olmadan Euler devrelerinin keşfedilmesini sağlamışlardı. Günümüzde bu devreler ile uğraşanların eğlenceden farklı amaçları olduğunu muhtemel tahmin edebilirsiniz. Bu fikir artık Google Haritalar ile rotaları planlamak için de kullanılıyor. Königsberg Köprüsü probleminin ilginç bir uygulamasını bu yazımızda da okuyabilirsiniz: Üç Ev Üç Kuyu Problemini Neden Yıllardır Çözemiyoruz?
Kaynaklar ve ileri okumalar:
- Why Do Buses Come in Threes?: The Hidden Maths of Everyday Life; Jeremy Wyndham;ISBN-10 : 9780471379072
- The bridges of Königsberg. yayınlanma tarihi: 5 Ağustos 2016; Bağlantı: The bridges of Königsberg
- How the Königsberg bridge problem changed mathematics – Dan Van der Vieren. Kaynak site: Ted Ed: Bağlantı: How the Königsberg bridge problem changed mathematics – Dan Van der Vieren
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









