Kaos Teorisi doğal olarak öngörülemeyen sistemlerin davranışlarını tahmin etme bilimidir. İnsan kalbinin atışı ve asteroitlerin yörüngeleri gibi çok çeşitli doğal sistemlerin karmaşık işleyişine açılan bir penceredir. Kaotik bir dünyayı anlamamıza yarayan matematiksel bir araçtır. Hava durumu veya yeni yürümeye başlayan bir çocuğun davranışı gibi belirli sistemlerin temelde öngörülemez olmasıyla bağlantılıdır. Modern matematiğin en muhteşem alanlarından birine hoş geldiniz.

19. yüzyılda Fransız matematikçi Pierre Laplace, 1814 tarihli bir denemesinde şöyle demişti. Evrendeki tüm parçacıkların konumlarını ve hızlarını kesin olarak bilseydik, geleceği kesin olarak tahmin edebilirdik. Yani kendisi bir gün, hava tahminlerden gezegenlerin yörüngelerine kadar her şeyi kusursuz biçimde tahmin edeceğimizi ön görmüştü.
Isaac Newton ise fiziği, saat gibi işleyen bir evreni yöneten bir dizi kural olarak düşünmüştü. Ancak kaos teorisi, en katı kuralların ve neredeyse mükemmel bilgilerin bile öngörülemeyen sonuçlara yol açabileceğini kanıtlar. Sonucunda kaotik bir dünyada, ne bekleyeceğinizi asla bilemezsiniz. Bir çok olay rastgele bir biçimde gerçekleşir. Ancak kaos ile rastgele aynı şey değildir.
Kaos rastgele ile tahmin edilebilir arasında bir yerdedir. Kaos teorisinin merkezinde, düzen ve kaosun her zaman taban tabana zıt olmadığı yönündeki büyüleyici fikir vardır. Kaotik sistemler bu ikisinin bir karışımıdır. Üstelik 1960’larda ve 70’lerde yapılan bir dizi keşif, kaos yaratmanın ne kadar kolay olduğunu göstermiştir.
Kaos Teorisi Nedir?
Kaos teorisi, hava durumu gibi başlangıç koşullarına son derece duyarlı dinamik sistemlerin davranışını açıklar. Bir ay, hatta bir yıl sonrasına ait hava tahminlerini bilmek gerçekten güzel olurdu. Ancak hava durumunu tahmin etmek hiçbir zaman tamamen çözemeyeceğimiz bazı zorlu sorunları da beraberinde getirir.
Bunun nedeni arka plandaki süreçlerin karmaşık olması değildir. Aslında çok daha temel bir şeydir. Bu pek çok açıdan öngörülemez ve kaotik bir evrende yaşadığımız gerçeğidir. Tüm kaotik sistemler, temelde basit olma yani matematiksel denklemlerle tanımlanma özelliği gösterir. Ancak bu denklemlerdeki en küçük değişiklikler öngörülemez ve tekrarlanamaz sonuçlara neden olur.
Fiziğin güzel yanlarından biri deterministik olmasıdır. Yani bir sistemin tüm özelliklerini biliyorsanız ve fizik yasalarını biliyorsanız, o zaman geleceği mükemmel bir şekilde tahmin etmek mümkündür. Ancak doğanın hem deterministik hem de öngörülemez olabileceği ortaya çıktı. Bunun ipuçlarını ilk kez 1800’lerde İsveç kralı üç cisim problemini çözebilecek herkese bir ödül teklif ettiğinde almıştık.
Fransız matematikçi Henri Poincaré problemi çözmeden ödülü kazanmıştı. Ancak kendisi sorunu çözmek yerine, sorunun çözülememesinin nedenlerini açıklayacaktı. Vurguladığı en önemli nedenlerden biri de sistemin başlangıcındaki küçük farklılıkların sonunda büyük farklılıklara yol açacağıydı. Bu kaotik evren fikrinin başlangıcıydı. Ancak kaos teorisi, Edward Lorenz’in 1963 yılındaki gözlemlerine kadar kimsenin ilgisini çekmeyecekti.
Kaos Teorisi İle Nasıl Tanıştık?
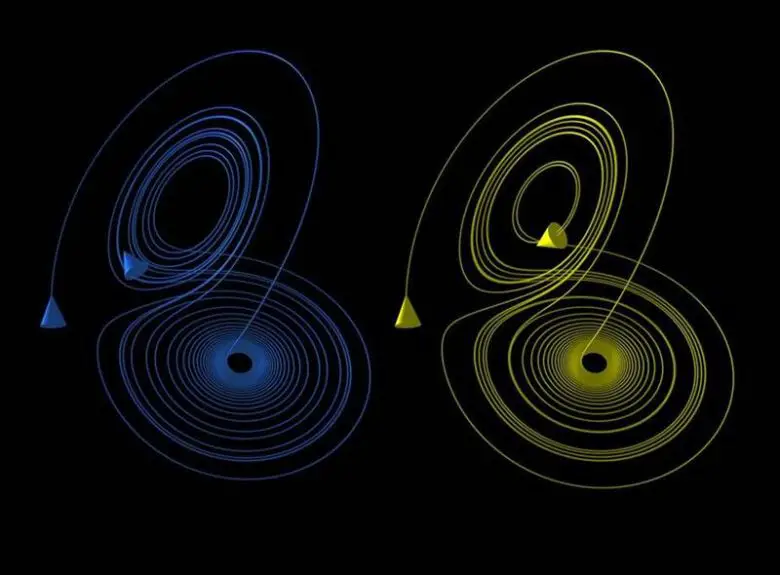
1960’ların başlarında, MIT meteoroloji profesörü Edward Lorenz, silah testlerinin planlanmasında ve uyduların yörüngeye fırlatılmasında kullanılan ana bilgisayarların doğru hava tahminleri vermeye yardımcı olacağına ikna olmuştu. Lorenz basit bir denklem seti oluşturdu ve denklemleri son model bir bilgisayara girdi. Kaos genelde insanların hiç beklemediği anda ortaya çıkar. Aslında sonrasında onun da başına gelen buydu.

bir süre aynı davranışı sürdürecek, ancak zamanla kaos, bunların birbirinden ayrılmasına neden olacaktır.
İlk veri setini girdi, bilgisayarı açtı ve çıktıyı bekledi. Çıktıyı makinenin yanına koyarak, bazı verileri yeniden girmeye ve programı daha uzun süre çalıştırmaya karar verdi. Ancak programın farklı bir tahmin vermişti. Sonunda, bilgisayar çıktısının verileri 0.506127 yerine 0.506 olarak yuvarladığını ve farkın bundan kaynaklandığını anlayacaktı.
Normalde, başlangıç koşullarındaki çok küçük değişikliklerle bir sistemi başlattığınızda, çıktıda yalnızca çok küçük değişiklikler elde edersiniz. Ancak hava durumu için durum böyle değildi. Küçük bir değişiklik (örneğin, Güney Amerika’da bir kelebeğin kanat çırpması), hava koşullarında çok büyük bir değişikliğe yol açmıştı. (Atlantik’te yeni bir kasırganın oluşması gibi). Lorenz aslında Poincaré ‘nin 63 yıl önceki bulgusunu ondan habersiz olarak yeniden bulmuştu. Kendisi Kelebek Etkisi ile karşı karşıya kalmıştı.

Bunun sonucunda anladık ki uzun dönemli hava tahminleri yapmak bir hayaldi. Küçük hatalar hep olacaktı. Kelebek Etkisi nedeniyle de bu küçücük hatalar bile zamanla büyüyüp bir hava tahminin büyük hatayla sonuçlanmasına sebep verecekti.
Lorenz Çekicisi Nedir?
Bu keşif inanılmaz sonuçlar doğurdu. Lorenz sadece kaosu keşfetmekle kalmadı, aynı zamanda onun anahtar mekanizmasını da belirledi. Bazı sistemler çekiciler adı verilen bir model sergiliyordu. Kaotik bir sistemin gizli yapısının kilidini açmanın anahtar çekicileri belirlemekti.

Bir pinpon topunu okyanusa attığınızı hayal edin. Suyun altından ya da üstünden nereden başlarsanız başlayın, top öngörülebilir bir şekilde çekicisine, yani okyanus yüzeyine doğru hareket edecektir. Sonrasında da bir kaos ortamında okyanusta batıp çıkarken, çekicisine tutunacaktır.
Kaotik bir sistemin an be an nasıl davranacağını tam olarak tahmin edemesek de, çekiciyi bilmek olasılıkları daraltmamıza olanak tanır. Ayrıca sistemin nasıl tepki vereceğini doğru bir şekilde tahmin etmemizi sağlar. Matematikçiler bir sistemin olası davranışlarını geometrik olarak tanımlamak için “faz uzayı” kavramını kullanırlar. Ancak bu faz uzayı normal uzay gibi değildir; faz uzayındaki her konum, sistemin farklı bir konfigürasyonuna karşılık gelir.
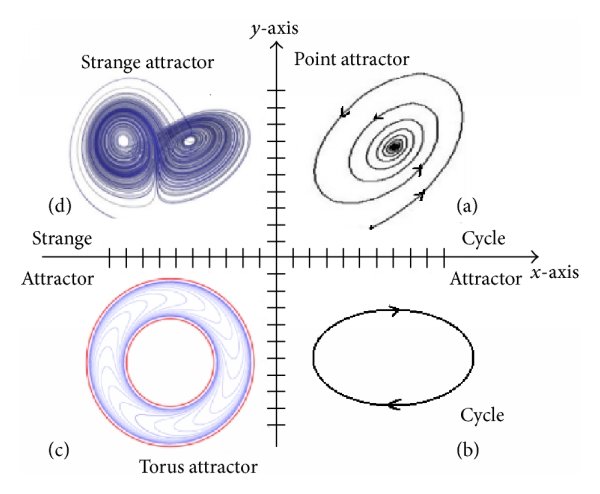
Kaotik bir sistem de faz uzayındaki çekicisine doğru hareket eder. Ancak noktalar veya basit döngüler yerine “tuhaf çekicilerin” ortaya çıktığını görüyoruz. Kendi içine bükülen ve karmaşık ayrıntılara sahip bu güzel şekiller kaos teorisini fraktal geometri ile bağlar. Matematikçi Benoît Mandelbröt’ün öncülüğünü yaptığı fraktal geometri, bu sistemin davranışını anlamamıza olanak tanır.

Kaos Teorisi İle Sadece Matematikçiler İlgilenmez
Kaos Teorisi yalnızca matematikçilerin ilgi alanına girmez. Sonucunda kaotik olaylar her yerdedir ve bu nedenle kaos teorisi; fizikçiler, biyologlar, bilgisayar bilimcileri ve ekonomistler gibi birçok farklı alandan uzmanları bir araya getirir.
Banyonuzda damlayan bir musluğu ve Büyük Hadron Çarpıştırıcısının soğutucu olarak kullandığı aşırı soğutulmuş sıvı helyumu düşünün. Her ikisi de ilk başta kaotik olmayan sistemlerdir, ancak helyumu yavaşça ısıttığınızda veya musluğu açtığınızda karakterleri değişecektir. Düzenden kaosa geçiş ise Feigenbaum sabiti adı verilen bir sayı tarafından kontrol edilmektedir.
Sonucunda damlayan musluklardan, gezegenlerin dansına kadar her yerde kaos vardır. Kaos Teorisi ise bize doğanın hayal ettiğimizden çok daha karmaşık ve şaşırtıcı olduğunu gösterir.
Kaynaklar ve ileri okumalar:
- Chaos Theory, The Butterfly Effect, And The Computer Glitch That Started It All. Yyaınlanma tarihi: 13 Şubat 2018. Kaynak site: Forbes. Bağlantı: Chaos Theory, The Butterfly Effect, And The Computer Glitch That Started It All
- Explainer: what is Chaos Theory? Yayınlanma tarihi: 19 Kasım 2012. Kaynak site: Conversation. Bağlantı: Explainer: what is Chaos Theory?
- What is chaos? A complex systems scientist explains. Yayınlanma tarihi: 7 Ekim 2012. Kaynak site: Conversation. Bağlantı: What is chaos? A complex systems scientist explains
- Oestreicher C. A history of chaos theory. Dialogues Clin Neurosci. 2007;9(3):279-89. doi: 10.31887/DCNS.2007.9.3/coestreicher. PMID: 17969865; PMCID: PMC3202497.
- Chaos theory explained: A deep dive into an unpredictable universe. Yaınlanma tarihi: 19 Kasım 2022. Kaynak site: Space. Bağlantı: Chaos theory explained: A deep dive into an unpredictable universe
- Adewumi, Aderemi & Kagamba, Jimmy & Alochukwu, Alex. (2016). Application of Chaos Theory in the Prediction of Motorised Traffic Flows on Urban Networks. Mathematical Problems in Engineering. 2016. 1-15. 10.1155/2016/5656734.
Matematiksel