Basit bir fikri asla küçümsemeyin çünkü bu fikirlerin bazen geniş kapsamlı etkileri olabilir. Böyle bir fikir için verilebilecek bir örnek, ilk olarak 1834’te Alman matematikçi Peter Gustav Lejeune Dirichlet (1805-1859) tarafından formüle edilen güvercin yuvası ilkesidir.

Güvercin yuvası ilkesinin tahmin ettiğiniz gibi güvercinler ile en ufak bir ilgisi yoktur. İlk olarak 1834’te formüle edilen bu ilke aslında başlangıçta çekmeceler ile ilgili idi. İşin içine güvercinler sonradan karıştı.
Sayı sayma fikri basit gelse de saymanın bilimsel olarak ele alınması nispeten yeni bir oluşumdur. Kriptografi, kodlama teorisi, kuyruk teorisi ve teorik bilgisayar bilimi, çeşitli sayma tekniklerini kullanır. Sayma teorisinin ilk ustalarından biri başta da dediğimiz gibi Peter Gustav Lejeune Dirichlet’ti.

Ve başlıca sayma tekniklerinden biri, orijinal olarak “Dirichletscher Schubfachschluss” (Dirichlet’in çekmece kapatma ilkesi) olarak adlandırılan tekniktir.
Güvercin Yuvası İlkesi Nedir?
Elinizde n tane nesne ve k tane çekmece olsun. Bu nesneleri çekmecelere yerleştirmek istediğiniz zaman çekmecelerden daha fazla nesne varsa ( n > k ), o zaman birkaç nesne aynı çekmecede birlikte bulunmak zorundadır. Matematiksel olarak ifade edersek eğer n nesne k kategori arasında bölünürse ve n > k ise o zaman en azından n ⁄ k nesne aynı kategoriye aittir.
Yani, nesneler çekmeceler arasında eşit olarak dağıtılırsa, ortalama olarak n ⁄ k nesne aynı çekmecede son bulur. ( Eğer n ⁄ k bölümü bir tamsayı değilse, aradığımız minimum değeri bir üst sayıya yuvarlamamız gerekir).
Bu durumda 5 tane kazağınız ve dört çekmeceli bir şifonyeriniz varsa, her çekmeceye bir kazak koyma şansınız yoktur. Benzer bir biçimde üç güvercin yuvanız ve dört güvercininiz olduğunu düşünelim. Tüm güvercinlerin bir güvercin yuvasına girmesi gerekiyor. Bu durumda elbette bir güvercin yuvasında birden fazla güvercin bulunmalıdır. Aşağıda gördüğünüz fonksiyon eşlemesi Güvercin yuvası ilkesinin özünü bizlere göstermektedir.
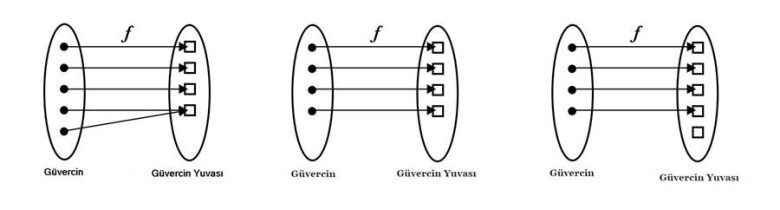
Mantığa tamamen uygun. Bunun matematik ile ne ilgisi var diye düşünüyorsanız aslında yanılıyorsunuz. Bir matematik teoreminden çok basit bir gözleme benzeyen bu ifade ilk kez 1622’de Fransız bilim insanı Jean Leurechon tarafından bir kitapta bahsedilmişti.

Ancak bir kere daha, hiçbir bilimsel buluşa gerçek kaşifinin adının verilmediğini söyleyen Stigler yasası geçerliliğini göstermişti. Bu nedenle Jean Leurechon’dan 200 yıl sonra yaşasa bile Güvercin yuvası ilkesi Peter Gustav Lejeune Dirichlet’e atfedilmektedir.
Güvercin Yuvası İlkesi İle Örnek
Güvercin yuvası ilkesi günlük hayatımızda bir çok ilginç biçimde karşımıza çıkar. Bu basit prensibi güvercin ve yuva özelinden çıkarıp çok geniş alanlara genişletebiliriz. Bu sayede de oldukça karmaşık ilişkileri kanıtlamayı mümkün kılar.
mutlaka bulunacaktır
Örneğin, 8,5 milyon kişinin yaşadığı bir şehirde en az 23.000 kişi aynı gün doğmuştur. Şehrin nüfusu yaklaşık 8,5 milyon ve birinin doğabileceği 366 farklı takvim günü (29 Şubat dahil) var. Buna göre en az 8.500.000 / 366 = 23.000 kişi aynı doğum gününe sahip sonucu ortaya çıkar.
En az altı öğrencinin aynı notları (A, B, C, D veya F olsun) alması için bir matematik sınıfında gereken minimum öğrenci sayısını bilmek istediğimizi varsayalım. Aslında bunu güvercin yuvası ilkesi ile hesaplamanız olasıdır. Diyelim ki n öğrenci sayısını temsil ediyor. ( yani güvercin). Ayrıca m ise notların sayısını gösteriyor ( yani yuva). Bu durumda n/5 işleminin sonucu 6 olmalıdır.
Burada minimum öğrenci sayısını bilmek istediğimizi anımsayalım. Bu nedenle cevabımız 30 değildir. Çünkü güvercin yuvası ilkesine göre n/5 işlemimizin sonucu tamsayı değil ise bir üstteki tamsayıya yuvarlanmalıdır. Bu durumda aradığımız cevap 26 olacaktır. ( 26/5=5,2). Yani bir sınıfta 26 öğrenci varsa en az 6 öğrenci aynı notları alacaktır.
Sonuç olarak
Güvercin yuvası ilkesi, görünüşte apaçık ifadelerin bile matematikte büyük bir değere sahip olduğunu gösterir. Ancak bu çok da şaşırtıcı olmamalı. Ne de olsa, matematiğin bir çok alanındaki çalışmalar, olabildiğince basit olan birkaç temel varsayıma dayanmaktadır. Sonucunda basit sistemlerin karmaşık sonuçları çıkacaktır.
Kaynaklar ve ileri okumalar:
- Dar, Zain. (2018). The Pigeonhole Principle and It’s Applications. 10.13140/RG.2.2.26177.45923.
- 16 fun applications of the pigeonhole principle; yayınlanma tarihi: 25 Kasım 2018. Bağlantı: 16 fun applications of the pigeonhole principle
- The Pigeonhole principle; Yayınlanma tarihi: 23 Ağustos 2019; Bağlantı: The Pigeonhole principle/
- Rittaud, B., Heeffer, A. The Pigeonhole Principle, Two Centuries Before Dirichlet. Math Intelligencer 36, 27–29 (2014). https://doi.org/10.1007/s00283-013-9389-1
- The World’s Simplest Theorem Shows That 8,000 People Globally. Have the Same Number of Hairs on Their Head. Yayınlanma tarihi: 20 mart 2023; bağlantı: The World’s Simplest Theorem Shows That 8,000 People Globally. Have the Same Number of Hairs on Their Head
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










