Örümcekler, doğada yalnızca dayanıklı ağlar örmekle kalmaz; aynı zamanda kusursuz bir matematiksel düzen kurarlar. İlk bakışta rastgeleymiş gibi görünen bu yapılar, gerçekte karmaşık bir geometri ve hassas hesaplamalar içerir.

Örümcek ipeği, yeryüzündeki en çok yönlü doğal malzemelerden biridir. Örümcekler bu olağanüstü ipliği yalnızca av yakalamak için değil; hareket ederken kendilerini güvenceye almak, barınak kurmak, eşlerine kur yapmak ve yumurtalarını korumak gibi birçok farklı amaçla kullanır. Her kullanım için ipeği farklı şekillerde üretir ve işlerler.
Bu kadar esnek ve işlevsel bir malzemeye sahip olmak, örümceklerin evrimsel süreçte çok çeşitli ağ yapıları geliştirmelerine olanak tanımıştır. Her tür, yaşadığı ortama ve avlandığı canlılara göre kendi özgün ağ mimarisini oluşturur.
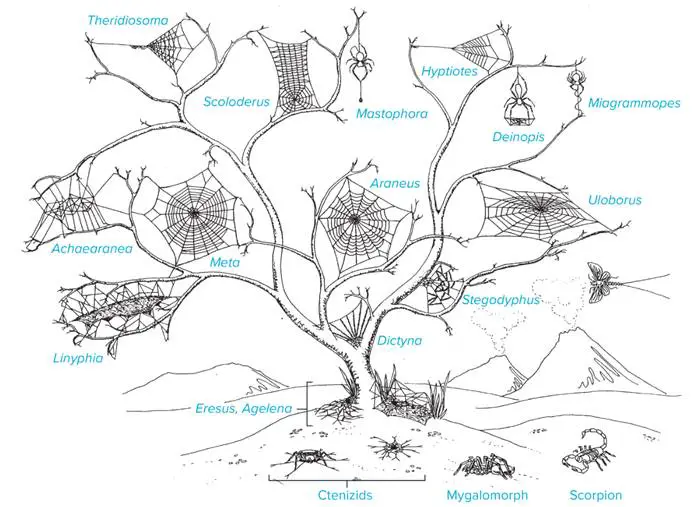
Örneğin dairesel örümcek ağlarını ele alalım. Bu iki boyutlu, havada asılı duran yapılar merkezden dışa doğru uzanan kollar ve onların etrafına örülmüş belirgin bir spiral içerir. Bu ağlar, özellikle sinek ve çekirge gibi uçan ya da sıçrayan avları yakalamak için tasarlanmıştır.
Buna karşılık, evlerin köşelerinde ve süpürgelik diplerinde sık rastladığımız ağlar farklı bir yapıdadır. Genellikle Theridiidae ailesine ait küçük, koyu renkli örümceklerin ördüğü bu ağlar, karmaşık ve üç boyutlu bir yapıya sahiptir. İlk bakışta dağınık görünseler de bu ağlar rastgele değil; belirli bir av yakalama stratejisine göre örülür.
Bu ağların alt kısmından yere doğru uzanan ipek hatlar, yüksek gerginlikle sabitlenmiştir. Bu hatlar, karınca ve böcek gibi yürüyerek dolaşan avlar için kurulmuş bir tuzaktır. Av, yere temas eden yapışkan noktaya bastığında ipek ani bir hareketle yerinden kopar ve bazen avı havaya kaldıracak kadar sert bir şekilde yukarı çeker. Böylece örümcek, ağın içinden çıkmadan önce avı etkisiz hâle getirmek için zaman kazanır.
Zıplayan Örümcekler: Sevimli Ama Ölümcül Avcılar
Zıplayan örümcekler, ağ ören en sıradışı türlerden biridir. Canlı renkleri, detaylı kur dansları ve şaşırtıcı derecede “sevimli” görünümleriyle tanınırlar. Hatta Joshua Slice tarafından yaratılan sevimli çizgi karakter Lucas the Spider sayesinde geniş bir hayran kitlesi bile kazanmışlardır.

Öne çıkan büyük gözleri sayesinde derinlik algısına sahip olan bu örümcekler, çevrelerini ustalıkla algılar ve her yöne zıplayarak hem gezinir hem de avlanırlar.
Peki ya bir zıplamayı yanlış hesaplarlarsa? Ya da bir yırtıcıdan kaçmaları gerekirse? İşte tam bu noktada ipek devreye girer. Zıplayan örümcekler, havaya atlamadan önce kendilerini bulundukları yüzeye bağlayan bir “emniyet ipi” bırakırlar. Eğer atlayış başarısız olursa, bu ipe tutunarak tekrar yukarı tırmanır ve yeniden deneme şansı bulurlar.
Ama bu ipek sadece bir güvenlik önlemi değildir. Aynı zamanda atlayışın kontrolünü sağlar. Zıplama sırasında ipeğin salınım hızını değiştirerek yönlerini ve iniş hızlarını ayarlarlar. Böylece tam istedikleri noktaya iniş yaparlar.

Bir Örümcek Ağını Nasıl Yapar?
Dairesel ağlardan ev içinde rastlanan karmaşık görünümlü ağlara kadar tüm örümcek ağları, belirli ve sistemli adımlarla inşa edilir. Bu ağlar yalnızca rastgele örülmüş iplik yığınları değildir; her biri, örümceğin yaşam tarzına ve avlanma stratejisine uygun şekilde şekillenir.
Örneğin, dairesel ağ ören örümcekler işe bir “ön ağ” oluşturarak başlar. Bu ilk aşama, bilim insanlarına göre örümceğin çevresini tanıdığı, alanı ölçtüğü ve ipeğini nereye sabitleyebileceğini belirlediği bir keşif sürecidir. Ön ağ hazırlandığında, örümcek bu yapıyı kullanarak ağın taşıyıcı çerçevesini, merkezden dışa doğru uzanan kollarını ve avı yakalayacak spiral yapısını inşa eder.
Bu karmaşık tasarımın önemli bir amacı vardır: Ağ, yalnızca küçük sinekleri değil, ortalama saatte 16 kilometre hızla uçabilen yusufçuk gibi güçlü avları da yakalayabilmelidir. Böyle bir böceğin ağdan geçip gitmesini önlemek için ağ hem dayanıklı hem de esnek olmak zorundadır. İnşa tamamlandığında örümcek, ağın merkezine yerleşir ve hareketsiz kalarak bir sonraki avını bekler.
Bu kadar işlevsel bir yapının tek bir tür ipekle oluşturulması mümkün değildir. Örümcekler, farklı görevler için özelleşmiş yedi farklı ipek türü üretir. Dairesel ağ ören türler, bu ipeklerin tamamını kullanır.
Örümcek, ağın çerçevesini ve taşıyıcı bölümlerini inşa ederken en sert ve dayanıklı ipek liflerini kullanır. Bu güçlü lifler, ağın genel yapısını taşır ve aynı zamanda örümceğin düşme ya da tehlike anında tutunabileceği bir emniyet ipi işlevi görür.
Buna karşılık, ağın ortasındaki av yakalama spirali çok daha esnek bir ipek türünden örülür. Bir böcek bu bölgeye çarptığında, oluşan darbe ipeği gerer. Esnek lifler bu enerjiyi emer ve yayar. Bu sayede ağ yırtılmaz, av da ağa saplanıp kalır.
Ayrıca sanılanın aksine örümcek ağı baştan sona yapışkan değildir. Yapışkanlık, yalnızca av yakalama spiralinde bulunan özel bir ipek türünden gelir. Bu ipek, örümceğin salgıladığı yapışkan maddeyle kaplıdır ve görevi, avı yeterince uzun süre ağda tutarak örümceğe yaklaşma ve zehirli ısırığını gerçekleştirme fırsatı sunmaktır.
Sonuç Olarak
Örümcekler ve ağları, doğanın sunduğu en yaratıcı ve işlevsel tasarımlardan bazılarını temsil eder. Her tür, kendi yaşam alanına ve av stratejisine göre farklı ağ yapıları geliştirerek çevresine kusursuz bir şekilde uyum sağlar. Bu nedenle bir örümcek ağıyla karşılaştığınızda, onu yok etmek yerine bir an durup incelemeyi deneyin.
Bu küçük ama usta mimarları izlemek, sadece doğaya değil; aynı zamanda mühendislik, mimarlık ve malzeme bilimine dair bakış açınızı da zenginleştirebilir. Çünkü çoğu zaman doğadaki en etkileyici çözümler, karmaşıklıktan değil, sadelikten doğar.
Kaynaklar ve ileri okumalar
- How spider silk is one of the most versatile materials on Earth. Yayınlanma tarihi: 12 Eylül 2019. Bağlantı: How spider silk is one of the most versatile materials on Earth./
- Sahni V, Harris J, Blackledge TA, Dhinojwala A. Cobweb-weaving spiders produce different attachment discs for locomotion and prey capture. Nat Commun. 2012;3:1106. doi: 10.1038/ncomms2099. PMID: 23033082.
- Vollrath, Fritz & Selden, Paul. (2007). The Role of Behavior in the Evolution of Spiders, Silks, and Webs. Annual Review of Ecology and Systematics. 38. 819-846. 10.1146/annurev.ecolsys.37.091305.110221.
- Corver, Abel & Wilkerson, Nicholas & Miller, Jeremiah & Gordus, Andrew. (2021). Distinct movement patterns generate stages of spider web building. Current Biology. 31. 10.1016/j.cub.2021.09.030.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





