İmkânsızın ustası M.C. Escher’in yanılsamalarla dolu dünyaları, sanatçıları, tasarımcıları, matematikçileri ve jeologları uzun süredir büyülemeye devam ediyor.

Escher, matematiksel bir yeteneği olmadığını söylese de, zamanla matematik ve bilim dünyasının önde gelen isimleriyle yakın ilişkiler kurdu. Bu isimler arasında Macar George Pólya, İngiliz Roger Penrose, Kanadalı Harold Coxeter ve Alman kristalograf Friedrich Haag gibi önemli bilim insanları yer alıyordu.
Çalışmaları 1950’lerin başına kadar geniş çapta ilgi görmese de, 1959’da açtığı ilk büyük sergiyle dünya çapında tanınmaya başladı. Hayranlarının büyük bir kısmını, onun eserlerinin matematik ilkelerini olağanüstü bir biçimde görselleştirdiğini fark eden matematikçiler oluşturuyordu.
MC Escher Kimdir?
1898’de Maurits Cornelis Escher adıyla doğan Escher, Hollanda’da varlıklı bir ailenin beş çocuğundan biriydi. Ailesi 1903 yılında Arnhem’e taşındı ve Escher burada okul hayatına başladı. Ancak bu yıllar onun için son derece zorlu geçti. Okul yaşamını daha sonra açıkça “cehennem” olarak tanımlayacaktı.

Ergenlik döneminde sanata yönelmesi, hayatında önemli bir kırılma noktası oldu. Bu ilgi ona ilk kez bir yön ve amaç duygusu kazandırdı. 1917’de arkadaşı Bas Kist ile birlikte, Hollandalı sanatçı Gert Stegeman’ın atölyesinde baskı çalışmaları üretmeye başladı.
Başlangıçta Haarlem Mimarlık ve Dekoratif Sanatlar Okulu’nda mimarlık eğitimi aldı. Ancak bir öğretmeninin yönlendirmesiyle grafik sanatlara geçiş yaptı. 1921’de ailesiyle yaptığı İtalya yolculuğu, doğaya olan ilgisini derinleştirdi. Ağaçlar ve peyzaj üzerine ayrıntılı çizimler yaptı ve bunları baskı tasarımlarına dönüştürdü.
Ertesi yıl İspanya’ya giderek Madrid, Toledo ve Granada’yı gezdi. Özellikle Granada’daki 14. yüzyıldan kalma Mağribi yapısı Elhamra Sarayı’ndaki İslami tekrar desenleri, onu derinden etkiledi ve sonraki çalışmalarının yönünü belirledi.

Elhamra’daki döşemelerin olağanüstü çeşitliliği ve geometrik karmaşıklığı, Escher’in teselasyonlara olan ilgisini ateşledi. Bu ilgi, en ünlü yapıtlarının önemli bir bölümünde doğrudan karşılık buldu.
MC Escher’in Çalışmalarında Öne Çıkan Matematik
Escher’in matematiğe duyduğu derin ilgi ve teknik kavramları görsel bir ustalıkla ifade etmesi, sanat dünyasında çeşitli eleştirilere neden oldu. Pek çok eleştirmen, onun çalışmalarını aşırı entelektüel ve duygudan yoksun buldu. Ancak buna rağmen eserleri geniş bir izleyici kitlesine ulaştı. Sonucunda bu ilgi günümüze kadar artarak sürdü.
Escher, yalnızca hayvan ve figür teselasyonlarıyla sınırlı kalmadı. Yineleme, çoklu boyutlar ve özellikle imkânsız yapılar üzerine yoğunlaştı. Relativity (1953) adlı eserinde, yerçekiminin üç farklı yönde işlediği yanılsamasını yaratan bir yapı tasvir eder. Ortaya, çelişkili bakış açıları ve fiziksel olarak olanaksız biçimde birbirine bağlanan merdivenler çıkar.

Relativity, 1954 yılında Amsterdam’da düzenlenen Uluslararası Matematikçiler Kongresi sırasında, Escher’in diğer yapıtlarıyla birlikte bir müzede sergilendi. Bu sergi, matematiksel fizikçi Roger Penrose ile Kanadalı geometri uzmanı Harold Coxeter’ın dikkatini çekti.
Escher’in taşbaskısından etkilenen Roger Penrose, babası Lionel Penrose ile birlikte imkânsız nesneler üzerine düşünmeye başladı. Lionel Penrose, hem psikiyatr hem de genetikçi ve aynı zamanda matematikçiydi. Baba-oğul, iki boyutta çizilebilen ancak üç boyutlu uzayda var olması imkânsız biçimlere odaklandılar.
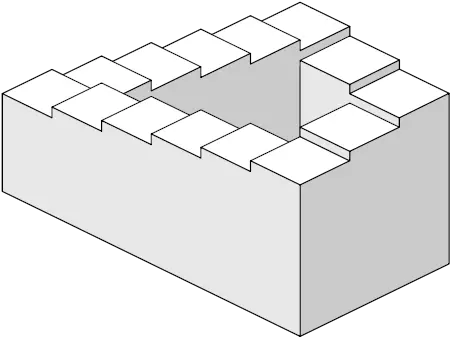
Amsterdam’daki kongreden birkaç yıl sonra Roger Penrose, Escher’e daha sonra “Penrose üçgeni” olarak anılacak olan imkânsız nesnenin çizimini gönderdi. Mektubuna ayrıca, babasının tasarladığı ve sonsuz bir döngüde yukarı ya da aşağı hareket ediyormuş izlenimi veren merdiven görselini de ekledi.

Bu fikir Escher’i doğrudan etkiledi ve harekete geçirdi. Ascending and Descending (1960) ile Waterfall (1961) adlı eserler bu esinle ortaya çıktı. Bu yapıtlarında Escher, figürleri ve suyu, sürekli olarak yükseliyor ya da alçalıyormuş gibi gösterdi. Ancak her hareket, sonunda başladığı noktaya geri dönerek imkânsız bir döngü oluşturuyordu.
Escher Ve Circle Limit
Müzedeki sergiyi gezen Harold Coxeter, Escher’in yeteneğini fark etti. Bunun üzerine, Amsterdam’daki kongrede sunduğu bildirinin bir kopyasını Escher’e gönderdi. Metin, Coxeter’ın kendi eliyle çizdiği bir diyagramı da içeriyordu.
Hiperbolik düzlem, herkesin aşina olduğu Öklid düzlemi gibi açık bir yapıya sahiptir. Ancak temel bir fark vardır. Bu düzlemde, paralel doğrular bazı yönlerde birbirine yaklaşırken, başka yönlerde birbirinden uzaklaşır. Hiperbolik düzlemin disk biçimindeki temsiline Poincaré diski adı verilir. Bu gösterimde, düzlem üzerindeki üçgen gibi şekiller diskin kenarına yaklaştıkça giderek küçülür ve bozulur.
Escher, Coxeter’ın çizimini incelediğinde, sonsuzluğu sınırlı bir iki boyutlu düzlemde temsil etmenin mümkün olduğunu hemen kavradı. Coxeter’la yaptığı ek görüşmelerin ardından, hiperbolik düzlemi daha karmaşık biçimlerle döşemeye başladı. Sonuç olarak, 1958–1960 yılları arasında Circle Limit I–IV başlıklı dört taşbaskıdan oluşan bir dizi ortaya çıktı.

Bu dizinin doruk noktası olan Circle Limit IV: Heaven and Hell adlı eserinde, beyaz melekler ve siyah şeytanlardan oluşan bir teselasyon, Poincaré diski üzerinde ustalıkla yerleştirilmiştir.
Sonuç Olarak
Escher, uzun yaşamı boyunca çoğunluğu siyah-beyaz olmak üzere 2000’den fazla çizim ve 448 taşbaskı ile ahşap gravür üretti. Eserleri, sanat ile matematiği birleştiren özgün yaklaşımı sayesinde geniş bir hayran kitlesi kazandı. Hollanda’nın Lahey kentinde yer alan Escher in Het Paleis müzesi, onun anısına kuruldu ve sanatçının çalışmalarını kalıcı olarak sergilemeye devam ediyor.

Escher, üretken kariyerinin son yıllarını, sağlık sorunları nedeniyle daha sakin bir tempoda geçirdi. 1970’lerin başında birkaç büyük sergi daha açtı ancak giderek azalan enerjisiyle birlikte sanat üretimi yavaşladı. 1972 yılında, 73 yaşındayken, hayatını kaybetti. Geride, sanat tarihinde silinmez bir iz bırakan bir miras bıraktı.
Kaynaklar ve ileri okumalar:
- To Create His Geometric Artwork, M.C. Escher Had to Learn Math the Hard Way. Yayınlanma tarihi: 2 Ekim 2023. kaynak site: Popular mechanics. Bağlantı: To Create His Geometric Artwork, M.C. Escher Had to Learn Math the Hard Way
- Lesso, Rosie. “M.C. Escher: Master of the Impossible” TheCollector.com, November 28, 2019, https://www.thecollector.com/m-c-escher-master-of-the-impossible/
Matematiksel





