Bir deste iskambil kâğıdını karıştırdığınızda, büyük olasılıkla eşi benzeri olmayan bir sıra oluşturursunuz. Yani, o dizilişi sizden başka hiç kimse yapmamıştır. Bu kulağa inanılmaz gelse de, kart karıştırmanın matematiği budur. 1990’ların sonlarında çevrimiçi bir poker oyunu geliştiren programcıların başına geldiği gibi, bu durum bazen beklenmedik sonuçlar da doğurur.

Kâğıt karıştırmanın matematiği aslında basittir. 52 kâğıdın kaç farklı şekilde dizileceğini bulmak için olası tüm sıralamaları düşünmek gerekir. İlk karta 52 farklı seçenek vardır. Bu kart seçildikten sonra, ikinci kart için 51, üçüncü için 50 seçenek kalır ve bu böyle devam eder.
Dolayısıyla 52 kâğıt 52 × 51 × 50 × … × 2 × 1 yani 52! farklı biçimde dizilir. Bu çarpımın sonucu 67 sıfırlı bir sayıdır. Bu sayı, Dünya’daki atom sayısından katrilyonlarca kez fazladır. Peki bu durumda, başka birinin seninle aynı dizilişi yapma olasılığı nedir?
Bu sorunun cevabı yalnızca 1 / 52! değildir; çünkü bu oran sadece belirli bir dizilişi tutturma ihtimalini gösterir. Asıl mesele, dünyadaki herhangi iki kişinin aynı anda bir desteyi karıştırıp tam olarak aynı dizilişi elde etme olasılığıdır.,
Bu soru, doğum günü paradoksunu ile aynı ilkeye dayanır: Bir sınıftaki bir öğrencinin belirli bir günde doğmuş olma olasılığı oldukça düşüktür. Otuz kişilik bir grupta bu olasılık 1 − (364 / 365)³⁰ ≈ yüzde 7,9’dur.
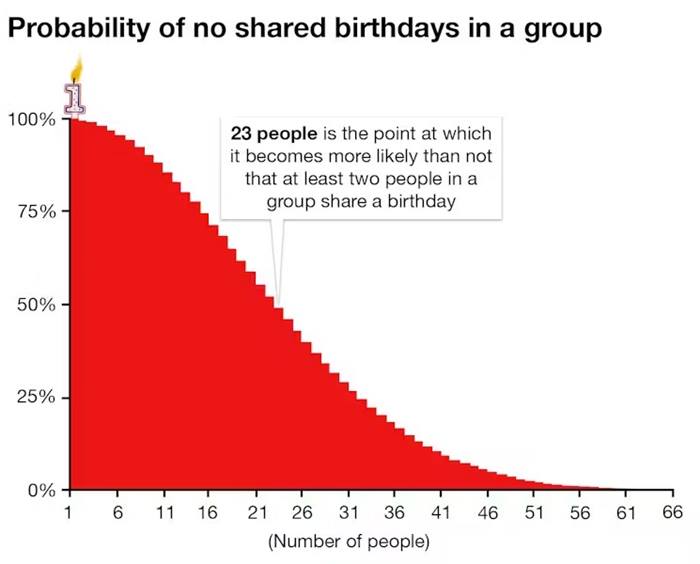
Ancak iki öğrencinin aynı gün doğmuş olma olasılığı oldukça yüksektir. Bu farkın nedeni, insanların genellikle sınıftaki olasılık çiftlerinin sayısını hafife almasıdır. Çünkü 30 öğrenciden yalnızca 30 değil, 435 farklı ikili oluşturulabilir. ( C(30, 2) = 30 × 29 / 2 = 435). Her ikili, “bu iki kişinin doğum günü aynı mı?” sorusu için ayrı bir olasılık oluşturur. Bu yüzden, iki kişinin aynı doğum gününü paylaşma ihtimali düşündüğünden çok daha yüksek çıkar.
Her Karıştırma Neden Olağanüstü Nadirdir?
Bir deste kartı dünyanın herhangi bir yerindeki biriyle aynı şekilde karıştırma olasılığını bulmanın birkaç yolu vardır. Bunlardan biri, önce bunun tam tersini hesaplamak ve sonucu 1’den çıkarmaktır.
İlk kişinin olasılığı 1’dir, ikinci kişinin olasılığı (52! – 1) / 52!, üçüncünün (52! – 2) / 52! şeklindedir ve bu böyle devam eder. Daha sonra bu sonucu 1’den çıkarırsın. Eğer dünyada sekiz milyar insan varsa, birkaç kişinin aynı kart dizilimini oluşturma olasılığı şu şekilde hesaplanır.
1 − ( (52! − 1) / 52! × (52! − 2) / 52! × (52! − 3) / 52! × … × (52! − 8 000 000 001) / 52! )
Burada, parantez içindeki çarpım tüm insanların kartları farklı biçimlerde karıştırma olasılığını temsil eder. Bu değeri 1’den çıkararak, en az iki kişinin aynı karıştırmayı yapma olasılığı elde edilir. Sonuç neredeyse sıfıra eşittir. Yani, sekiz milyar insan desteyi rastgele karıştırsa bile, iki kişinin tam olarak aynı dizilişi oluşturması matematiksel olarak neredeyse imkânsızdır.
Bu örnekle, dünyadaki birkaç kişinin bir desteyi karıştırarak tamamen aynı dizilişi oluşturmasının neredeyse imkânsız olduğunu gösterdik. Peki her insanın yaşamı boyunca yaklaşık 100 deste karıştırdığını varsayarsak sonuç değişir mi?
Kısa cevap, fark neredeyse yoktur. Eğer şimdiye dek yaşamış tüm insanları hesaba katarsak ve her birinin yaşamı boyunca ortalama 100 deste karıştırdığını varsayarsak, aynı dizilişin birden fazla kez oluşma olasılığı %0,0000…000000000000000000000000000000000000000000017’den (1.7 × 10−40 ) bile küçüktür.
Bu da şunu açıkça gösterir: İnsanlık tarihinin tamamında, iki kişinin bir desteyi tamamen aynı şekilde karıştırmış olma olasılığı neredeyse sıfırdır. Tabii bu, kartların gerçekten rastgele ve dikkatlice karıştırıldığını varsayarsak geçerlidir.
Kart Karıştırmanın Matematiğini Hafife Almayalım!
52! olasılığın büyüklüğü çevrimiçi oyun geliştiricileri için bir sorun yaratır. Çevrimiçi poker oyunlarında büyük miktarlarda para döndüğü için, bu oyunların güvenli olması, dijital kartların da iyi karıştırılmış ve rastgele dağıtılmış olması gerekir.
İdeal koşullarda bir algoritma, 52! olası diziliş arasından tamamen rastgele bir tanesini seçmelidir. Ancak hiçbir bilgisayar bu kadar büyük bir sayıyı depolayacak belleğe sahip değildir ve kusursuz bir rastgele sayı üreteci de henüz yoktur. Bu yüzden geliştiriciler, genellikle kart karıştırmayı yaklaşık olarak taklit eden algoritmalara başvurur.

1990’ların sonlarında ASF Software adlı bir yazılım platformu, Planet Poker gibi çevrimiçi poker sağlayıcılarına kart karıştırma algoritmaları sunuyordu. Platform, oyunun güvenilir biçimde programlandığını göstermek için algoritmayı web sitesinde bile paylaşmıştı. Bu paylaşım, Reliable Software Technologies adlı bir bilişim şirketinin çalışanlarının dikkatini çekti.
Algoritma, sıralı bir deste kartla başlıyor ve her adımda iki kartın yerini değiştiriyordu. Bunun için bilgisayarın sistem saatine bağlı bir rastgele sayı üretecisi kullanılıyordu. Ancak bu yöntemin ciddi kısıtları vardı.
Öncelikle, kart değiştirme mekanizması bazı dizilişlerin diğerlerinden daha sık ortaya çıkmasına yol açıyordu. Ayrıca sistem, sayı üretimini gece yarısından itibaren geçen saniyelere bağlamıştı ve her gün sıfırlanıyordu. Bu da olası rastgele değerleri ciddi biçimde sınırlıyordu. Reliable Software ekibi, bu yöntemle yalnızca yaklaşık 86 milyon farklı dizilişin üretilebildiğini ortaya çıkardı.

Programcılar, sistemin karıştırma işlemini rastgeleleştirmek için bilgisayarın saatine bağlı olduğunu fark edince, bu saat bilgisini de hesaba katarak kart dizilişlerini daha da dar bir aralıkta tahmin edebileceklerini anladı. Kendi yazılımlarını sistem saatine senkronladıklarında, olası dizilişlerin sayısı 200 bin civarına düştü.
Bu adımdan sonra olasılık kümesini taramak 90’ların basit bilgisayarları için bile çok kolaydı. Reliable Software çalışanları bu güvenlik açığını algoritmayı geliştiren ekibe bildirdi ve sorun giderildi.
Sonuç Olarak
Günümüzde birçok çevrimiçi poker sitesi, Fisher–Yates ya da diğer adıyla Knuth karıştırma algoritmasını kullanıyor. Uygulaması oldukça basit olan bu yöntem, gayet tatmin edici sonuçlar veriyor.
Elbette bu tür algoritmaların da sınırları var. Sonucunda rastgele sayı üreteçleri, gerçek bir deste kartla elde edilecek rastgeleliği tam anlamıyla sağlayamıyor. Yine de, en usta insan dağıtıcı bile her seferinde kusursuz bir el veremez.
Kaynaklar ve ileri okumalar
- How the Math of Shuffling Cards Almost Brought Down an Online Poker Empire. Kaynak site: Scientific American. Yayınlanma tarihi: 6 Temmuz 2025. Bağlantı: How the Math of Shuffling Cards Almost Brought Down an Online Poker Empire
- Kroese, Dirk & Brereton, Tim & Taimre, Thomas & Botev, Zdravko. (2014). Why the Monte Carlo method is so important today. Wiley Interdisciplinary Reviews: Computational Statistics. 6. 10.1002/wics.1314.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel