Matematikçiler ve psikologların yolları fazla sık kesişmez. Arada bir kesişse bile bunun Hanoi Kulesi gibi (görünüşte) mütevazı bir bulmaca içermesini beklemezsiniz. Hanoi kulesi (ayrıca Brahma kulesi veya Lucas kulesi olarak da adlandırılır) 19. yüzyılda Fransız matematikçi Édouard Lucas tarafından icat edildi. Lucas aslında, Fibonacci dizisi üzerine yaptığı çalışmayla tanınır. İlgili Lucas dizileri ve Lucas sayıları onun adını almıştır. ( Detaylar için: Fibonacci Sayılarının Kardeşi Lucas Sayıları İle Tanışalım)

Bu bulmacadaki amaç, sol tarafta üst üste duran diskleri, her seferinde bir disk hareket ettirmek kaydıyla, sağ tarafa taşımaktır. Bu sırada hiçbir disk, kendinden küçük olanın üstüne konulamaz. Mümkün olan en az hamle sayısıyla oyun tamamlanmalıdır. Hedefe ulaşmak için gereken hareketler, bir özyineleme örneğidir. İlk diskin taşınması bir hareket gerektirir, ancak sonraki her disk, önceki diskin iki katı hareket sayısı gerektirir.
Gerçekten de bu bulmaca her iki bilim dalında da kendine bir yer bulur. Psikolojide, birinin bilişsel yeteneklerini değerlendirmeye yardımcı olur. Matematiksel açıdan da bizleri henüz cevaplanmamış şaşırtıcı derecede zor sorulara yönlendirir.
Hanoi Kulesi Efsanesi

Bu bulmacanın icadının bir Hindu tapınağı efsanesi ile ilişkili olduğu düşünülmektedir. Efsaneye göre Brahma tapınağında 64 adet farklı boyutlarda altından diskler bulunmaktaymış. Tapınağı gelenlere, bir oyun oynayıp kuralına göre oyunu bitirirlerse, tüm bu altın diskleri götürebilecekleri söylenirmiş.

Altın disklerin birinci çubuktan üçüncü çubuğa aktarımını istiyorlarmış. Bunu yaparken de sadece bir şartları varmış: Birinci çubuktan üçüncü çubuğa diskleri taşırken büyük bir disk kendinden küçük diskin üzerine gelmeyecek.
Rahiplerin bildiği ama oyunu oynayanların bilmediği bu problemin çözümü için 18446744073709551615 hamle gereklidir. Diskleri saniyede bir oranında hareket ettirebilseler bile işi bitirmenin yaklaşık 585 milyar yıl süreceğini hesaplayabilirsiniz.
Sonu pek parlak değil aslında bu efsanenin. İnanışa göre 64 altın diskin yeri değiştiğinde geçecek süre aynı zamanda dünyanın sonunun habercisidir. Son altın diski koyan birileri olsa da, para yine mutluluk getirmeyecektir. Neyse ki 585 milyar yıl Dünya’nın sonu hakkında endişelenmek için gerçekten oldukça uzun bir zamandır.
Hanoi Kulesi Çözümü Nasıl Yapılır?
Bir disk ya da iki disk ile bu oyunu oynamanın anlamı yoktur. Çok kolaydır. Bir diskte tek hamlede işiniz biter. Sonuçta diski sadece soldan sağa taşırsınız. İki diskli oyunu ise üç hamle ile tamamlamak mümkündür. Bunun için küçük diski ortadaki kareye, büyük diski en sağdaki kareye yerleştirin ve küçük diski büyük olanın üzerine yerleştirerek oyunu bitirin. Ancak hamle sayısının üç olduğunu aklınızda tutun Bu önemli.
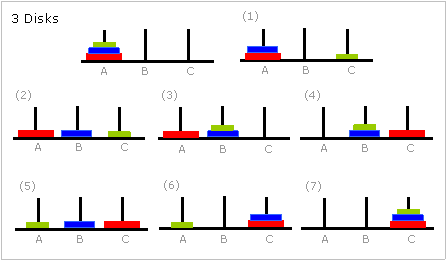
Oyunda 3 diskten itibaren belli kalıplar ortaya çıkmaya başlayacaktır. Aşağıdaki görselde de görebileceğiniz için elimizde üç diskimiz var ise bu problemi yedi adımda çözebiliriz.
Oyunu gittikçe daha fazla diskle oynadıkça, kalıbı daha net görebilirsiniz. Aslında bu sayede de oynamadan da oyunu tamamlamak için kaç hamle gerekeceğini hesaplayabilirsiniz. Üç diskli problemin çözümünde, ilk hamlenin, bir diskli problemin çözümü, üçüncü hamlenin de iki diskli problemin çözümü olduğuna dikkat edin. Üç disk problemi, yedi basamakta çözüldüğüne göre, dört disk problemini çözerken, yedinci basamakta üç disk problemini çözmüş olmalıyız. Şimdi dört disk için düşünelim.
Dört Veya Daha Fazla Disk İçin Gereken Zamanı Hesaplayalım
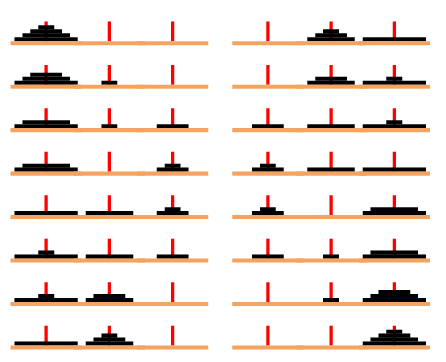
Önce yapmamız gereken ilk hamleyi bulmak. Bir diskte sağda, iki diskte ortada, üç diskte sağda başlamıştık. Öyleyse dört diskte ortada başlamalıyız. Çünkü en küçüğü ortaya alırsak, bir büyüğünü en sağa alıp, küçüğü de onun üstüne alarak, üç hamlede iki disk problemini çözmüş oluruz. Bundan sonra işlem üç disk problemini çözmek olur. Görseli incelersek sorunun 15 adımda çözülebildiğini görebilirsiniz.
İşi formüle döktüğümüz vakit ortaya çıkan ilginç bir algoritma olacaktır. Üç disk probleminde, ilk 3 hamle ile iki disk problemi çözülecektir. Sonucunda 1 hamle ile büyük disk hedefe konulmalıdır. Sonrasında da 3 hamle ile iki disk üstüne eklenmelidir. Bunun sonucunda da yapılan işlem sayısı 3 + 1 + 3 =7 dir.
Dört disk probleminin çözümü 15 hamlede gerçekleşti. Üç diski ortada toplamamız 7 hamle almıştır, bundan sonraki 1 hamle, dördüncü diske sağa almaktır. Sonraki hamle ise, 7 hamlede üç diski, bu en büyük diskin üzerine almaktır. Yani yapılan işlem sayısı 7 + 7 + 1 =15 tir.
Buradan yola çıkarak basit bir mantıkla beş disk için 31, altı disk için 63 hamle gerektiğini bulabiliriz. Bu aktarımı formüle dökersek 2n-1 elde ederiz. n yerine 64 sayısını yerleştirdiğimizde de yukarıda aktardığımız efsane için gerekli hamle sayısını yani 18446744073709551615 sonucunu hesaplarız.
Bunun Psikoloji İle İlgisi Nedir?
Psikologlar, özellikle hastaların önceden plan yapma ve bir görevi daha küçük parçalara ayırma yeteneklerini değerlendirmek için bir süredir Hanoi Kulesi’ni kullanıyorlar. Sonuçta bu oyunu bir kişiye açıklamak kolaydır. Bir kişinin her bir adımını izleyerek düşünme sürecini gözlemleyebilirsiniz. Ayrıca sadece bir disk ekleyerek ya da oyunun kurallarını revize ederek oyunu zorlaştırmak da mümkündür.
Problem çözme yürütücü işlevler sınıfına girdiğinden, Hanoi Kulesi testi ayrıca nöropsikolojide frontal lob aktivitesi veya bozukluğu ile ilişkili bilişsel eksiklikleri değerlendirmek için de kullanılır. Ancak oyunun tüm potansiyelinden yararlanmak biraz matematiksel uzmanlık gerekecektir. Matematikçilerin psikologlarla olan işbirliği yaptığı noktalardan birisi de bu testtir. Ayrıca göz atmak isterseniz: Phaistos Diski: Arkeolojinin En Büyük Gizemlerinden Biri
Kaynaklar ve ileri okumalar:
- Tower of Hanoi; Bağlantı: http://mathworld.wolfram.com/
- The Tower of Hanoi: Where maths meets psychology; Yayınlanma tarihi: 16 kasım 2012; Bağlantı: https://plus.maths.org/
- The Tower of Hanoi; yayınlanma tarihi: 26 kasım 2017; Bağlantı: https://www.scientificamerican.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel