Leonhard Euler, kuşkusuz tarihin en üretken matematikçisiydi. Sadece matematikte değil, fizik, astronomi, jeodezi, haritacılık, müzik ve gemi inşası gibi alanlarda da kapsamlı çalışmalar ve kitaplar yazdı. Üstelik bunları Latince, Fransızca ve Almanca olarak kaleme aldı.

Sadece çok yazmakla kalmadı; ilgilendiği her konuda olağanüstü bir yaratıcılıkla yeni fikirler ortaya koydu. Matematiğe yaptığı katkılar, yalnızca var olan alanları geliştirmekle kalmadı, aynı zamanda yepyeni alt disiplinlerin doğmasına da yol açtı
Örneğin fonksiyon kavramını tanıtan ve onu f(x) olarak yazan ilk kişi kendisidir. Ayrıca trigonometrik fonksiyonların modern gösterimi için de Euler’e teşekkür edebiliriz. Bugün, köşeleri A, B ve C harfleriyle işaretlenen ve bu köşelerin karşısındaki kenarlar için küçük harf a, b ve c’nin kullanıldığı üçgen gibi geometrik şekilleri etiketleme şeklimiz bile Euler’in çalışmaları sayesinde olmuştur.
Kısaca Leonhard Euler’in Hayatı

Euler, Basel’de bir papazın oğlu olarak dünyaya geldi. Gittiği okul onun yeteneklerini yeterince desteklemeyince, eğitimini babası üstlendi. 14 yaşında üniversitede felsefe dersleri dinlemeye başladı ve eğitimi, Descartes ile Newton’un fikirlerini karşılaştırdığı bir çalışma ile tamamladı. 16 yaşında babasının isteğiyle teoloji eğitimi aldı. Ancak babasının dostu olan Johann Bernoulli, onun sıra dışı matematik yeteneğini fark etti ve yönünü değiştirmesini sağladı.
Henüz 19 yaşındayken, Fransız Bilimler Akademisi’nin düzenlediği saygın bir yarışmada ikinci oldu. Yarışma, yelkenli gemilerde direklerin en verimli şekilde nasıl yerleştirileceğini konu alıyordu. O güne dek büyük deniz gemileri görmemiş olmasına rağmen, Euler bu alanda önemli bir çözüm önerisi sunmayı başardı. Daha sonra bu prestijli yarışmayı toplamda 12 kez kazanarak olağanüstü bir başarıya imza attı.
Basel’de boşalan bir fizik profesörlüğü için başvurdu ancak kabul edilmedi. Bunun üzerine, 1727 yılında Daniel ve Jakob Bernoulli’nin izinden giderek, Büyük Petro tarafından üç yıl önce kurulan Rusya Bilimler Akademisi’nde görev almak üzere St. Petersburg’a gitti. Burada tıp fakültesinde anatomi ve fizyoloji dersleri vermesi planlandı. Ancak kısa süre içinde, 1730’da fizik, 1733’te ise Daniel Bernoulli’nin yerine matematik profesörü oldu.
1734’te akademide çalışan İsviçre kökenli bir ressamın kızı Katharina Gsell ile evlendi. Bu mutlu evlilikten 13 çocukları oldu, ancak ne yazık ki sadece beşi hayatta kalabildi.
Euler bu sıralarda, sağ gözündeki görüşünü kendi deyimiyle aşırı çalışması nedeniyle 31 yaşında tamamen kaybetti. Bu yarı karanlık durum Euler’in çalışmalarını zerre kadar etkilemedi. Hatta ‘Artık dikkatimi dağıtacak daha az şey olacak’ diyerek durumu olgunlukla karşıladığını ifade etti.
Fiziksel Sorunları Euler’i Üretmekten Asla Alı Koymadı
1741 yılında Rusya’daki iç karışıklıklar nedeniyle Euler, St. Petersburg’dan ayrıldı. Berlin’e giderek Prusya Bilimler Akademisi’nin matematik sınıfı başkanlığını üstlendi. Akademinin ilk başkanı Pierre Louis Moreau de Maupertuis’ti. Euler, onun çalışmalarına aktif olarak destek verdi.

Berlin’de geçirdiği 25 yıl boyunca 380 bilimsel makale yazdı. Bununla da yetinmedi; gözlemevinin yönetimiyle ilgilendi, botanik bahçeleriyle ve Potsdam’daki Sanssouci Sarayı’nın su sistemiyle uğraştı. Euler, diferansiyel denklemlerin çözümüne getirdiği yöntemlerle fiziğe de yön verdi.
St. Petersburg’la bağlarını hiçbir zaman koparmadı. Özellikle arkadaşı Christian Goldbach ile uzun yıllar boyunca mektuplaştı. Birçok soruyu yanıtladı, bazıları ise yanıtsız kaldı. Bunlardan biri, 1742’de Goldbach’ın yazdığı ve hâlâ kanıtlanmamış olan şu ünlü önermeydi. “İki sayısından büyük her çift sayı, iki asal sayının toplamı olarak yazılabilir.” Günümüzde bu önerme Goldbach varsayımı adı ile bilinmektedir.
1766 yılında Euler yeniden St. Petersburg’a döndü.. Berlin’deki görevini Joseph-Louis Lagrange devraldı. Kısa süre sonra tamamen kör olmasına rağmen, çalışmalarına ara vermedi. Oğlu ve damadına dikte ederek 400’ün üzerinde yeni eser üretti.
Euler Bize Ne Miras Bıraktı?
Euler, yazdığı ders kitaplarıyla analiz alanının sistematik bir yapıya kavuşmasına büyük katkı sağladı. Bugün matematikte yaygın olarak kullanılan birçok kavram ve gösterimi ilk kez o tanımladı. “Fonksiyon” terimini ortaya koydu; trigonometrik fonksiyonların günümüzdeki adlandırmalarını o kullandı. Ayrıca f(x) gösterimi, toplam sembolü ∑ ve i sembolü de Euler’in katkıları arasındadır.

Euler aynı zamanda doğal logaritmanın tabanı olan e sayısını bu harfle simgeleyen kişidir. Bugün bu sayı “Euler sayısı” olarak anılır.
Euler, Jean d’Alembert (1717–1783) ile aynı dönemde karmaşık sayılarla cebirsel işlemleri geliştirdi ve karmaşık değişkenli fonksiyonları incelemeye başladı. 1743 yılında, karmaşık sayıların kuvvet serileriyle ifade edilmesini incelerken, trigonometrik fonksiyonlarla üstel fonksiyon arasında bugün onun adıyla anılan çarpıcı ilişkiyi keşfetti:
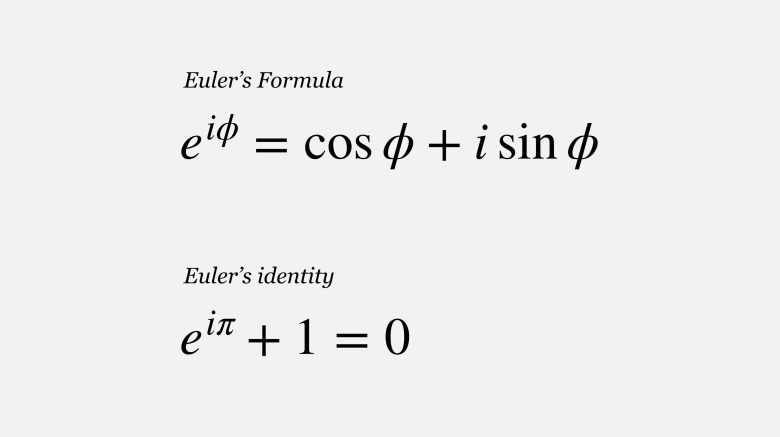
Bu basit denklem, matematiksel analizde, fiziksel dalga teorilerinde ve mühendislikte merkezi bir rol oynar. Euler’in bu formülü, karmaşık sayıların gücünü ve güzelliğini ortaya koyan en ikonik ifadelerdendir.
Euler, sayı teorisi alanında yalnızca keşifler yapmakla kalmadı, aynı zamanda öncellerinin çözemediği birçok soruya yanıt getirdi. Bunlardan biri Fermat’nın ortaya koyduğu ancak ispatlamadığı “Fermat’ın Küçük Teoremi“ydi. Euler, bu teoremin üç farklı ispatını geliştirdi. Bu esnada bugün kendi adıyla anılan Euler φ fonksiyonunu tanımladı.
Bu fonksiyon, n doğal sayısına, 1 ile n arasında olup n ile aralarında asal olan sayıların adedini atar. Örneğin, 10 ile 1, 3, 7 ve 9 aralarında asaldır; dolayısıyla φ(10)=4 olur. Euler bu fonksiyonun asal çarpanlara dayalı çarpım biçiminde ifade edilebileceğini gösterdi.
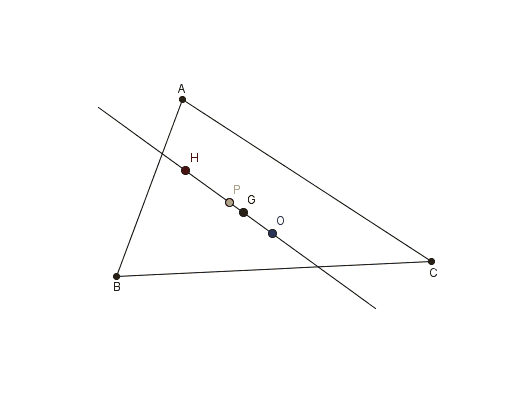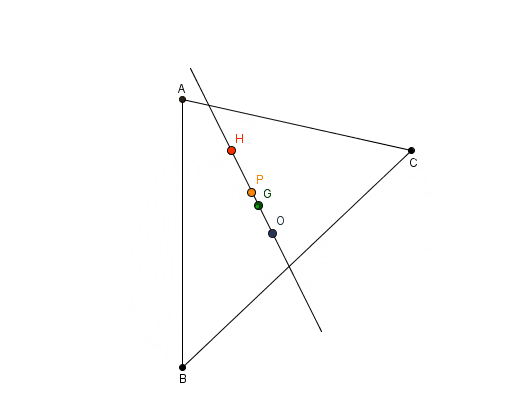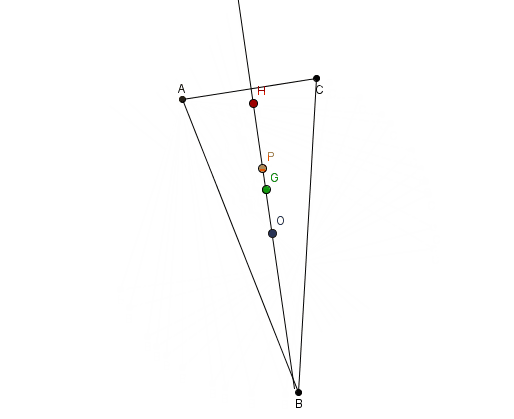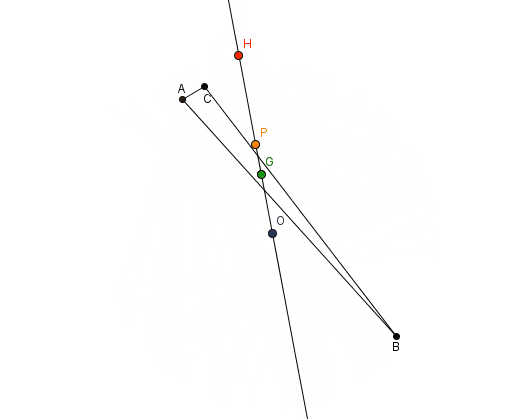
Geometriye de önemli katkılar yaptı. Bir üçgende kenarortayların kesişim noktası, yükseklerin kesişim noktası ve kenar ortayların kesişim noktası aynı doğru üzerindedir. Bu doğruya Euler Doğrusu denir. Ayrıca, bu doğrunun orta noktası merkez kabul edilerek çizilen çember, üçgenin yüksek ve kenar ortay ayak noktalarından geçer. Bu çember de Euler Çemberi olarak bilinir.
Sonuç Olarak
Euler, son derece alçakgönüllü bir insandı. Laplace’ın dediği gibi, o dönemin tüm matematikçileri için gerçek bir öğretmendi. 19. yüzyılın birçok önemli matematiksel gelişmesi, doğrudan ya da dolaylı olarak Euler’in çalışmalarından esinlenmiştir.
Hayattayken, eserlerinin ölümünden sonra ancak 20 yılda toparlanabileceğini söylemişti. Ancak bu süreç beklentilerin de ötesine geçti: Euler’in tüm çalışmalarını derleyip yayımlamak tam 47 yıl sürdü. Euler, 1783’te hayatını kaybettiğinde arkasında 866 bilimsel çalışma bırakmıştır. Pierre-Simon Laplace, onun bu eşsiz mirasını şu sözlerle özetler: “Euler’i okuyun, Euler’i okuyun. O hepimizin ustasıdır.”
Kaynaklar ve ileri okumalar
- Alfred S. Posamentier and Christian Spreitzer; The Lives and Works of 50 Famous Mathematicians
- Leonhard Euler, Mathematician: His Life and Work. Yayınlanma tarihi: 3 Ekim 2018. Bağlantı: Leonhard Euler, Mathematician: His Life and Work
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





