Birçok Yunan matematikçi kendilerini konik kesitlerin incelenmesine adamıştır. Ancak günümüzde kullanılan konik kesitlerin tanımları on dokuzuncu yüzyılda Germinal Pierre Dandelin tarafından kanıtlanmıştır. Bunu yapmayı da Dandelin Küreleri sayesinde başarmıştır.
Günlük yaşantımızda çemberlerden sık sık söz ederiz. Ancak hayatımızın her günü çemberlerden çok daha fazla elips görürüz. Bir bardağa tepeden baktığımız zaman bardağın ağzını bir çember biçiminde görürüz. Ancak yandan baktığımızda göreceğimiz şekil hemen hemen bir elipstir.
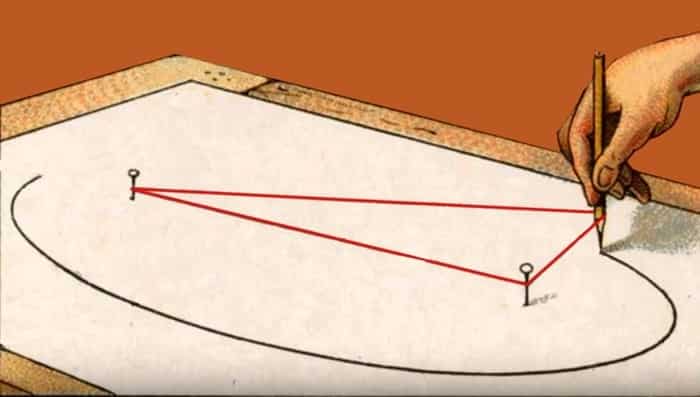
Elips çizmenin en bilinen yöntemi, bir düzleme iki çivi çakmak ve bu çivilere bir ip bağlamaktır. Kalemi ipe geçirip bir tur çevirdiğimizde ortaya elips çıkar. Öte yandan Antik Yunanlılar daha geometrik bir tanım verirlerdi. Onlar bir koniyi bir düzlemle keser, böylece oluşan ara kesitin elips olduğunu söylerlerdi. Birbirinden çok farklı gibi görünen bu iki tanım nasıl eşdeğer olabilir?
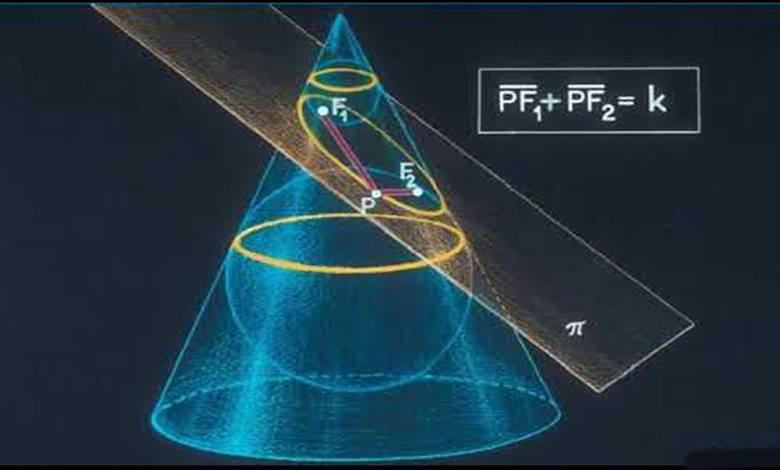
Bu sorunun cevabı 1822’de Belçikalı mühendis Germinal Pierre Dandelin (1794–1847) tarafından verilecekti. Kendisi bir elipsin iki görüntüsünü (a) bir koninin enine kesiti veya (b) PA + PB’nin sabit olduğu bir eğri ilişkilendirmenin yeni bir yolunu keşfetti. Bunu iki küre sayesinde gerçekleştirdi. Bu küreler günümüzde Dandelin Küreleri olarak biliniyor. Ancak öncelikle elipsin ne olduğunu bir anımsayalım.
Elips Nedir?
1.Tanım: Sabit iki noktaya uzaklıkları toplamı sabit olan noktaların kümesi bir elipstir. En başta da söylediğimiz gibi bu tanım, elips çizmek için sık sık kullanılır. F1 ve F2 noktalarına bağlanan bir ip, gergin tutularak bir tur attırıldığında P noktası bir elips çizer.
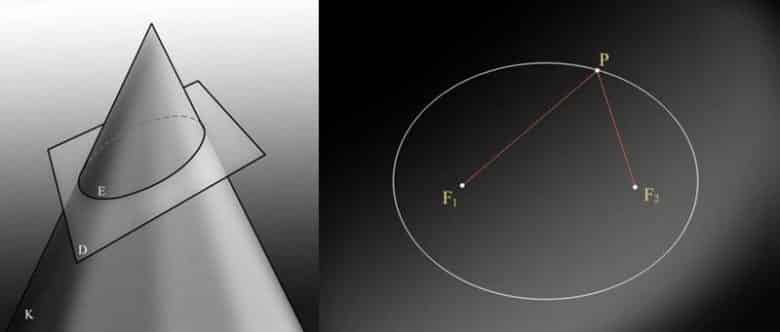
2. Tanım: Bu tanım, Apollonus ve Eucleides gibi antik çağ matematikçilerinin kullandığı geometrik özelliklere dayanır. Buna göre bir koni ile bir düzlemin arakesiti daima bir koniktir. Eğer düzlemin yatayla yaptığı açı, koninin doğrultmanının yatayla yaptığı açıdan küçükse, bu konik “elips” adını alır. Ancak bu tanımda akla gelmesi gereken bir soru asimetrik bir kesimin neden ve nasıl simetrik bir şekil oluşturduğudur.
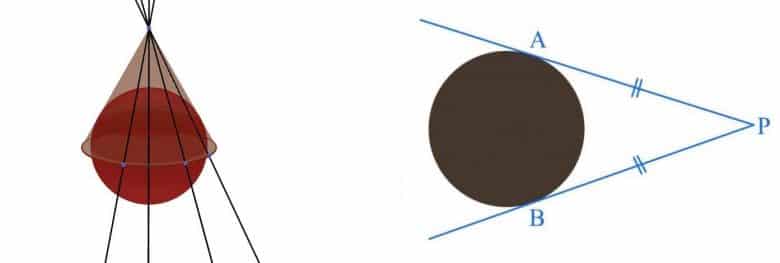
Konuya devam etmeden önce belleğimizi tazeleyelim. Düzlemde bir daireye dışındaki bir P noktasından çizilen iki teğet parçası eşit uzunluktadır. Bunu küreye de uygulayabiliriz. Bir küreye dışından çizilen teğet parçaları eşit uzunluktadır.
Dandelin Küreleri Nelerdir?
Şimdi gelelim eşdeğerliliğin nasıl bulunduğuna. D düzlemi ile K konisinin ara kesiti, odakları F1 ve F2 olan elips olsun. Koniye ve elipse teğet olan iki tane küre vardır. Dandelin küreleri diye tanımlanan bu küreler M1 ve M2 merkezli kürelerdir. Şimdi, elips üzerinde herhangi bir P noktası alalım.
T noktası K konisinin tepe noktası olmak üzere, [PF1] doğru parçasının [PR] doğru parçasına eşit olduğunu görünüz. Bunun nedenini anlamak için P noktasının hem elips, hem de koni üzerinde olduğunu anımsamamız gerekiyor. Dolayısıyla P’den küreye çizilen teğet parçaları eşit olacaktır. Çünkü küre hem elips düzlemine hem de koniye teğettir.
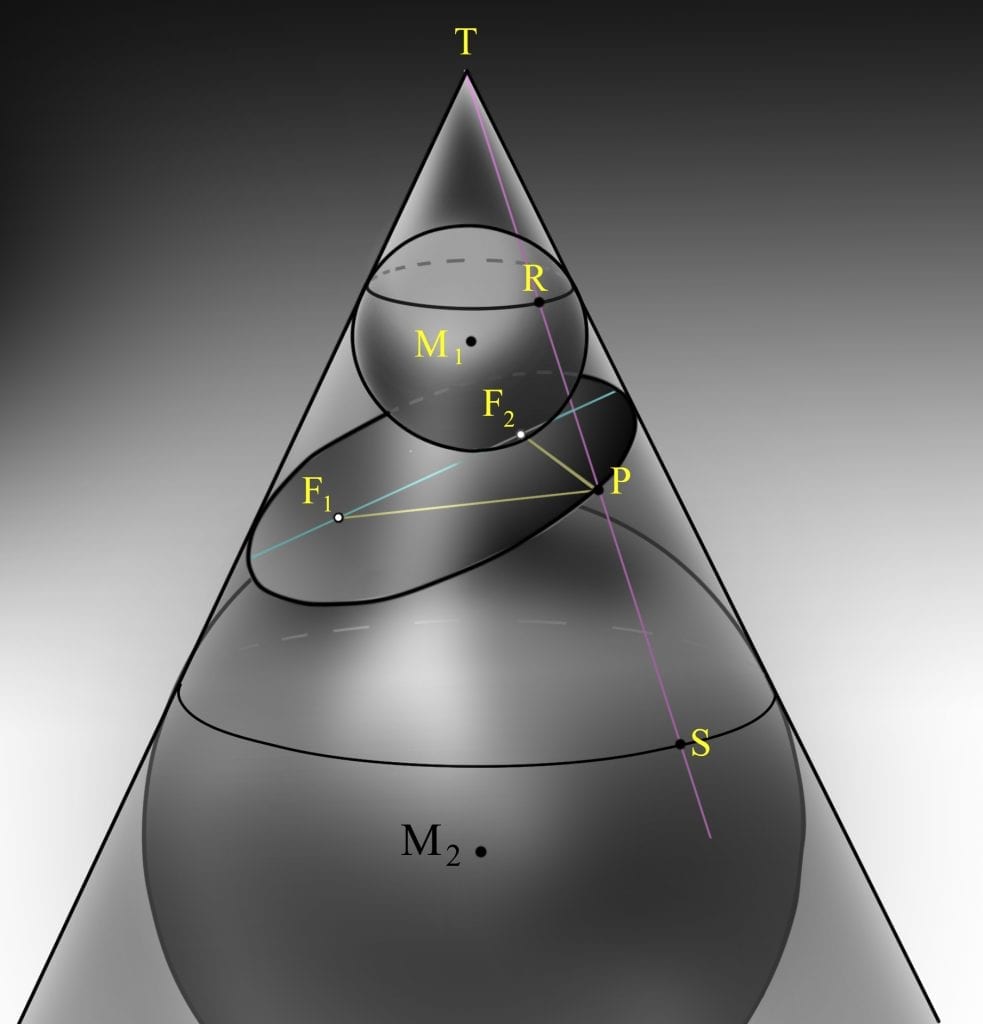
kürelerdir.
Benzer şekilde, [PF2] doğru parçası da [PS] doğru parçasına eşittir. Burada, R ve S noktaları TP doğrusunun, [M1] ve [M2] merkezli küreleri kestiği noktalardır. Şimdi ispatımız tamamlanıyor. E elipsi üzerinde alınan her P noktası için, |PF1|+|PF2| toplamı sabittir, çünkü: |PF1| + |PF2| = |PR|+|PS| = |RS| olur. Zaten kanıtlamak istediğimiz de buydu. (|RS| uzunluğunun sabit olduğunu görünüz.)
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





