
Yüzyıllar boyu matematikçiler doğanın tasarım ustalığını açıklayan bir dizi kural bulmayı ummuşlardır. İşte bu umudun peşinde koşarken karşılarına sabun köpükleri ve onları anlamamızı sağlayan Plateau Kanunları çıkmıştır.
Sabun köpükleri sabunlu suyun içi boş bir küre oluşturacak şekilde havayı çevrelemesiyle oluşur. Yanardöner bir yüzeye sahip olan son derece ince tabakalardır. Sabun moleküllerinin katmanları arasındaki su buharlaştığında kendiliğinden er yada geç patlarlar. Bunun bir alternatifi aşağıda gördüğünüz gibi soğuk bir havada sabun köpüğü oluşturmaya çalışmaktır.

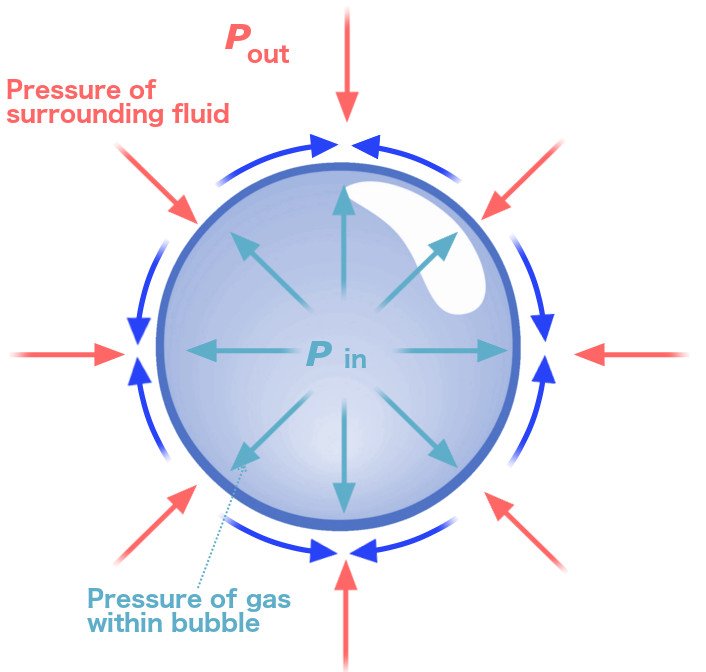
Bir sabun köpüğünün şeklini anlamanın anahtarı yüzey gerilimidir. Yüzey gerilimi, bir sıvının molekülleri arasındaki kohezif (çekici) kuvvet nedeniyle ortaya çıkar. Bir sıvı molekülü etrafındaki değer moleküller tarafından her yönden eşit olarak çekilir.
Bu nedenle üzerine etki eden net kuvvet sıfırdır. Ancak yüzeyde, moleküller sadece yanlara ve aşağıya doğru çekilir. Bu durumda da sıvının yüzeyi esnek bir zar görünümünde olur. Suya suya sabun eklediğiniz zamanda da yüzey gerilimi azalır ve hava bu sabunlu su katmanında hapsolur. Ve sabunlu su katmanı her zaman küresel bir form alır.
Sabun Köpükleri Küre Dışında Başka Bir Şekil Alamaz mı?
Üçgen ya da kare biçimli bir baloncuk yaratabilseydik izlemesi keyifli olabilirdi ama bu mümkün değildir. Doğadaki her şey gibi, sabun köpükleri de mümkün olan en düşük enerjiyi harcayacak biçimde olma eğilimi gösterirler. Yüzeydeki gerilimi en aza indirmek için de hacmi çevreleyen yüzey alanını azaltmak gerekir.
Küreden başka hiçbir şekil, daha küçük bir yüzey alanına sahip belirli bir hacmi kapsamaz. Bunu şöyle açıklayabiliriz. Elimizde hacmi santimetreküp olan bir olan bir küremiz ve aynı hacimde beş Platonik katımız olsun. Küremizin yüzölçümü 48.4 santimetrekare olacaktır.
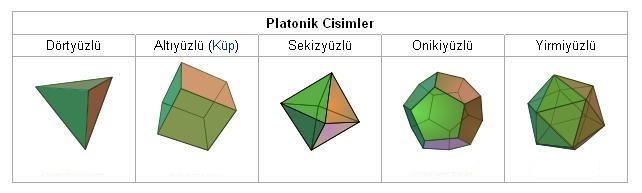
Oysa ki tetrahedron (4 yüzlü) 71.1, küp (6 yüzlü) 60.0, oktahedron (8 yüzlü) 57.2, Dodekahedron ( 12 yüzlü) 53.2 ve ikosahedron (20 yüzlü) 51.5 santimetre kare yüzey alanına sahip olacaktır. Sonucunda dikkat ettiyseniz şeklimiz küreye yaklaştıkça yüzey alanı küçülmektedir.
Baloncukların neden küreler olduğunun mantığını ve fiziği takip etmek zor değildir. Ancak kürenin belirli bir hacim için minimum alana sahip yüzey olduğunu matematiksel olarak kanıtlamak şaşırtıcı derecede zordur. Aslında tam bir kanıt 1884 gibi yakın bir tarihte gelmiştir. Bunu anlamak için öncelikle biraz tarihe yolculuk yapmak gerekir.
Kraliçe Dido Problemi
Roma mitolojisine göre Dido, Sur şehrinden Fenikeli bir prensestir. Kral olan kardeşi, kocasını öldürdüğünde şehirden kaçar ve Kuzey Afrika’da, ileride Kartaca adını alacak olan yere ulaşır. Bu bölgenin kralı, onun ve insanlarının yerleşebilmeleri için toprak satın almalarına izin verir. Fakat bu toprak yalnızca bir öküz derisinin kaplayabileceği büyüklükte olmalıdır.
Bunun üzerine Dido kendisine verilen deriyi ince şeritler halinde kestirip bunları birbirine bağlatır ve uzun bir kordon elde eder. Sıra bu kordonu, en geniş alanı kaplayacak şekilde yere yaymaya gelmiştir. Dido’nun şu problemle karşı karşıyadır artık: Kapalı eğriler arasında, en geniş iç bölgeye sahip olanı bulmak.

Anlatılanlara göre, Dido doğru seçimi kısa zamanda yapmış ve eşit çevre uzunluğuna sahip düzlemsel şekiller arasında en fazla alanın daireye ait olduğunu görmüştür. Ancak matematikçiler için bu iş o kadar kolay olmaz.
Yukarıda aktardığımız problem çözüldüğümü çözülemedi mi emin olamasak da Dido problemi 19. yüzyılını başında Jakob Steiner’ın konuyu ele almasına kadar tam olarak cevaplanamamıştı. Devamında başka matematikçiler Steiner tarafından ortaya atılan fikirleri geliştirdiler. Sonucunda Belçikalı fizikçi Joseph Plateau konu ile ilgili bir dizi yasa geliştirdi.
Plateau Kanunları Nedir?

Plateu’nun yaptığı deneysel çalışmalar onu dört basit sonuca ulaştırmıştı.
- Bir sabun köpüğünün zarı düzgün parçalar topluluğundan oluşur.
- Her bir düzgün parçanın ortalama eğriliği (yani yüzeylerinin ortalama eğimi) sabittir.
- Üç sabun baloncuğunun yüzeyleri, birleştikleri yerde düzgün bir eğri meydana getirir ve 120 derecelik bir açıyla her bir yüzeyi böler.
- Ortaya çıkan altı eğri birbirlerine yaklaştıkları yerde bir nokta oluştururlar ve bu noktada her çift eğri arasındaki açı eşittir (yaklaşık 109 derecedir).
Bu kurallar dizisi, ne kadar karmaşık olurlarsa olsun, tüm sabun baloncuklarının geometrik özelliğini açıklamaktadır. Plateau kendi kurallarına aykırı düşen baloncuk bulmak için çok uğraşmıştı. Ancak her seferinde elde ettiği sonuçlar, ortaya koyduğu kurallarla tam bir uyum göstermişti. Kısacası sabun köpükleri, her koşulda minimal alanı kaplayan doğanın harika oyuncaklarıydı. Ayrıca göz atmanız için: Sabunun Ardındaki Kimya: Sabun Kiri Nasıl Temizler?
Kaynaklar ve İleri Okumalar:
- Queen Dido’s problem; https://undergroundmathematics.org/
- Why Are Bubbles Round?; Yayınlanma tarihi: 8 Temmuz 2022; Bağlantı: https://www.scienceabc.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









