Alan Turing, 1936’da Turing makinelerini icat ettiğinde, aynı zamanda modern bilişimi de icat etmiş oldu.

Hesaplama, çoğumuzun sezgisel olarak anladığı bir kavramdır. Örneğin, f(x) = x + 3 fonksiyonunu ele alalım. x’in değeri 3 olduğunda, f(3) = 3 + 3 olur. Sonuç 6’dır. Bu fonksiyonun hesaplanabilir olduğu açıktır. Ancak bazı fonksiyonlar o kadar basit değildir ve hesaplanıp hesaplanamayacaklarını belirlemek kolay değildir. Yani, asla kesin bir sonuca ulaşamayabilirler.
1928’de Alman matematikçiler David Hilbert ve Wilhelm Ackermann, Entscheidungsproblem (“karar problemi”) adı verilen bir soru ortaya attılar. Zamanla, bu soru hesaplanabilirliğin resmi bir tanımına yol açtı. Bu tanım, matematikçilerin yeni tür problemleri çözmelerini sağladı ve kuramsal bilişimin temelini attı.

Bu tanım, 1936’da henüz 23 yaşında bir lisansüstü öğrencisi olan Alan Turing tarafından getirildi. Turing, yazdığı çığır açıcı makalede yalnızca hesaplama kavramını resmileştirmekle kalmadı, aynı zamanda matematikte temel bir soruyu çözdü.
Turing’in büyük öngörüsü, hesaplama sorusuna soyut bir makine biçiminde somut bir yanıt sunmaktı. Bu makineye daha sonra, doktora danışmanı Alonzo Church tarafından Turing makinesi adı verildi. Fiziksel bir cihaz olarak var olmayan bu makine, hesaplamanın kavramsal bir modelidir. Eğer bir fonksiyon Turing makinesi tarafından hesaplanabiliyorsa, o fonksiyon hesaplanabilir kabul edilecektir.
Turing Makinesi Nasıl Çalışır?
Bir Turing makinesi, sonsuz uzunluktaki bir bant üzerindeki sembolleri okuyup değiştirir ve bunu belirli bir kurallar tablosuna göre yapar. Bant, her biri tek bir sembol tutabilen hücrelerden oluşur.
.
Tablodaki her kural, makinenin mevcut durumu ve okuduğu sembole göre ne yapması gerektiğini belirler. Makine, bir son duruma ulaşır. (“kabul durumu” veya “reddetme durumu”). Böylece çalışmayı durdurur ve girdiyi kabul eder veya reddeder. Alternatif olarak, sonsuz bir döngüye girerek banttaki veriyi sonsuza kadar okumaya devam eder.
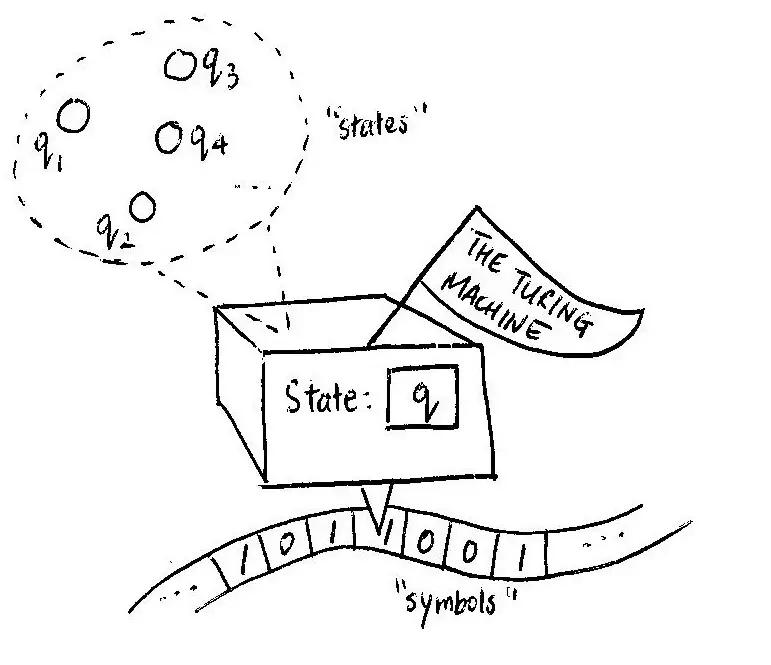
Turing makinesini anlamak için basit bir örnek düşünelim. Örneğin, bir girdinin sıfır olup olmadığını belirlemek isteyen bir Turing makinesi hayal edelim.
Makinenin okuduğu bant, boşluklar (#) ile çevrili sayılardan oluşur. Örneğin, girdimiz 0001 olsun ve bantta şu şekilde temsil edilsin: “#0000#”. Makine, ilk durumu olan q0’da başlar ve banttaki en soldaki hücreyi okur. Burada boş bir sembol (#) bulur. Kurallarına göre, makine boşluğu değiştirmez, bir hücre sağa hareket eder ve q1 durumuna geçer.
Artık makine ikinci hücrede ve 0 rakamını okuyor. Kurallarına tekrar bakar ve şu kuralı bulur: “q1 durumunda kal ve bir hücre sağa hareket et.” Makine kuralı uygular ve okumaya devam eder, tüm 0’ları geçerek 1 rakamına ulaşana kadar sağa gider.
1 rakamına ulaştığında, tablosuna bakar ve yeni bir kural bulur: “Eğer 1 sembolüyle karşılaşırsan, q2 durumuna geç.” q2, “reddetme” durumudur, yani makine burada durur ve “Hayır” yanıtını verir. Yani, “0001 sıfır mı?” sorusunun cevabı hayırdır, çünkü girdide 1 bulunmuştur.
Eğer giriş 0000 olsaydı, yani bant #0000# şeklinde temsil edilseydi, makine bütün 0’ları geçtikten sonra tekrar # sembolüne ulaşacaktı. Kurallar tablosuna göre, makine 0’ları okuduktan sonra # ile karşılaşırsa, q3 durumuna geçer. q3 “kabul” durumudur, yani makine “Evet” yanıtını verir.
Bilgisayarların Sınırı Nedir?
Turing, bu soyut makineyi kullanarak Entscheidungsproblem’e, yani karar problemine bir hesaplama modeliyle yanıt verdi. Bu problem temel olarak şunu sorar. Belirli bir matematiksel aksiyom kümesi verildiğinde, her zaman bir ifadenin doğru olup olmadığını belirleyebilecek mekanik bir süreç (bugün “algoritma” dediğimiz talimatlar dizisi) var mıdır?

Bu soruya Turing’in yanıtı, böyle bir algoritmanın her zaman var olmadığını göstermekti. Yani, bazı problemler hesaplanamazdır ve bilgisayarlar her matematiksel soruya cevap veremez. Turing’in bu keşfi, modern bilgisayar biliminin temel taşlarından biri haline geldi.
Ancak 1936 yılında, Alonzo Church ve Alan Turing, farklı yöntemler kullanarak, Entscheidungsproblem’in her durumda genel bir çözümünün bulunmadığını bağımsız olarak kanıtladılar. Örneğin, John Conway’in Hayat Oyunu (Game of Life) gibi bazı oyunlar karar verilemezdir. Yani, hiçbir algoritma başlangıçtaki bir desenin ilerleyen adımlarda belirli bir şekle dönüşüp dönüşmeyeceğini kesin olarak belirleyemez.
Turing, bir fonksiyonun ancak bir algoritma tarafından yürütülebiliyorsa hesaplanabilir olduğunu gösterdi. Aynı zamanda, bir algoritmanın bir Turing makinesi ile tanımlanabilen bir süreç olduğunu da kanıtladı. Dolayısıyla, hesaplanabilir bir fonksiyon, onu hesaplayabilen bir Turing makinesine sahip olan fonksiyondur. Bu tanım karmaşık görünecektir. ncak elimizdeki en iyi tanımlardan biridir.
Evrensel Turing Makinesi ve Modern Bilgisayarların Doğuşu
Bu gelişmeler, Kurt Gödel’in matematiğin eksik olduğunu kanıtlamasından yalnızca birkaç yıl sonra geldi. Church ve Turing, bazı matematiksel problemlerin çözülemez olduğunu, yani hiçbir algoritmanın bir ifadenin doğru mu yanlış mı olduğunu belirleyemeyeceğini gösterdi. Bu sonuç, David Hilbert için büyük bir darbe oldu. Hilbert, tüm matematiksel problemlerin kusursuz ve sistemli bir şekilde çözülebileceğine inanıyordu.
Turing’in makinesi yalnızca kuramsal matematiğe katkı sağlamakla kalmadı, aynı zamanda modern bilgisayarların gelişmesine de doğrudan yol açtı. Bunun temelini, evrensel Turing makinesi adı verilen bir varyant oluşturdu. Evrensel Turing makinesi, herhangi bir başka Turing makinesini ve herhangi bir girdiyi simüle eder.. Bugünkü bilgisayarlar gibi, herhangi bir programı okuyup çalıştırabilir ve aynı çıktıyı üretir.
1945 yılında, John von Neumann, evrensel Turing makinesi kavramını gerçek bir makinede mümkün kılan bir bilgisayar mimarisi önerdi. Von Neumann mimarisi, modern bilgisayarların temelini oluşturan ilkelerden biridir.
Bir diğer önemli ve giderek daha faydalı hale gelen Turing makinesi varyantı, olasılıklı Turing makinesidir. Standart bir Turing makinesi her girdi için belirli bir tepki verir. Oysa ki, olasılıklı bir Turing makinesi aynı girdiye birden fazla farklı tepki verebcektir. Belirli olasılıklarla farklı sonuçlar üretir.
Şaşırtıcı bir şekilde, bazı problemler için olasılıklı bir yaklaşım, deterministik (kesin) yaklaşımlardan daha verimlidir. Olasılıklı Turing makinelerinden esinlenen yaklaşımlar kriptografi, optimizasyon ve makine öğrenimi gibi birçok alanda pratik olarak kullanışlıdır.
Sonuç Olarak
Turing makineleri, modern bilgisayar biliminin temel taşlarından biridir. Ancak daha da önemlisi, temel sorular sormanın bilimin ilerlemesinde ne kadar kritik bir rol oynadığını göstermektedir. Church ve Turing’in çalışmaları yalnızca matematikte devrim yaratmakla kalmadı, aynı zamanda bilgisayar teknolojisinin doğmasını sağladı. Günümüzde kullanılan tüm hesaplama sistemleri, bu soyut makinelerin ortaya çıkardığı prensiplere dayanıyor..
Kaynaklar ve İleri Okumalar:
- The Most Important Machine That Was Never Built. Yayınlanma tarihi: 3 Mayıs 2023. Kaynak site: Quanta Magazine. Bağlantı: The Most Important Machine That Was Never Built
- Computers, maths and minds; Yayınlanma tarihi: 4 Şubat 2014; Bağlantı: https://plus.maths.org/
- Lucas, Salvador. (2021). The origins of the halting problem. Journal of Logical and Algebraic Methods in Programming. 121. 100687. 10.1016/j.jlamp.2021.100687.
Matematiksel





