Matematik tarihi boyunca Srinivasa Ramanujan’a uzaktan yakından benzeyen hiç kimse olmadı. Belki de bu nedenle hakkında uzun metrajlı bir film çekilen ender matematikçilerden oldu. Hindistan’da doğup 32 yaşında ölen Ramanujan’ın, günümüzde de matematiği şekillendirmeye devam eden fantastik fikirleri vardı.

2011 yılının Ocak ayında bir öğleden sonra, Hüseyin Murtada masasından kalktı ve odasında dans etmeye başladı. Matematikçi, birkaç ay önce bitirdiği doktora tezini yazarken kafasına takılmış bir fikri nihayet doğrulayabileceğini fark etmişti.
Matematikte tekillikler adı verilen özel noktaları inceliyordu ve birdenbire bu tekillikleri kanıtlamanın bir yolunu bulmuştu. Yapının içinde bir asır önce Srinivasa Ramanujan tarafından ilk kez yazılmış gizemli matematiksel ifadeler gizliydi.

Srinivasa Ramanujan Kimdir?
Srinivasa Ramanujan, 22 Aralık 1887’de, Hindistan’ın Tamil Nadu kentinde doğdu. Matematiğe ilgisi 12 yaşındayken başladı. O yıl eline geçen S. L. Loney’nin trigonometri kitabı, onun için bir dönüm noktası oldu.
Sonrasında, G. S. Carr’ın Synopsis of Elementary Results in Pure and Applied Mathematics (Soyut ve Uygulamalı Matematikte Temel Bilgiler Özeti) adındaki bir kitaba denk geldi. Kitap aslında bir ders kitabıydı ve ispatlara girilmeden binlerce sonuç, formül ve denklem içeriyordu. Kuramsal matematiği ilk kez bu kitaptan öğrenen Ramanujan, hayatı boyunca belki de bu nedenle, bir ispat yapma ihtiyacı duymadı.

Ancak ilgisi yalnızca matematiğe yönelmişti; diğer derslerle pek ilgilenmedi. Bu nedenle üniversitedeki Fellow of Arts sınavını birkaç kez denedi ama geçemedi; son denemesi 1907’deydi. Bu başarısızlığından sonra Ramanujan, birkaç yıl boyunca yoksulluk içinde yaşadı ve tüm zamanını kendi teoremlerine adadı.
1910 ile 1912 yılları arasında Ramanujan, Madras’ta (bugünkü Chennai) öğrencilere özel dersler verdi ve ardından küçük bir kâtiplik işi buldu. Bu dönemde bazı Hintli matematikçilerle tanıştı; onlar onun olağanüstü yeteneğini hemen fark ettiler. ,
Ramanujan kısa süre sonra Madras Üniversitesi’nde özel bir araştırma görevi elde etti. Böylece hem maddi durumu iyileşti hem de yeteneğini daha sistemli biçimde geliştirme fırsatı buldu
1913 yılında Ramanujan’ın defterleri, yüzlerce özgün teoremle doluydu. O sıralarda ona, çalışmalarını İngiltere’deki tanınmış matematikçilerle paylaşması tavsiye edildi. Ramanujan birkaçına mektup gönderdi, ancak ilk iki matematikçi notlarını hiçbir yorum yapmadan geri gönderdi.
Ellerindeki formüller onlara saçma gelmişti. Örneğin, onun bir denkleminde 1 + 2 + 3 + … = –1/12
sonucuna ulaştığını gördüler. Ramanujan, bu sonucun kendi kuramı içinde geçerli olduğunu vurgulamış olsa da, bu açıklama yeterince ikna edici bulunmadı.
Srinivasa Ramanujan’ın Hardy İle Buluşması

Üçüncü olarak mektup gönderdiği İngiliz matematikçi, ünlü sayı kuramcısı Godfrey Harold Hardy’ydi. Hardy, Ramanujan’ın çalışmalarındaki özgünlük ve dehayı fark etti; temkinli ama cesaret verici bir yanıt verdi. Kendi başına bir matematik devi olan Hardy’nin, matematiğe en büyük katkısının Ramanujan’ı keşfetmek olduğunu söylediği söylenir.
Bunun sonucunda Ramanujan, 1914’te İngiltere’ye giderek Cambridge Üniversitesi’nde çalışmaya başladı. 1914 ile 1919 yılları arasında orada kalarak Hardy ve onun çalışma arkadaşı John Edensor Littlewood ile birlikte araştırmalar yaptı. 1915 yılında tek başına ya da ortak yazar olarak dokuz makale yayımladı.

Neredeyse üç yıl boyunca işler son derece iyi gitti. 1916’da Ramanujan Cambridge’den lisans derecesini aldı. Hardy’nin büyük yardımıyla, birbiri ardına mükemmel makaleler yayınladı. Kısa bir süre sonra da Royal Society of London’ın bir üyesi seçilerek hayatının en büyük onurunu elde etti.
Ancak 1917 baharında Ramanujan hastalanacak ve sonrasında da bir türlü tam olarak iyileşemeyecekti. Başta mide ülseri sanılan rahatsızlığının, aslında verem olduğu anlaşıldı. 1919 baharında Ramanujan Hindistan’a döndü. Ancak sağlığı artık oldukça kötüydü. Buna rağmen matematik çalışmalarına devam etti. Ne yazık ki Ramanujan 26 Nisan 1920’de henüz 32 yaşındayken hayatını kaybetti.

Srinivasa Ramanujan’ın Günümüze Mirası
Ramanujan, çoğu zaman teoremlerine kanıt eklemiyordu; bu da onun çalışmalarının başlangıçta anlaşılmasını zorlaştırıyordu. Söz konusu teoremlerden biri, ancak sekiz yıl sonra, 1921’de L. J. Rogers tarafından on sayfalık bir çalışmayla kanıtlandı.
Hardy, bu ve benzeri teoremleri çalışma arkadaşı John Littlewood ile tartıştıktan sonra şu sonuca vardı: “Bu teoremler doğru olmalı; çünkü eğer doğru olmasalardı, kimsenin onları hayal edecek kadar büyük bir zihni olmazdı.” Gerçekten de öyleydi.
100 yılı aşkın bir süre sonra matematikçiler hâlâ Ramanujan’ın ilahi dehasını anlamaya çalışıyorlar. Çünkü onun vizyonları matematik dünyasının en farklı köşelerinde tekrar tekrar karşılarına çıkıyor.
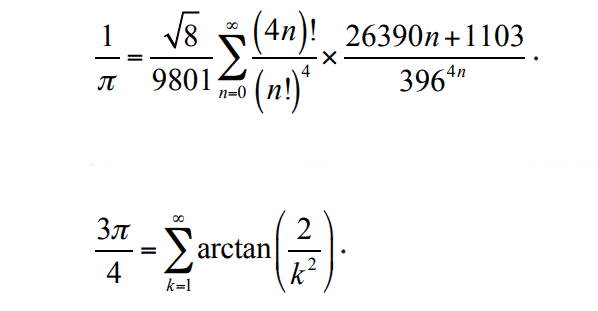
Örneğin, Ramanujan hayattayken kimse kara deliklerin incelenecek bir şey olduğunu bile bilmiyordu. Ancak karadeliklerin özelliklerini açıklamak için kullanılan ilk formüllerden bazılarını Srinivasa Ramanujan farkında olmadan geliştirmişti.
Kendisinin zihninin nasıl çalıştığını daha iyi anlamak için aşağıdaki örneğe göz atın. Günümüzde Pi sayısını hesaplamak için yüzlerce formül vardır. Bu formül de Ramanujan tarafından 1914 yılında yazılmıştır. Formül ile ilgili olan ilginç şey ise gerçekten işe yaradığının 1985 yılında ancak bilgisayarların hayatımıza girmesinin devamında ispatlanmasıdır.
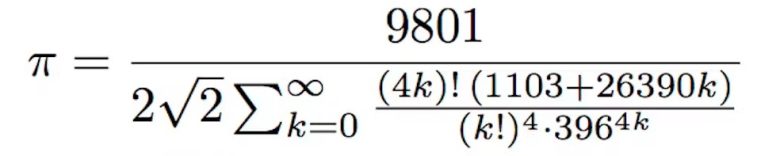
Sonuç olarak
En son olarak, Mourtada’nın cebirsel denklemlerle tanımlanan eğriler ve yüzeyler üzerine yaptığı çalışmada Ramanujan denklemleri ortaya çıktılar. Mourtada ve mesai arkadaşları bu bağlantıyı daha iyi anlamak için on yıldan fazla zaman harcadılar.
Kaynaklar ve ileri okumalar:
- Ramanujan: Dream of the possible; Kaynak site: Plus Maths. Yayınlanma tarihi: 20 Nisan 2018. Bağlantı: Ramanujan: Dream of the possible
- Math Is Still Catching Up to the Mysterious Genius of Srinivasa Ramanujan. Yayınlanma tarihi: 21 Ekim 2024. Kayak site: Quanta magazine. Bağlantı: Math Is Still Catching Up to the Mysterious Genius of Srinivasa Ramanujan
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






Gayret, sabır,,,,,,,,tabi en önemlisi sağlık hele hele ruh sağlığının önemini anlatabilmek ne mümkün.