Matematikte bazı varsayımlar anlaşılması kolay ancak kanıtlanması son derece zor olanlar kategorisine girer. Buna bir örnek asal sayıların sayı doğrusu üzerine dağılımı ve ikiz asal sayılar ile ilgilidir.

Asal sayılar, sayı teorisinin temel yapı taşlarıdır. Çünkü her tam sayı, yalnızca tek bir biçimde asal sayıların çarpımı olarak ifade edilebilir. Matematikçiler, asal sayıların sonsuz sayıda olduğunu 2.000 yıldan uzun süre önce Öklid’in yaptığı ispatla öğrenmişlerdi. Ancak asal sayıların sayılar arasında nasıl dağıldığını anlamaya çalışmak, yüzyıllardır süren bir zorluk olmaya devam ediyor.
Sayı doğrusu üzerinde ilerledikçe asal sayılar seyrekleşir. Buna rağmen, belirli aralıklarla kümelenme eğiliminde oldukları da gözlemlenir. Bazen birbirine çok yakın asal sayılarla karşılaşılır, bazen de uzun süre hiç asal sayı gelmez. Bu düzensiz ama yine de bazı kalıplar taşıyan dağılım, asal sayılarla ilgili en temel gizemlerden biridir.

Örneğin, ilk 10 sayıya baktığımızda 2, 3, 5 ve 7’nin asal olduğunu görürüz. Yani bu aralıktaki sayıların yüzde 40’ı asaldır. Ancak sayı aralığı büyüdükçe bu oran hızla düşer. İlk 100 sayı içinde sadece 25 tane asal sayı olur. 1001 ile 1100 arasındaysa bu sayı 16’ya iner. 100001 ile 100100 arasındaki asal sayı sayısı ise yalnızca 6’dır.
Tüm 10 basamaklı sayıları düşündüğümüzde, bunların yaklaşık sadece yüzde 4’ü asaldır. Bu örnekler, asal sayıların sayı doğrusu üzerinde giderek seyrekleştiğini açıkça gösterir.
İkiz Asallar Varsayımı Nedir?
İkiz asal sayılar varsayımı, sayı teorisinin en dikkat çekici problemlerinden biridir. Söylemesi kolay, ancak kanıtlaması son derece zordur. Bu varsayım, farkı yalnızca 2 olan asal sayı çiftlerinin sonsuz sayıda olduğunu öne sürer. Örneğin (3, 5), (11, 13) ve (29, 31) bu tür çiftlere örnektir.
Matematikçiler, 18. yüzyıldan beri asal sayıların küçük sayılar arasında daha sık, büyük sayılara doğru ise giderek daha seyrek bulunduğunu biliyor. İkiz asal sayılar ise normal asal sayılardan bile daha enderdir. Bu nedenle yeni ikiz asal çiftleri bulmak her zaman kolay olmamıştır.
İlke olarak, bir asal sayıyla ondan sonraki asal sayı arasındaki ortalama mesafe, ln(p) yani p sayısının doğal logaritması kadardır. Örneğin küçük bir sayı olan p = 19 için bu değer yaklaşık ln(19) ≈ 3 olur. Daha büyük bir asal sayı olan 2.147.483.647 için ortalama mesafe yaklaşık 22‘dir. Bu örneklerin gösterdiği gibi, asal sayılar arasındaki ortalama mesafe, sayı büyüdükçe artar.
Bu durumu şöyle hayal edebilirsiniz. Bir asal sayı olan p noktasında durduğunuzu varsayalım. Asal Sayı Teoremi’ne göre, bir sonraki asal sayıya ulaşmak için ortalama olarak lnp (p’nin doğal logaritması kadar) adım atmanız beklenir. Ancak bu sadece ortalamadır. Bazen daha kısa mesafelerde asal sayılarla karşılaşırsınız, bazen de çok daha uzun süre yürümek gerekir.
İşte bu durum, asal sayı çiftlerinden oluşan ve aralarında yalnızca 2 fark bulunan ikiz asalları sayı teorisyenleri için bu kadar ilgi çekici kılar. Ortalama mesafe büyüdükçe, bir noktadan sonra artık hiç ikiz asal kalmamış olabilir. Ancak sayı doğrusu üzerinde bir noktadan sonra neden birdenbire hiç ikiz asal çıkmasın? Sayı teorisyenleri, ikiz asal çiftleri giderek seyrekleşse de, ne kadar ileriye giderseniz gidin eninde sonunda yeni bir ikiz asal çiftiyle karşılaşacağınızı varsayar.
Bilgisayar destekli hesaplamalar da bu düşünceyi destekliyor. Bugüne kadar bulunan en büyük ikiz asal çifti şu şekilde: 2.996.863.034.895 × 21.290.000 + 1 ve 2.996.863.034.895 × 21.290.000 – 1.
Bu iki sayı da 388.342 basamak uzunluğunda. Yine de, bilgisayarlar bu çiftlerin sonsuz sayıda olduğunu hiçbir zaman ispatlayamaz. Bunun için çok daha güçlü yöntemler gerekiyor.
Ne Kadar İlerleme Kaydettik?
2013 yılında, daha önce neredeyse hiç tanınmayan bir matematikçi tam da bu yönde büyük bir adım attı. Yitang Zhang, sayı teorisi uzmanları dışında pek bilinmeyen bir isimdi. Ancak yayımladığı bir makaleyle tüm matematik dünyasında büyük bir etki yarattı. İkiz asal sayılar varsayımını doğrudan kanıtlayamadı, fakat ona çok yakın bir sonuç elde etti—ve bu, 19. yüzyıldan beri bu alanda atılmış en büyük adımdı.
Zhang, aralarındaki fark 70 milyondan küçük olan asal sayı çiftlerinin sonsuz sayıda olduğunu gösterdi. Eğer bunu 2 farkı için kanıtlayabilseydi, ikiz asal sayılar varsayımı da doğrudan ispatlanmış olacaktı. Ancak onun ortaya koyduğu sonuç, bu geniş aralık içinde mutlaka en az bir asal sayı çifti biçiminde (p, p + N) örüntüsünün sonsuz kez tekrarlandığını gösterdi.
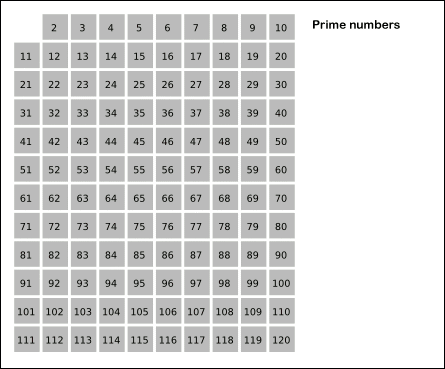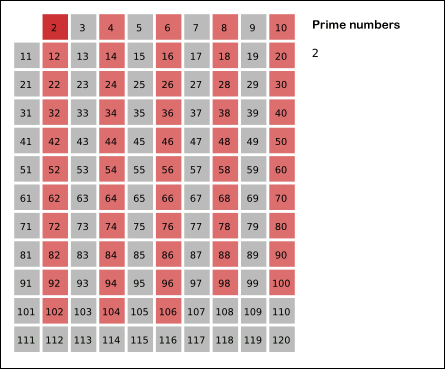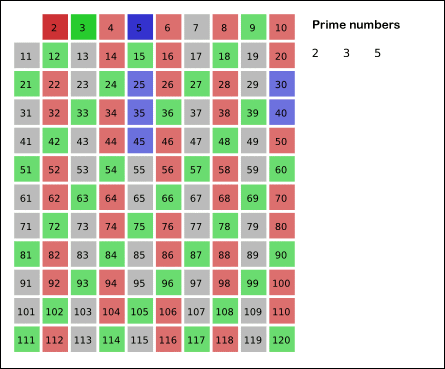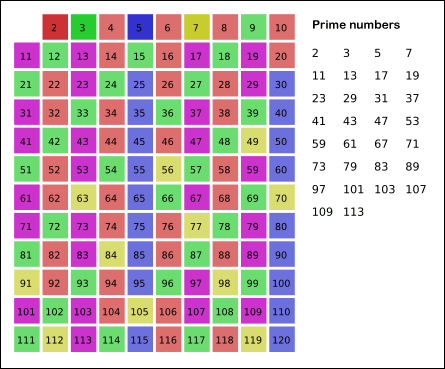
Zhang bu sonuca, matematikçilerin asal sayı eleği dediği bir yöntemle ulaştı. Bu yöntem, adını Antik Yunanlı matematikçi Eratosthenes’ten alır. İlk olarak çift sayılar (2 hariç), ardından 3’ün, 5’in, 7’nin katları elenir. Geriye sadece asal sayılar kalır. Zhang, bu temel fikri modern tekniklerle geliştirerek bugüne kadar ulaşılamayan bir sonuca ulaşmayı başardı.
Bunun üzerine dünya genelinden matematikçiler Zhang’ın yöntemini geliştirerek bu farkı küçültmeye çalıştı. Ortak bir proje ile bu fark, 70 milyondan 4.680’e indi. Aynı dönemde, iki Fields Madalyalı matematikçi — Terence Tao ve James Maynard — bu yöntemi bağımsız olarak yeniden düzenlediler. Geliştirdikleri yeni eleyici yöntemle bu fark N=246 değerine kadar düştü. Bu rekor hâlâ kırılmadı.
Sonuç Olarak
Bu şu anlama gelir: Farkı 2 ile 246 arasında olan asal sayı çiftlerine bakarsak, bu aralıktaki en az bir fark değeri için bu çiftler sonsuz sayıda vardır. Ama hâlâ farkın kesin olarak 2 olduğu, yani gerçek ikiz asal çiftlerinin sonsuz sayıda olduğu kanıtlanamadı. Yine de bu gelişmeler, çok uzun süre ilerleme sağlanamayan bir alanda önemli bir dönüm noktası oldu.
Kaynaklar ve ileri Okumalar:
- Mathematical mysteries: twin primes; Yayınlanma tarihi: 1 Ocak 1998; Kaynak site: Plus Math. Bağlantı: Mathematical mysteries: twin primes/
- Goldston, D. & Graham, Sidney & Pintz, J. & Yilidirm, C.. (2005). Small gaps between primes or almost primes. Transactions of the American Mathematical Society. 361. 10.1090/S0002-9947-09-04788-6.
- Wong, Bertrand. (2021). The Twin Primes. 40E. 75-86. 10.5958/2320-3226.2021.00008.4.
- How Can Infinitely Many Primes Be Infinitely Far Apart? Yayınlanma tarihi: 21 Temmuz 2022. Kaynak site: Quanta Magazine. Bağlantı: How Can Infinitely Many Primes Be Infinitely Far Apart?
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel