Eğer mirasınızı birkaç kelime ya da sembolle ifade etmeniz gerekseydi, neyi seçerdiniz? Johann Carl Friedrich Gauss (1777–1855) için bu sorunun yanıtı son derece açıktı. Geride sayısız matematiksel başarı bırakmış olmasına rağmen, mezar taşına kazınmasını özellikle istediği şey yalnızca bir şekildi: düzgün bir heptadekagon—yani 17 kenarlı simetrik bir çokgen.

Gauss, 18 yaşındayken, yalnızca cetvel ve pergel kullanarak düzgün bir 17-genin çizilebileceğini kanıtlamıştı. Bu, antik çağlardan beri çözülmemiş ve Yunan matematikçilerin dahi başa çıkamadığı bir problemi çözdüğü anlamına geliyordu. Gauss, bu sonucu yaşamı boyunca gerçekleştirdiği en önemli katkılardan biri olarak değerlendirdi.
Antik Yunanlılar geometri ustaları idi ve özellikle bir pergel ve cetvelle oluşturulan yapılara özel bir önem vermişlerdi. Ancak o dönemde kullanılan her iki aletin üzerinde herhangi bir işaret yoktu. Yani cetvel bir uzunluğu ölçmeye değil yalnızca düz bir çizgi çizmeye yarıyordu. Benzer biçimde bir pergel ile de yapabileceğiniz tek şey, merkezi verilen ve belli bir yarıçapa sahip çember çizmekti.

O dönemin matematikçilerinin amacı elbette matematiği zorlaştırmak değildi. Aslında bir geleneği devam ettirmeye çalışıyorlardı. Çünkü pergel ve cetvelle şekiller oluşturma oyunu, Öklid’in Elemanlar kitabında yer alıyordu.
Neden Matematikçiler Belli Geometrik Şekilleri Çizmek İçin Uğraştılar?
Öklid, bir şeklin ya da geometrik bir nesnenin yalnızca var olduğunu kabul etmekle yetinmiyordu. Onları, en basit öğeler olan doğrular ve çemberler kullanarak açıkça inşa etmeyi amaçlıyordu. Hedefi, tüm geometriyi mümkün olan en az sayıdaki varsayımdan yola çıkarak yapılandırmaktı.
Üçgen çizmek oldukça kolaydır. Tek yapmanız gereken, sayfaya üç rastgele nokta yerleştirip bu noktaları doğrularla birleştirmektir. Ancak, mükemmel simetriye sahip şekiller çizmek istediğinizde işler değişir.
Düzgün çokgenler, en yüksek simetriye sahip geometrik şekillerdir. Tüm kenarları eşit uzunluktadır ve iç açılarının ölçüleri birbirine eşittir. Kareler ve eşkenar üçgenler bu tanıma uyarken, dikdörtgenler ve eşkenar dörtgenler düzgün çokgen sayılmaz.
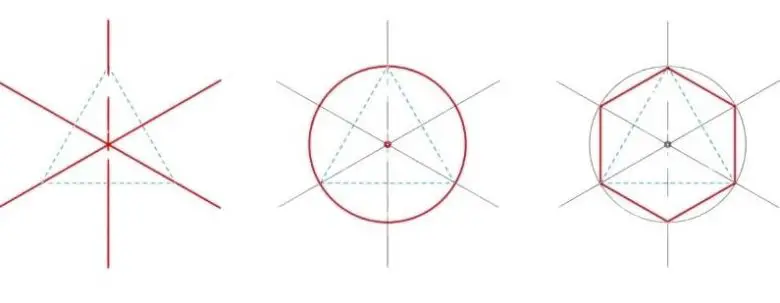
Öklid, üç, dört ve beş kenarlı düzgün çokgenleri pergel ve cetvelle nasıl çizebileceğimizi gösterdi. Bu temel örneklerden yola çıkarak, bir düzgün çokgenden hareketle kenar sayısını iki katına çıkaran basit işlemler geliştirdi. Bu sayede daha karmaşık çokgenlerin inşasını mümkün kıldı.
Böylece üç, dört ve beş kenarlı düzgün çokgenleri sırasıyla altı, sekiz ve on kenarlı şekillere; ardından 12, 16, 20 kenarlı ve daha fazlasına dönüştürmek olası oldu. Öklid ayrıca, üç ve beş kenarlı düzgün çokgenleri birleştirerek düzgün 15-genin de inşa edilebileceğini gösterdi.
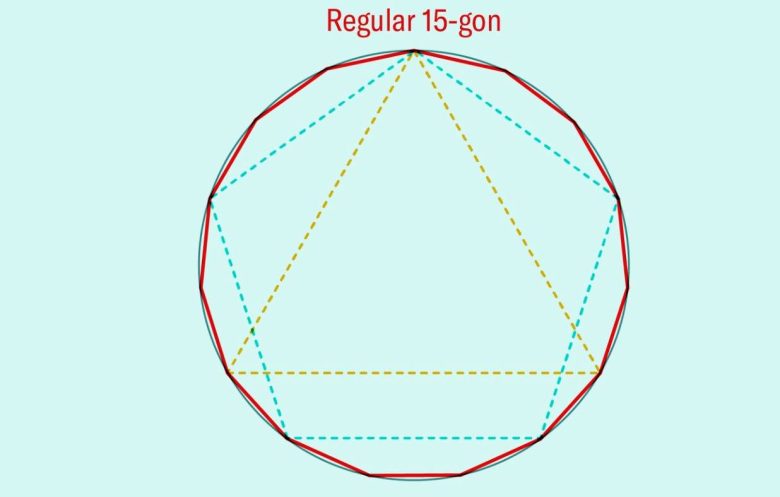
Ancak ilerleme burada durdu. Öklid, kuramsal olarak düzgün bir 3.072-genin (on kez ikiye katlanmış bir üçgen) çizilebileceğini biliyordu. Ancak düzgün bir yedigen ya da on birgenin nasıl çizileceği konusunda hiçbir fikri yoktu.
Bu durumda ortaya şu soru çıktı. “Hangi düzgün çokgenler yalnızca cetvel ve pergel ile çizilir?”. Bu soru, iki bin yıl boyunca cevapsız kalacaktı. Aslında bu kadar uzun süre yanıtlanamaması, matematik dünyası için bir şanstı. Çünkü bu sayede Carl Friedrich Gauss ile tanışacaktı.
Gauss Onyedigen İle İlgili Sorunu Nasıl Çözdü?

(Ressam: Christian Albrecht Jensen, 1840)
1795 sabahında, henüz 18 yaşında olan Gauss yataktan kalktı. O gün, düzgün bir onyedigenin nasıl çizileceğini keşfetmişti. Bu önemli bulgusunu hemen günlüğüne not etti. Aynı gün, profesyonel matematikçi olma kararını da kesinleştirdi.
Üstelik bu sonuca herhangi bir çizim yapmaksızın tamamen zihinsel olarak ulaştı. Çünkü kendisi, düzgün çokgen çizme sorununu, belirli uzunlukta bir doğru parçası üretme problemine indirgemeyi başarmıştı.
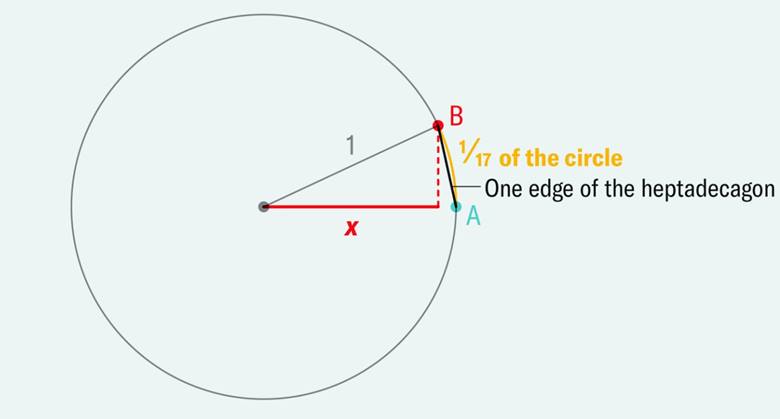
Bir 17-gen çizmek için, yarıçapı 1 olan bir birim çember çizdiğimizi ve A noktasını başlangıç olarak aldığımızı düşünelim. Çemberin çevresi boyunca tam 17’de 1 oranında ilerleyerek, A noktasının yukarısına denk gelen kırmızı bir B noktasını hayal edelim.
Eğer bu kırmızı noktayı, mavi A noktasından yalnızca cetvel ve pergel kullanarak oluşturabilirsek, aynı işlemi çember üzerinde 17 kez tekrarlayarak tüm köşeleri birleştirir ve düzgün bir heptadekagon çizebiliriz. Matematiksel olarak merak edenler için, bu uzunluk şu ifadeye eşittir: x = cos(2π⁄17)
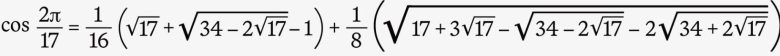
Gauss, x=cos(2π/17) uzunluğunu yalnızca cetvel ve pergelin izin verdiği beş temel cebirsel işlemle ifade etmeyi başardı. Böylece, teorik olarak bu şekli çizmenin mümkün olduğunu gösterdi.
Sonuç olarak
Daha da etkileyici olan, Gauss’un hangi düzgün çokgenlerin cetvel ve pergel ile çizilebileceğini, hangilerinin çizilemeyeceğini tamamen belirlemiş olmasıdır. Kesin kanıt, 1837 yılında Pierre Wantzel tarafından ortaya konmuş olsa da, temel yapıyı ilk olarak Gauss kurmuştur.
Gauss yalnızca hangi düzgün çokgenlerin çizilebileceğini tarif etmekle kalmadı. Wantzel ile birlikte, Öklid’in yüzyıllar önce yaşadığı hayal kırıklığını da bilimsel bir temele oturttu. İkili, düzgün yedigenin (7 kenarlı) ve on birgenin (11 kenarlı) yalnızca cetvel ve pergel kullanılarak çizilemeyeceğini matematiksel olarak kanıtladı. Aynı şekilde, sonsuz sayıda başka düzgün çokgenin de bu araçlarla inşa edilmesi mümkün değildir. Böylece antik geometrinin sınırları, modern cebirin araçlarıyla kesin biçimde çizilmiş oldu.
Biyografi yazarı G. Waldo Dunnington’a göre, Gauss binlerce yıllık bu problemi çözdüğü için büyük bir gurur duyuyordu. Bu nedenle bir arkadaşına, mezar taşına düzgün bir heptadekagon kazınmasını istediğini söylemişti. Ne yazık ki bu dileği gerçekleşmedi. Ancak Gauss’un doğum yeri olan Almanya’nın Braunschweig (Brunswick) kentindeki bir anıtta, arka yüzüne 17 köşeli bir yıldız işlenmiştir.
Kaynaklar ve ileri okumalar
- Why This Great Mathematician Wanted a Heptadecagon on His Tombstone. Yayınlanma tarihi: 12 Eylül 2024. Kaynak site: Bağlantı: Why This Great Mathematician Wanted a Heptadecagon on His Tombstone
- Why are Most Polygons Impossible to Construct? Kaynak site: Youtube. Bağlantı: Why are Most Polygons Impossible to Construct?
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel