Eliptik eğri kriptografisi, Bitcoin ve diğer kripto paraların dayandığı güvenlik sistemidir; aynı zamanda başka internet platformlarında da hızla yayılan bir şifreleme yöntemi hâline gelmiştir. Peki Rönesans sanatı, modern kriptografiyi yöneten matematiğe nasıl yol açtı?

Filippo Brunelleschi’den Bitcoin’e uzanan yolun ilk adımları, perspektif kuralları içindeki görsel geometrinin, okulda öğrendiğimiz düzenli noktalar ve doğrular dünyası olan Öklid geometrisiyle ilişkilendirilmesiyle atıldı. Bu yönde ilk katkıyı, 17. yüzyılda perspektif geometrisi üzerine çalışan Fransız matematikçi Girard Desargues yaptı.
Ancak Desargues, fikirlerini anlaşılması güç ve ağır bir dille kaleme aldığı için çağdaşlarının ilgisini çekemedi. Temel katkıları, kendi dönemi için bile son derece küçük sayılan, yalnızca 50 baskılık bir kitapta yer aldı.

Desargues hayattayken, çalışmalarının gerçek anlamda tek sıkı takipçisi yine bir Fransız matematikçi olan Blaise Pascal oldu. Pascal, daha sonra “projektif geometri” adını alacak olan bu alanın gelişimine kendi teoremini ekledi.
Desargues’ın eserleri uzun süre göz ardı edilmiş olsa da, onun yaptığı atılım devrim niteliğindeydi. Öklid geometrisine, “sonsuzdaki noktalar” ve “sonsuzdaki doğrular” kavramlarını eklemişti.
Desargues’ın kurduğu sistemde, her doğru çifti tam olarak bir noktada kesişir; paralel doğrular için özel bir durum yoktur. Ayrıca parabol ve hiperbol gibi eğriler de, sırasıyla bir ya da iki “sonsuz nokta” eklendiğinde, elipslerle aynı çerçeve içinde ele alınabilir. Böylece farklı eğriler arasında biçimsel bir birlik sağlanır.
Bu fikirler son derece değerli olmasına rağmen, yüz yılı aşkın bir süre boyunca neredeyse tamamen göz ardı edilecekti. İlerleyen süreçte, Fransız matematikçi olan Gaspard Monge, benzer sorular üzerinde çalışmaya başladı ve benzer sonuçlara, Desargues’tan bağımsız olarak ulaştı. 19. yüzyılda projektif geometriyi sistemli bir kuram hâline getiren isim ise Jean-Victor Poncelet’tir.

Eğriler ve İntegraller
Poncelet projektif geometri üzerine kitabını tamamlarken, aynı yıllarda Norveçli matematikçi Niels Henrik Abel eliptik integraller üzerinde çalışıyordu. Matematikçiler bu zor ifadeleri başlangıçta bir elipsin çevresini hesaplamak için geliştirmişti.
Abel, bazı durumlarda bu integrallerle doğrudan uğraşmak yerine, onların terslerini kullanmanın mümkün olduğunu fark etti. Bugün eliptik eğriler dediğimiz bu nesnelerle çalışmak çok daha kolaydı. Eliptik eğrilerin ayrıntılı kuramını geliştirmek ise başkalarına kaldı. Abel, bu konudaki makalesini yayımladıktan birkaç ay sonra, henüz 26 yaşındayken veremden yaşamını yitirdi.
Fransız matematikçiler projektif geometri ile Öklid geometrisini birleştirmeyi başarmıştı. Ancak projektif geometriyi, cebir öğrencilerinin denklemleri çizmek için kullandığı Kartezyen koordinat sistemiyle kaynaştırmak Alman matematikçi August Möbius’a düştü.
Möbius, bugün “homojen koordinatlar” olarak bilinen bir yöntem geliştirdi. Bu koordinat sistemi, eliptik eğri kriptografisinin matematiksel altyapısında kilit bir rol oynar.
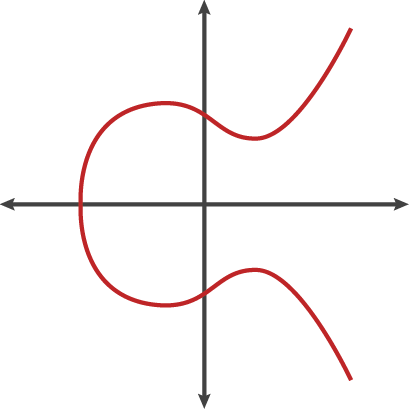
1901 yılında Fransız matematikçi Henri Poincaré, eliptik bir eğrinin grafiği üzerindeki rasyonel koordinatlı noktaların özel bir yapı oluşturduğunu fark etti. Poincaré, eğri üzerindeki iki rasyonel noktayı alıp üçüncü bir nokta üreten bir işlem tanımladığınızda elde edilen sonucun her zaman yine eğri üzerindeki rasyonel bir nokta olduğunu gösterdi.
Daha da önemlisi, bu eliptik eğri gruplarının Abelyen olduğu ortaya çıktı. Yani noktaları hangi sırayla topladığınızın sonucu etkilemiyordu. Bu matematiksel temeli, 1980’lerin ortasında, IBM’den Victor S. Miller ve Washington Üniversitesi’nden Neal Koblitz kriptografi alanına taşıdı.
Her ikisi de birbirinden bağımsız olarak, eliptik eğri gruplarına dayalı açık anahtarlı bir şifreleme sistemi kurulabileceğini keşfetti. Bu buluş, bugün eliptik eğri kriptografisi olarak bildiğimiz yöntemin doğrudan başlangıcı oldu.
Şifreleme Anahtarları
Bugün internetteki güvenli iletişimin neredeyse tamamı açık–özel anahtar şifrelemesine dayanır. Bu yöntemde iki anahtar vardır.. Kullanıcı, özel anahtarı yalnızca kendisi saklar ve kimseyle paylaşmaz. Sistem, bu özel anahtardan bir açık anahtar üretir ve kullanıcı bu anahtarı herkese açık biçimde gönderir. Mesajı açmak için açık anahtar ile ona karşılık gelen özel anahtar birlikte gerekir.
Eliptik eğri kriptografisi bu sistemi eliptik eğriler üzerindeki matematikle kurar. İletişim kuracak taraflar önce aynı eliptik eğriyi ve aynı başlangıç noktasını seçer. Ardından her taraf, bu noktadan başlayarak yalnızca kendisinin bildiği rastgele sayıda toplama işlemi yapar. Her biri ulaştığı son noktaya karşılık gelen sayıyı karşı tarafa gönderir. Bu sayılar açık anahtarları oluşturur.
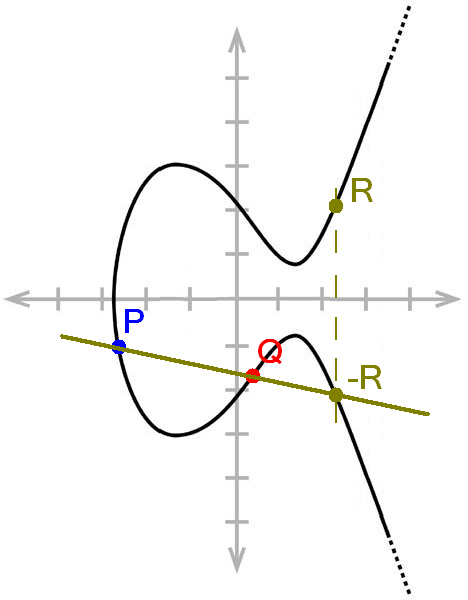
Sonraki aşamada her taraf, karşısından aldığı açık anahtar üzerinde, başlangıçta yaptığı toplama işlemlerinin aynısını uygular. Ortaya çıkan bu ortak sayı, veriyi şifrelemek ve çözmek için kullanılır.
Eliptik eğri kriptografisi şifreleme dünyasına görece geç girdi. Araştırmacılar ilk pratik araçları 2004 yılında geliştirdi. Bu nedenle yöntem, Web’in erken dönem standartları arasına giremedi. Buna karşılık, 2009’da ortaya çıkan Bitcoin eliptik eğri kriptografisini temel alarak bu yöntemin yaygınlaşmasını sağladı.
Sonuç olarak

Kripto paraların fiilî standardı hâline gelmesi, eliptik eğri kriptografisini daha tanınır kıldı. Buna rağmen, standart yöntem olan RSA şifrelemesinin hâlâ oldukça gerisindedir. Yine de eliptik eğri kriptografisinin RSA’ya göre önemli üstünlükleri vardır. Bit başına daha yüksek güvenlik sağlar ve daha hızlı çalışır. Ayrıca yaygın olarak kullanılan 2.048 bitlik RSA anahtarlarından belirgin biçimde daha güvenlidir.
Daha kısa anahtarlar, web sayfalarının daha hızlı yüklenmesini sağlar ve sunucu tarafındaki işlemci yükünü azaltır. Ayrıca eliptik eğri kriptografisinin ilkeleri, kuantum bilgisayarlara karşı daha dayanıklı şifreleme sistemleri geliştirme çalışmalarında da kullanılmaktadır.
Kaynaklar ve ileri okumalar
- Yan, Yuhan. (2022). The Overview of Elliptic Curve Cryptography (ECC). Journal of Physics: Conference Series. 2386. 012019. 10.1088/1742-6596/2386/1/012019.
- This Cutting-Edge Encryption Originates in Renaissance Art and Math. Yayınlanma tarihi: 28 Mayıs 2025. Kaynak site: Scientific American. Bağlantı: This Cutting-Edge Encryption Originates in Renaissance Art and Math
Matematiksel