Mantık, mekanik bir akıl yürütme sistemidir. Kararların ve sonuçların bir sembolik bir dizi ifadeden türetildiği veya çıkarıldığı bir kurallar dizisidir. Bu sayede sorularımızın cevaplarına evet ya da hayır biçiminde ulaşmamız mümkündür.
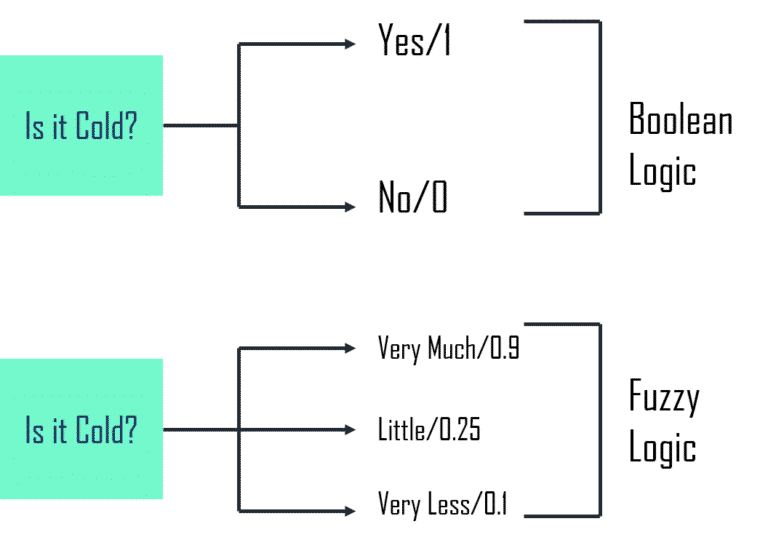
Ancak gerçek hayatta karşılaştığımız her sorunun cevabı bu kadar net olmayacaktır. Hayatta belki, birazcık çok, birazcık az, bir bakıma iyi ama çok iyi değil gibi verdiğimiz cevaplar da vardır. Bu gibi cevapları ikili sistemle yani 0 veya 1 ile göstermek tahmin ettiğiniz gibi mümkün değildir. Bu durumda yardımımıza bulanık mantık ( Fuzzy Logic) yetişecektir.
Herhangi bir bilgisayara geçerli girdiler verdiğimiz zaman bilgisayarımız bize uygun çıktılar sağlayacaktır. Bununla birlikte, bilgisayarlar da belirsizlik ile baş etme konusunda başarılı sayılmazlar. Ancak bulanık mantık tarafından kontrol edilen bir sistem, karmaşık fenomenlerin daha iyi analiz edilmesine izin verir.

Daha iyi anlaşılabilmesi için bir örnek verelim. Evimizdeki çamaşır makinesini düşünelim. Standart bir çamaşır makinesi, içindeki çamaşırın ne kadar kirli olduğuna bakmasızın yıkama işlemini daha önce programlandığı gibi sabit bir şekilde yapar.
Öte yandan akıllı bir çamaşır makinesiyse, yıkama suyunu inceleyerek çamaşırların temizlenme durumuna bakar. Makine, “Eğer çamaşır çok kirliyse daha uzun yıka, az çamaşır varsa az su kullan” gibi önerme cümlelerine göre kontrol yapar. Elde ettiği sonuçlara göre yıkama programını değiştirir. Bu bulanık mantık sonucunda mümkün olacaktır.
1920’li yıllarda felsefeci Jan Lukasiewicz, ikiden fazla değer içeren ifadelerin kullanılabildiği mantığın başlangıcını oluşturdu. Daha sonra 1965’te Lotfi Zadeh, Lukasiewicz’in mantığının doğruluk derecelerini tanımladı..
“Bulanık Kümeler” başlıklı makalesinde Zadeh, bilgi işlemede kullanılan veri türünü yansıtmaya çalışmış ve bu tür kümeler için temel mantıksal kuralları türetmiştir. Standart küme teorisi, bir elemanın bir kümeye ait olup olmamasına izin verir. Bulanık küme kuramı ise sınırların kesin olmadığı durumları da göz önünde bulundurur.
Bulanık Mantık Nasıl Çalışır?
Boolea mantığı doğru ve yanlış biçiminde iki değer üzerine kuruludur. Ancak bulanık mantık bir önerme için bir dizi doğruluk değerine izin verir. Bulanık doğruluk değerleri ayrıca bulanık mantıksal operatörler gerektirir. Örneğin, Boole cebrinin AND operatörünün bulanık versiyonu, iki girişin minimumunu veren MIN operatörüdür.
Bulanık mantığın çalışma biçimi aslında insanların akıl yürütme sürecine benzer. Bir bulanık değişkenin hangi bulanık kümeye ait olduğuna karar vermenin matematiksel bir sürecine dayanır. Bulanık mantığın esnekliği, bu kümelerin bulanık sınırlarından gelir. Hemen bir örnek verelim.
Geleneksel bir fırın tam sıcaklık esasına göre çalışır. Fırın seçilen herhangi bir sıcaklığa ulaştığında fırında bulunan bir termometre fırın ısıtıcısına giden gücü keser, sıcaklık belli bir diğerinin altına düştüğünde de tekrar harekete geçirir. Bu mantık, fırının içinde ne olursa olsun aynı şekilde gerçekleşir.
Bulanık mantık sıcaklık kontrolüne sahip bir mikrodalga fırında ise sonuç kesin sıcaklıklara bağlı değildir. Bunun yerine süreç şuna benzer: “EĞER (süreç çok soğuk) VE (süreç soğuyor) ise SONRA (daha fazla ısı ekle) ”veya” EĞER ( süreç çok sıcak) VE (süreç soğuyor) ise SONRA (şimdi ısıt). “gibidir.
Bulanık Mantık Neden Gereklidir?
Bulanık mantık artık bilgisayar kontrollü sistemlerin her yerde bulunan bir parçasıdır. Hava tahmininden hisse senedi alım satımına kadar birçok uygulamaya sahiptir ve yapay zeka sistemlerinin programlanmasında hayati bir rol oynar. IBM’in Watson’ı, bulanık mantık kullanan en iyi bilinen yapay zeka sistemlerinden biridir.
Bulanık mantığı cazip kılan bazı özellikleri vardır. Öncelikle insan düşünce sistemi sayısal değil sözel bilgileri işlemeye odaklıdır. İfade etmeye çalıştığı şeyler için dilsel değerleri kullanır. Bulanık mantık da benzer şekilde çalıştığı için, insan mantığına yaklaşık sonuçlar üretir.
Ayrıca bazen problemleri çözmek için gerekli verilere ulaşmak zor veya maliyetlidir. Elimizde yeterli bilgilerin bulunmadığı bu durumlarda bulanık mantık kesin olmayan durumlarda bile makul sonuçlar verecektir.
Bulanık mantık, insanların karar verme sürecini taklit ettiğinden, en çok belirsiz veya çarpık girdilerle karmaşık problemleri modellemek için kullanışlıdır. Doğal dil ile benzerlikleri nedeniyle, bulanık mantık algoritmalarının kodlanması standart mantıksal programlamaya göre daha kolaydır ve daha az talimat gerektirir. Böylece bellek depolama gereksinimlerinden tasarruf sağlar.
Bu avantajlar, bulanık mantığın kesin olmayan doğasından dolayı dezavantajlarla birlikte gelir. Sistemler hatalı veri ve girdiler için tasarlandığından, hatalı sonuçları önlemek için test edilmeli ve doğrulanmalıdır. Ayrıca, bulanık kontrol sistemleri, insanların uzmanlığına ve bilgisine bağlıdır.
Kaynaklar ve ileri okumalar:
- Fuzzy pizza; Yayınlanma tarihi: 17 Ekim 2002; Bağlantı: Fuzzy pizza;
- Fuzzy Logic: Definition, Meaning, Examples, and History; Yayınlanma tarihi: 2 Kasım 2021; Bağlantı: Fuzzy Logic: Definition, Meaning, Examples, and History
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel