Bugüne Kadar Çözülmüş En Zor 9 Matematik Problemi

Matematik, çözülen ve hâlâ çözülememiş pek çok problemle doludur. Bu yazıda, şimdiye kadar çözülmüş en zor dokuz problem üzerinde duracağız.

1) Üç Küp Problemi

Douglas Adams’ın bilim kurgu serisi Otostopçunun Galaksi Rehberi‘nde, iki programcı galaksinin en büyük süper bilgisayarına evrendeki her şeyin anlamını bulma görevini verir. Bilgisayar, 7.5 milyon yıl süren bir işlem sonunda cevabı verir: 42. Ancak programcılar, kimsenin bu cevabın hangi soruya ait olduğunu bilmediğini fark eder. Üç küp problemi de tesadüfen 42 sayısı ile ilişkilidir.

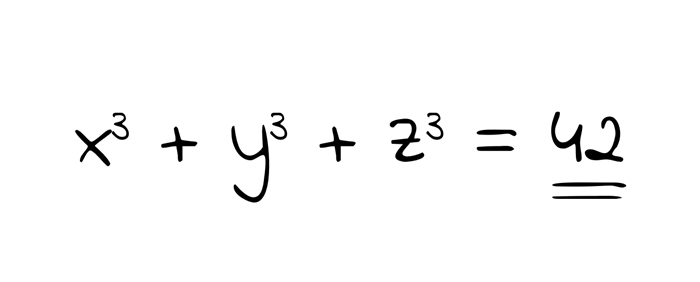
Bu soru en azından 1955’ten beri gündemde. Hatta bazılarına göre, M.S. 3. yüzyılda yaşamış Antik Yunan düşünürleri bile bu problemi tartışmış olabilir. Soru şu: “1 ile 100 arasındaki her sayıyı, üç küp sayının toplamı şeklinde ifade edebilir miyiz?”

Bu aldatıcı derecede basit görünen problem, adını yaklaşık 1800 yıl önce benzer sorular ortaya atan İskenderiyeli matematikçi Diophantos’tan alır ve “Diophantus denklemi” olarak bilinir. Modern matematikçiler, bu probleme yeniden yöneldiklerinde, küçük k değerleri için çözümleri hızlıca buldular. Ancak bazı sayılar inatla çözüm vermedi.

Nihayet 2019 yılında, matematikçi Andrew Booker, 33 sayısı için çözümü buldu. Geliştirdiği bilgisayar algoritmasıyla, x, y ve z değişkenleri için pozitif ve negatif 99 katrilyona kadar olan tüm sayıları tarayarak denklemin çözümünü elde etti. Yine de 42 sayısı için herhangi bir çözüm ortaya koyamadı.

Bir sonraki denemesinde matematikçi Andrew Sutherland’dan yardım aldı. Sutherland, Booker’a Charity Engine adlı küresel bilgisayar ağını kullanma imkânı sağladı. Sonunda Booker ve Sutherland, yaklaşık 1 milyon işlem saati sonunda, k=42 olan Diophantus denkleminin çözümünü bulmayı başardı.

2) Poincaré Sanısı

2000 yılında Clay Matematik Enstitüsü, çözülememiş yedi büyük matematik problemini “Milenyum Problemleri” adıyla duyurdu. Bu problemlerden herhangi birini çözen kişiye 1 milyon dolar ödül verileceğini açıkladı. Bugün, yalnızca Poincaré Sanısı çözüme kavuştu; diğer altı problem hâlâ yanıt bekliyor.

Cebirsel topoloji, 19. yüzyılın sonlarında Henri Poincaré’nin çalışmalarıyla ortaya çıktı. Bu alan, geometri ve topolojideki karmaşık problemleri cebirsel terimlerle ifade ederek, soyut matematiksel yapıları anlamayı mümkün kıldı.

Poincaré, topolojinin temellerini atarken bir soruya odaklandı: Topolojinin en basit üç boyutlu yapısı, dört boyutlu bir yüzeyi tanımlamak için yeterli olabilir miydi? Bu sorgulama, onu matematik tarihinin en ünlü sorularından birine götürdü. Hiçbir belirgin özelliği bulunmayan bir üç boyutlu uzay, mutlaka bir üç boyutlu küre midir? İşte bu soru, Poincaré varsayımının temelini oluşturdu.

Bir yüzyıl sonra Rus matematikçi Grigori Perelman, Poincaré sanısını ispatladı. 2002’de konuyla ilgili 39 sayfalık ilk makalesini alışılmadık bir şekilde internete koydu ve özetini ABD’deki 12 matematikçiye e-postayla gönderdi. Ertesi yıl iki bölüm daha yayımladı. İspatı 2006’da matematik camiası tarafından tamamen kabul edildi.

3) Fermat’ın Son Teoremi

Pierre de Fermat, 17. yüzyılda yaşamış Fransız bir avukat ve matematikçiydi. Onun için matematik, bir hobiden ibaretti. İlginç bir kişiliği vardı ve öldükten sonra, çözümü için matematikçilerin on yıllarını hatta yüzyıllarını harcayacağı ispatsız iddialar bıraktı.

Bu iddialar arasında en zoru, aynı zamanda en meşhuru olan Fermat’nın Son Teoremi’ydi. Bugün “zor matematik problemi” denince akla ilk gelen örneklerden biridir.

Fermat’ın son teoremi, Pisagor teoremine benzer. Ancak Fermat ise, bu denklemdeki üssün 2’den büyük olması durumunda neler olacağını sorguladı. Örneğin x³ + y³ = z³ denkleminin tam sayı çözümleri var mıdır? Peki ya üs 10, 50 ya da 30 milyon olursa ne olur?

Pierre de Fermat cevabın hayır olduğunu iddia etmişti. Bir kitabın kenarına bu teoremi ispatladığını, ancak sayfa kenarında yeterince yer olmadığı için ispatı yazamadığını not etti.

Yüzyıllar boyunca matematikçiler, Fermat’nın gerçekten bir kanıta sahip olup olmadığını merak etti. Bu soru, onun ölümünden tam 330 yıl sonra, 1995’te yanıt buldu. İngiliz matematikçi Sir Andrew Wiles, sonunda bu zor problemi çözdü.

Wiles, teoremi kanıtlamak için matematiğin birçok farklı alanını bir araya getirdi. Bunlardan biri de eliptik eğrilerdi. Ancak bu kavram, Fermat’nın yaşadığı dönemde henüz bilinmiyordu. Bu nedenle, çoğu matematikçi Fermat’nın bu teorem için gerçek bir kanıta sahip olmadığına inanıyor.

4) Sonlu Basit Grupların Sınıflandırılması

Soyut cebir, Rubik Küpü’nü çözmekten, Futurama dizisinde beden değiştirme sahnelerini açıklamaya kadar pek çok alanda karşımıza çıkar. Bu alanın temel kavramlarından biri “grup”tur.

Gruplar sonlu ya da sonsuz olabilir. Belirli bir büyüklükteki (n elemanlı) grupların nasıl göründüğünü anlamak ise n’in değerine göre karmaşıklaşır. Eğer n = 2 ya da 3 ise yalnızca bir tür grup vardır. Ancak n = 4 olduğunda iki olasılık ortaya çıkar. Doğal olarak, matematikçiler herhangi bir n için tüm olası grupların tam listesini çıkarmak istediler.

Bu listeyi kesin biçimde tamamlamak onlarca yıl sürdü; çünkü gerçekten tam olduğunu kanıtlamak son derece zordu. Sonsuz sayıda grup biçimini tanımlamak bir şeydir, ancak listenin tümünü kapsadığından emin olmak bambaşka bir iştir.

20. yüzyılın en büyük matematiksel projelerinden biri sayılan Sonlu Basit Grupların Sınıflandırması çalışması, Harvard’lı matematikçi Daniel Gorenstein tarafından yürütüldü. Gorenstein, 1972’de bu olağanüstü karmaşık planı ortaya koydu.

1985’e gelindiğinde çalışma neredeyse tamamlanmıştı, ancak o kadar çok sayfa ve yayına dağılmıştı ki, tek bir kişinin gözden geçirmesi imkânsızdı. Yıllar içinde, kanıtın farklı bölümleri teker teker incelendi ve sınıflandırmanın gerçekten eksiksiz olduğu doğrulandı.

1990’larda bu dev kanıt matematik camiasında genel kabul gördü. Ardından, bu muazzam yapının daha sade ve anlaşılır biçimde yeniden düzenlenmesi için çalışmalar başladı. Bu sadeleştirme süreci hâlâ devam ediyor.

5) Dört Renk Teoremi

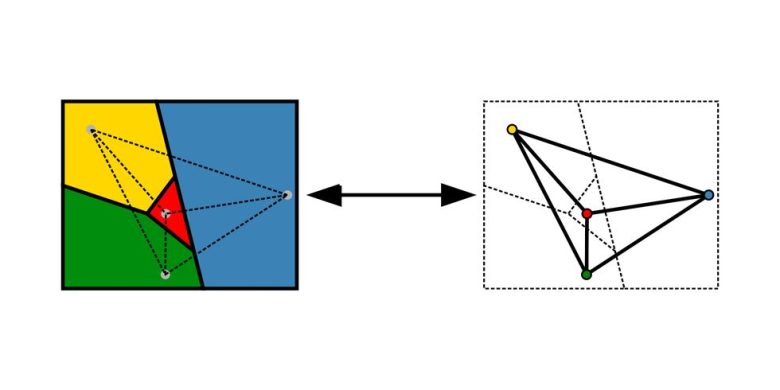
Bu teorem hem söylenmesi kolay hem de kanıtlanması son derece zor olan bir gerçeği anlatır. Bir harita ve dört renkli kalem alın. Kural basittir: Komşu ülkeler ya da eyaletler aynı renge boyanamaz.

Herhangi bir haritayı beş renkle boyamanın olası olduğu, yani Beş Renk Teoremi, 19. yüzyılda kanıtlandı. Ancak bu sayıyı dörde indirmek, yani Dört Renk Teoremini ispatlamak 1976 yılına kadar mümkün olmadı.

Illinois Üniversitesi’nden Kenneth Appel ve Wolfgang Haken, kanıtı sonlu sayıda duruma indirgemeyi başardı. Bilgisayar yardımıyla yaklaşık 2000 olasılığı tek tek kontrol ettiler ve matematik tarihinde eşi görülmemiş bir tür kanıt ortaya koydular.

Başta kanıt tartışmalı olsa da (çünkü kanıtın bir bölümü bilgisayar tarafından doğrulanmıştı) Appel ve Haken’in çalışması sonunda matematikçiler tarafından kabul edildi. Günümüzde bilgisayar destekli kanıtlar oldukça yaygın hale geldi, fakat bu yaklaşımın öncülüğünü Appel ve Haken yaptı.

6) Süreklilik Hipotezi

19. yüzyılın sonlarında Alman matematikçi Georg Cantor, sonsuzluk kavramına bambaşka bir boyut kazandırdı. Cantor, tüm sonsuzlukların aynı büyüklükte olmadığını, yani farklı “kardinaliteler”e (sonsuzluk derecelerine) sahip olduklarını gösterdi. Bugün üniversitelerde ayrık matematik derslerinde öğretilen temel sonuçların çoğu onun çalışmalarına dayanır.

Cantor, reel sayıların kümesinin, doğal sayıların kümesinden daha büyük olduğunu kanıtladı. Bunu |ℝ| > |ℕ| biçiminde yazarız. Doğal sayıların büyüklüğü, yani |ℕ|, “ilk sonsuzluk derecesi”dir; bundan daha küçük bir sonsuz küme yoktur.

Peki reel sayılar bir sonraki, yani “ikinci” sonsuzluk derecesini mi oluşturur? Bu soru, Süreklilik Varsayımı (Continuum Hypothesis, CH) olarak isimlendirilir.

Eğer CH doğruysa, reel sayıların büyüklüğü gerçekten ikinci sonsuzluk derecesidir; ℕ’den büyük ama ℝ’den küçük hiçbir sonsuz küme yoktur. Eğer CH yanlışsa, bu iki küme arasında en az bir ara büyüklük vardır.

Sonuç ne mi oldu? İşte işin ilginç kısmı burada başlar. CH, matematiğin temel aksiyomlarına göre bağımsız bir önermedir. Yani hem doğru olması hem de yanlış olması mümkündür ve hiçbir durumda mantıksal çelişki ortaya çıkmaz. Bu tür bağımsız ifadeler modern matematikte nadir değildir. Örneğin Seçim Aksiyomu da aynı şekilde bağımsızdır.

Çözülmüş En Zor Matematik Problemi İle Tanışalım

Süreklilik hipotezinin bu konuma ulaşması onlarca yıl sürdü ve iki aşamalı bir kanıtla gerçekleşti: ilki tutarlı olduğunu, ikincisi ise tersinin de tutarlı olduğunu gösterdi.

İlk aşama, Avusturya-Macaristan kökenli büyük mantıkçı Kurt Gödel’e aittir. 1938’de hipotezin temel matematik aksiyomlarıyla çelişmediğini gösterdi.

İkinci aşama, yaklaşık yirmi yıl sonra Stanford Üniversitesi’nden Paul Cohen tarafından tamamlandı. Cohen, Forcing adı verilen yeni bir kanıtlama yöntemi geliştirerek CH’nin tersinin de tutarlı olduğunu kanıtladı. Gödel ve Cohen’in çalışmaları, küme teorisinin yüksek lisans düzeyinde bile oldukça zorlayıcı konularıdır.

7) Gödel’in Eksiklik Teoremi

Matematik, uzun süre boyunca mutlak kesinliğin alanı olarak görüldü. Ancak Kurt Gödel, Eksiklik Teoremleri ile bunun bir yanılsama olduğunu gösterdi.

1931 yılında Avusturyalı mantıkçı Kurt Gödel, tarihin en çarpıcı entelektüel başarılarından birine imza attı. O dönemin matematikçileri, tüm matematiksel doğruların üzerine kurulabileceği sağlam bir temel arayışındaydı. Amaç, hem çelişkisiz (tutarlı) hem de eksiksiz olacak bir aksiyomlar sistemi kurmaktı.

Böylece tüm matematiksel gerçekler bu temel ilkelerden türetilebilecekti. Gödel’in yalnızca yirmi beş yaşındayken yayımladığı Eksiklik Teoremleri bu düşünceyi yıktı.

Birinci Eksiklik Teoremi, her matematiksel sistemde kanıtlanamayan ifadelerin var olduğunu söyler. Yani sistem ne kadar güçlü olursa olsun, içinde doğru ama kanıtlanamayan bazı önermeler vardır.

Gödel’in mantığını sade bir şekilde anlamak mümkündür. Şöyle düşünelim: “Bu ifade kanıtlanamaz.” Şimdi olasılıkları inceleyelim. Eğer bu ifade yanlışsa, o zaman “kanıtlanabilir” demektir. Fakat kanıtlanabilirse, söylediği şey —yani kanıtlanamaz olduğu— yanlış olur. Bu bir çelişkidir. Eğer ifade doğruysa, gerçekten kanıtlanamaz demektir. O hâlde ifade doğru ama kanıtlanamaz olur.

Sonuçta elimizde doğruluğu tartışmasız ama kanıtı olmayan bir ifade kalır. Bu durum, Gödel’in Birinci Eksiklik Teoremi’nin özünü gösterir.

Gödel’in ikinci eksiklik teoremi ise bir başka ilginç sonucu ortaya koyar. Bu teorem, herhangi bir tutarlı matematiksel sistemin kendi tutarlılığını kanıtlayamayacağını söyler. “Tutarlı sistem”den kasıt, içinde mantıksal çelişkiler barındırmayan bir sistemdir.

Matematikte hangi aksiyomların “en temel” olması gerektiği üzerine yapılan tartışmalar oldukça yaygındır. Gödel’in teoremleri, bu tartışmalarda önemli bir uyarı niteliğindedir: Her sistemin bir sınırı vardır. Hiçbir matematiksel yapı, kendi doğruluğunu tamamen kanıtlayamaz.

8) Asal Sayı Teoremi

Asal sayılar üzerine birçok teorem vardır. Ancak bunlar arasında en çok dikkat çekeni Asal Sayı Teoremi (Prime Number Theorem) olarak bilinmektedir. Bu teorem, asal sayıların sayı doğrusundaki dağılımını açıklar. Daha kesin bir ifadeyle, belirli bir doğal sayı N verildiğinde, N’den küçük asal sayıların sayısı yaklaşık olarak N / log(N) kadardır.

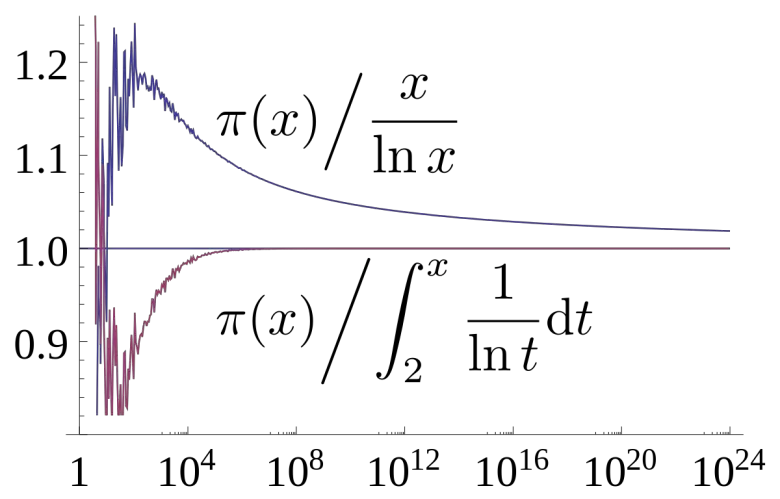
Bu fikir, 19. yüzyıl ortalarında ortaya atılan düşüncelere dayanır. Fransız matematikçiler Jacques Hadamard ve Charles Jean de la Vallée Poussin, 1898 yılında teoremi birbirlerinden bağımsız olarak kanıtladılar. O zamandan beri bu kanıt birçok kez yeniden yazılmış, sadeleştirilmiş ve farklı biçimlerde sunulmuştur. Ancak teoremin önemi ve etkisi giderek artmıştır.

Günümüzde asal sayılarla çalışan modern bilgisayar programları bu teoreme dayanır. Asallık testleri, şifreleme sistemleri ve dijital güvenliğin büyük bölümü bu temel sonuç üzerine kuruludu

9) Polinomların Radikallerle Çözülmesi

Lisede öğrendiğimiz ikinci dereceden denklemler için çözüm formülünü hatırlarsınız. Ezberlemesi zor olsa da kapalı bir formüle sahip olması oldukça kullanışlıdır. Benzer şekilde, üçüncü ve dördüncü dereceden denklemler için de çözüm formülleri vardır. Ancak bu formüller hem çok daha karmaşık hem de kullanımı zordur. Ancak beşinci dereceden itibaren (ve daha yüksek dereceli) denklemler için böyle genel bir formül yoktur.

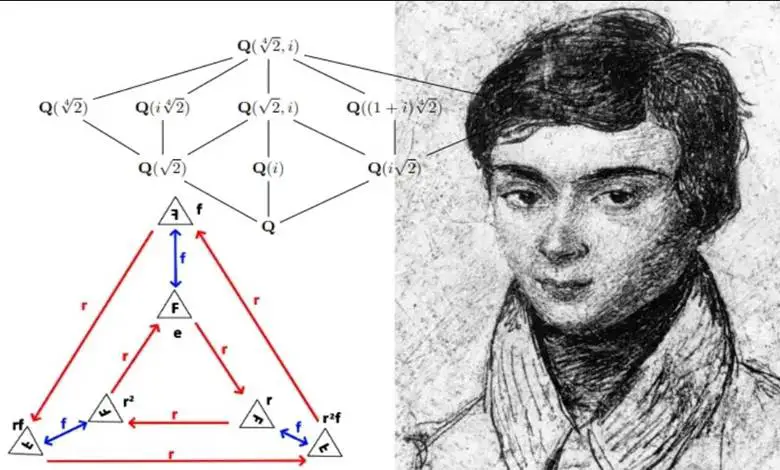
Fransız matematikçi Évariste Galois’nın dehası, dünya tarafından ancak ölümünden sonra fark edilmeye başladı. 1832’de, henüz 20 yaşındayken bir düelloda hayatını kaybetti. Galois’nın fikirleri ölümünden sonra onlarca yıl boyunca tam olarak anlaşılamadı. Ancak zamanla bu düşünceler, bugün Galois Teorisi olarak bilinen büyük bir matematiksel yapıya dönüştü.

Bu teorinin temel sonuçlarından biri, bir polinomun “köklerle çözülebilmesi” için gerekli koşulları açıklar. “Köklerle çözmek” ikinci dereceden denklemler için kullanılan klasik kök formülü gibi, kapalı bir çözüm formuna sahip olmak anlamına gelir.

Galois, dördüncü dereceye kadar olan tüm polinomların bu koşulları sağladığını gösterdi. Ancak beşinci dereceden itibaren durum değişir: Bazı denklemler bu koşulları karşılamaz. Bu nedenle, dördüncü derecenin ötesinde tüm polinomlar için geçerli genel bir çözüm formülü yoktur.

Sonuç Olarak;

Bir zamanlar cevabı bilinmeyen bu dokuz zor matematik problemi, bugün çözülen sorular arasında yer alıyor. Yine de hâlâ çözüm bekleyen pek çok problem var. Matematiği etkileyici kılan da aslında budur.

Kaynaklar ve İleri Okumalar