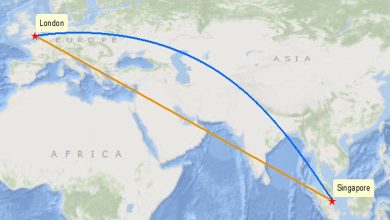
Hepimiz düz bir çizginin iki nokta arasındaki en kısa yol olduğunu kabul ederiz. Peki, bu yol her zaman en hızlı olan mıdır? Bu soruya aşina olmayanlar için, Brakistokron problemi ve bu probleme verilen ilginç yanıt olan Brakistokron eğrisiyle tanışmak faydalı olacaktır.

Aşağıdaki görselde gördüğünüz A ve B noktalarının arasında bir eğik düzlem olduğunu ve bir topu sadece yerçekimi etkisi (sürtünme veya hava direncinin olmadığı varsayılarak) ile A noktasından B noktasına en hızlı biçimde göndermek istediğinizi düşünelim.
Bu iniş süresini en aza indirecek eğrinin şekli nedir? Bu problem, matematik tarihinde Brakistokron problemi olarak bilinir. Yunanca kökenli iki kelimeden oluşur: “Brakhistos” (en kısa) ve “Kronos” (zaman). Bu haliyle, brakistokron kelimesi doğrudan “en kısa zamanda” gerçekleşen hareket anlamına gelir.

Brakistokron problemi, 1696 yılında Johann Bernoulli tarafından ortaya atılan açık bir meydan okumaydı. Kendisini devrinin en yetkin matematikçisi olarak gören Johann, bu soruyla hem kardeşine hem de Leibniz’e ve artık matematikle aktif olarak ilgilenmeyen yaşlı Isaac Newton’a üstünlüğünü kanıtlamak istiyordu.
Johann Bernoulli, brakistokron problemini Acta Eruditorum dergisinde yayımladı. İddiasına göre Bernoulli bu problemi iki haftalık bir çalışma sonunda çözmüştü. Şimdi de diğer matematikçileri çözüme dahil etmek, biraz da ne kadar iyi bir matematikçi olduğunu göstermek istiyordu Başta çözüm süresi olarak altı ay belirlemişti, ancak Leibniz’in önerisiyle bu süre uzatıldı..
Sonuçta beş kişi bu problemi başarıyla çözdü: Isaac Newton, Jacob Bernoulli, Leibniz, Guillaume de l’Hôpital ve sorunun sahibi Johann Bernoulli.
Brakistokron Problemi İçin Johann Bernoulli’nin Bulduğu Çözüm
Johann Bernoulli, brakistokron problemini çözerken oldukça zekice bir benzetme kullandı ve parçacığın izlemesi gereken yolun bir sikloid olduğunu gösterdi. Arşimet’in kütle ve kaldıraç yasalarını soyut geometrik şekillere uygulaması gibi, Bernoulli de yerçekimiyle ilgili bu problemi, ilk bakışta alakasız görünen ışığın kırılma yasalarıyla çözdü.

Bir bisiklet tekerleğinin kenarına küçük bir ışık taktığınızı hayal edin. Şimdi uzaktan bir yerden, bisikletin hareketi esnasında nasıl bir şekil ortaya çıktığına bakın. Göreceğiniz şey aşağıdaki görseldekine benzeyecektir. Bir doğru boyunca dönerek ilerleyen bir çemberin üzerindeki sabit bir noktanın takip ettiği yola sikloid eğrisi denir.
Aslında brakistokron problemini ilk ortaya atan kişi Johann Bernoulli değildi. 1638 yılında Galileo da bu soruyu sormuştu. Ancak çözümünde yanıldı. Yolun en kısa sürede tamamlanacağı şeklin bir çember yayı olduğunu düşünüyordu.
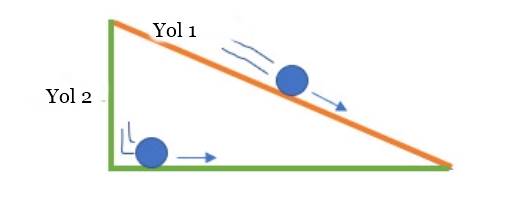
Çözümün ayrıntılarına geçmeden önce, şekle bir kez daha dikkatle bakalım. Bu şekil, sorunun doğasını ve doğru yolun ne olması gerektiğini daha iyi anlamamıza yardımcı olacaktır. Görselde, topun iki farklı yoldan yuvarlanma seçeneğini görüyorsunuz.
Top eğimli bir düzlemde yavaş yavaş hız kazanır. Yerçekimi etkili olsa da, bu etki sınırlıdır. İkinci yol ise, topun başlangıçta serbest düşüş yapmasına olanak tanır. Bu durumda top, daha yolun başında yüksek bir hıza ulaşır.
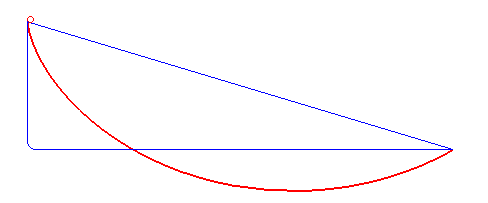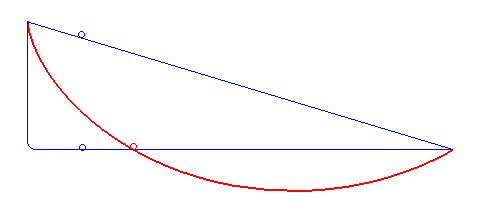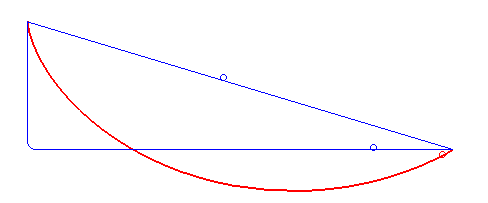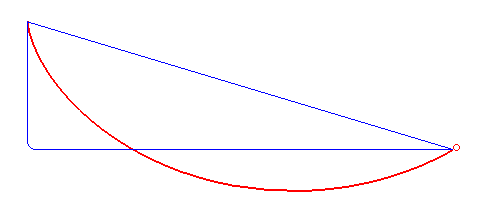
İkinci yol, ilkine göre daha hızlıdır, ancak serbest düşüş sonrası aniden yatay harekete geçmek fiziksel olarak mümkün değildir. Peki ya bu iki yolun özelliklerini birleştirsek? Hem serbest düşüşteki hızlı ivmeyi hem de kısa mesafeyi bir araya getirecek bir yol mümkün mü? Aslında bu sorunun cevabı aşağıdaki şekilde karşınızda: Brakistokron eğrisi.
Brakistokron Problemi İle Snell Yasası Neden İlişkilidir?
Kırılma, ışığın bir saydam ortamdan başka bir saydam ortama geçerken yön değiştirmesidir. Bu temel fizik yasası, merceklerin çalışmasından büyüteçlere, gökkuşaklarından gözlerimize kadar pek çok optik olgunun arkasındaki prensiptir.
Her saydam maddenin — örneğin hava, su ya da camın — kendine özgü bir kırılma indisi vardır. Işık, bu maddelerden birine belirli bir açıyla girdiğinde hızında bir değişiklik olur; bu da ışığın yön değiştirmesine yol açar. Örneğin, ışık havadan suya geçerken yavaşlar ve dolayısıyla farklı bir açıyla yoluna devam eder.
Snell Yasası, ışığın iki farklı ortam arasındaki sınırı geçerken izlediği yolu, her ortamda ışığın yayılma hızıyla ilişkilendirir. Bu yasa, kırılma olayının matematiksel temelini oluşturur.
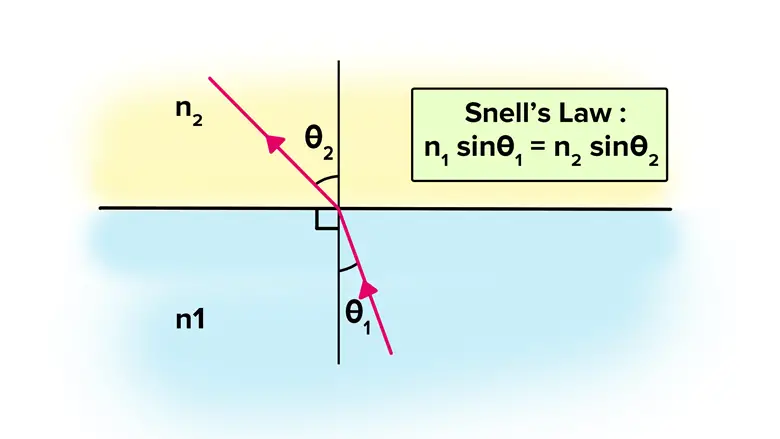
Işık her zaman Snell yasasına uyar ve kırılır çünkü hedefine en kısa yoldan ulaşmak ister. Brakistokron problemini çözmek için Bernoulli bu gerçeği fark edecekti.
Bernoulli, parçacığın düşüş hareketini anlamak için ışığın farklı maddelerden geçerken nasıl davrandığını örnek aldı. Bildiğimiz gibi, ışık bir ortamdan diğerine geçtiğinde hızı değişir. Bernoulli, ışığın geçtiği ortamları özel bir sırayla yerleştirdi: Her bir ortamda ışığın hızı, bir önceki ortama göre biraz daha fazlaydı. Böylece ışık, sanki yukarıdan aşağı doğru düşüyormuş gibi, giderek hızlandı.
Bu hız artışı, tam olarak yerçekimiyle düşen bir cismin hız kazanma biçimine benziyordu. Çünkü ışığın hızındaki artış, yüksekten olan uzaklığın kareköküyle orantılı olacak şekilde ayarlanmıştı. Sonuç olarak, ışığın bu ortamlar arasındaki en hızlı geçiş yolu, aslında bir parçacığın A noktasından B noktasına en kısa sürede ulaşacağı eğriyle aynı hale gelmişti. Bernoulli, böylece ışığın kırılma davranışını kullanarak brakistokron problemini çözmeyi başardı.
Sonuç Olarak
Bu çözüm, fizik tarihindeki en zarif fikirlerden biridir. Işığın davranışını kullanarak, yalnızca yerçekimiyle düşen bir cismi anlamaya çalışmak hem şaşırtıcı hem de son derece etkili bir yaklaşımdır. Bernoulli’nin bu özgün fikri, onu 17. yüzyılın en parlak matematikçileri arasında efsanevi bir yere taşımıştır.
Kaynaklar ve ileri okumalar:
- Is The Shortest Path Always The Fastest?; https://www.scienceabc.com/
- The brachistochrone problem; Bağlantı: https://mathshistory.st-andrews.ac.uk/
- Gómez-Aíza, S & Gómez, Raúl & Marquina, Vivianne. (2006). A simplified approach to the brachistochrone problem. European Journal of Physics. 27. 1091. 10.1088/0143-0807/27/5/008.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel