Mantıkta geleneksel sistemler, uzun süredir akıl yürütmenin temel dayanağı olarak kabul edilir. Ancak bu sistemlerin kusursuz olduğu düşüncesini sorgulayan bir bilmece vardır: Sorites Paradoksu.

Sorites Paradoksu, klasik mantığın sınırlarını gösteren bir bilmecedir. Bu noktada, geleneksel mantık sistemleri düzgün işlememeye başlar. Bu gizemli paradoks, küçük değişikliklerin hiçbir fark yaratmıyormuş gibi göründüğü ama sonunda her şeyi değiştirdiği durumlarda ortaya çıkar.
Sorites Paradoksu Nedir ve Nasıl Ortaya Çıkmıştır?
Sorites Paradoksu, sınırları belirsiz kelimelerin yarattığı anlam bulanıklığını konu alan bir felsefi bilmecedir. Yaklaşık MÖ 400 yılında Yunan filozof Miletli Eubulides tarafından ortaya atılmıştır. Bu paradoks, ikili mantığın yani doğru–yanlış temelli düşünmenin, gerçek dünyanın kademeli değişimlerini açıklamakta neden yetersiz kaldığını gösterir.

Paradoksun özü, küçük değişimlerin fark edilmese de büyük sonuçlara yol açabileceği fikrine dayanır. Bir kum yığını örneğini ele alalım: Tek bir kum tanesi “yığın” oluşturmaz. Bir tane daha eklendiğinde de sonuç değişmez. Eğer her ekleme aynı şekilde etkisizse, hiçbir zaman bir “yığın” oluşmaması gerekir.
Bu sonuç, sezgilerimizle açıkça çelişir. Çünkü günlük hayatta kum yığınlarını, kar yığınlarını ya da yaprak yığınlarını rahatlıkla ayırt ederiz. Paradoks tam da bu noktada “belirsiz tanımlar” sorununa dikkat çeker. Yani sınırları kesin olmayan kelimelerin, gerçek dünyayı tanımlamada nasıl zorluklar yarattığını gösterir.

Bir şeyin miktarı değiştiğinde tam olarak ne zaman başka bir şeye dönüştüğünü belirlemek zordur. Kaç tane kum tanesi eklendiğinde bir yığın oluşur? Ya da kaç saç teli döküldüğünde bir insan “kel” sayılır? Bu dönüşümde hangi an ya da hangi saç teli belirleyicidir?
Sorites Paradoksu, nesneleri kesin kategorilere ayırma eğilimimizi sorgular. Dünyadaki pek çok şey, “evet” ya da “hayır” gibi net yanıtlarla açıklanamayacak kadar kademeli ve belirsizdir. Paradoks, dilin ne kadar kesin olması gerektiğini ve zihnimizin bu belirsizliklerle nasıl başa çıktığını yeniden düşünmemizi ister.
Peki Aristotelesçi (Geleneksel) Mantık Nedir?
Klasik mantığın, yani Aristotelesçi ya da geleneksel mantığın kökleri, akıl yürütme kurallarını sistemleştiren ilk düşünürlerden biri olan Aristoteles’e dayanır. Bu mantık anlayışı, Batı felsefesinin temelini oluşturur ve yüzyıllardır mantıksal sorgulamanın çerçevesini belirler.

Geleneksel mantık, argümanlara odaklanır. Argümanlarsa önermeler kurmayı amaçlayan ifade dizileridir. Ve bu önermeler, öncüllerden sonuçlara doğru geçerli hareketleri yönetmesi beklenen ilkeleri tanımlar.
Özdeşlik ilkesi ise her şeyin kendisiyle aynı olduğunu belirtir. Yani a=a‘dır. Bu basit görünen ilke, nesneler ve kavramlar arasında tutarlılık sağlamak için zorunludur. Matematikte ve mantıkta eşitlik ya da benzerlik ilişkilerini kurarken bu temel kabulden yararlanırız.
Çelişmezlik ilkesi ise bir şeyin kendisine eş olmayan şeye eş olamayacağını söyler. Yani a=a’ olamaz çünkü a’, a’dan farklıdır, onun dışındadır. Üçüncü halin olanaksızlığı ilkesi ise diğer iki ilkeyi tamamlar. Buna göre bir bütün, a ve a olmayanın birleşiminden oluşur. Üçüncü bir durumun varlığı söz konusu değildir. Veya başka bir deyişle, bir önerme ya doğrudur ya yanlıştır. Arada bir değer alamaz.
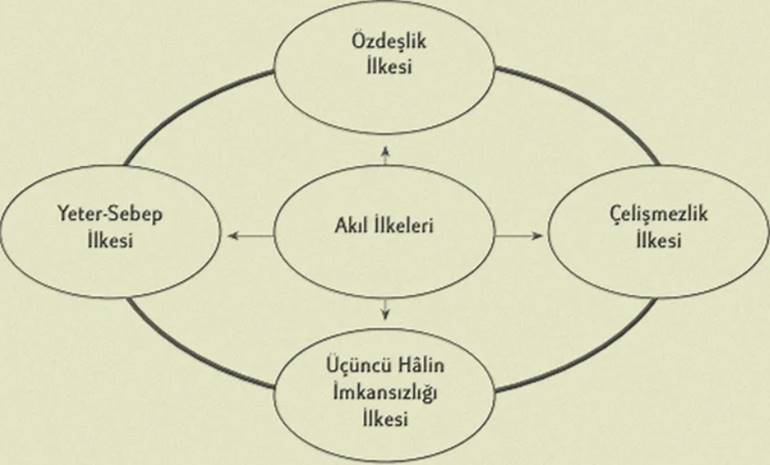
Yine de bu ilkeler, Sorites Paradoksu gibi belirsiz tanımlar içeren durumlarda ikna edici olmaktan uzaklaşır. Çünkü bu tür örnekler, kelimelerin anlam sınırlarının bulanık olduğu durumlarda klasik mantığın katı kurallarının ne kadar geçerli olduğunu sorgulatır.
Sorites Paradoksunun Çözümüne Yönelik Yaklaşımlar
Az önce de gördüğümüz gibi geleneksel mantık sahip olduğu belli kısıtlamalar yüzünden Sorites paradoksuna bir cevap sunamamaktadır. Bazı alternatif sistemler bu konuda daha esnektir.
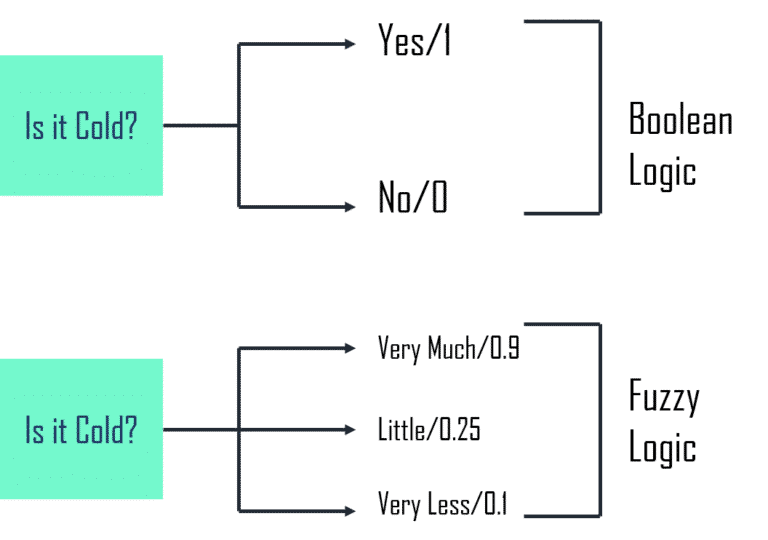
Örneğin bulanık mantık (fuzzy logic) yaklaşımı, önermelerin yalnızca “doğru” ya da “yanlış” olmasını zorunlu kılmaz. Gerçeğin dereceli olabileceğini kabul eder. Bir ifade tamamen doğru, yarı doğru ya da kısmen yanlış olabilir; doğruluk değeri 0 ile 1 arasında bir noktada yer alır. Belirsiz tanımlara sahip kavramlar için bu yöntem oldukça uygundur.
Bulanık mantık, “yığın” ile “yığın olmayan” arasındaki kesin sınırın bulunmadığı Sorites Paradoksu gibi sorunlarda özellikle etkilidir. Bu yaklaşıma göre tek tek kum tanelerini ekledikçe, durum yavaş yavaş değişir ve sonunda bir yığın ortaya çıkar.
Bir diğer alternatif yaklaşım, Kademeciliktir. (Gradualism) Bu görüşe göre nesneleri ya da durumları sınıflandırmak için kesin sınırlar çizmek gerekmez. Özellikler, keskin geçişler olmadan, yavaş ve sürekli biçimde değişebilir. “Kel” ya da “uzun” gibi kelimeleri düşünürsek, bir insanın hangi anda “kel” olduğunu net biçimde belirleyemeyiz. Bu tür kavramlar, doğal olarak kademeli geçişlere dayanır.
Kademecilik ve bulanık mantık, Sorites Paradoksu’na güçlü bir yanıt sunar. Gerçek dünyanın belirsizliklerini anlamak için evet-hayır mantığından daha gelişmiş bir düşünme biçimine ihtiyaç duyduğumuzu gösterir. Bu yaklaşımlar, klasik mantığın göz ardı ettiği gri alanları görünür kılar ve düşünceyi daha esnek bir zemine taşır.
Sonuç olarak;
Sorites Paradoksu ilk bakışta soyut bir mantık sorunu gibi görünür. Ancak, aslında günlük düşünme biçimimizi ve karar alma süreçlerimizi doğrudan etkiler.
Gerçek yaşamda çoğu olay birçok etkenin etkileşimiyle oluşur ve bu etkenler zamanla sürekli değişir. Bu nedenle, dünyanın bu karmaşık yapısını anlamak için klasik mantığın ötesinde, daha esnek düşünme sistemlerine ihtiyaç duyarız.
Kaynaklar ve İleri Okumalar
- Sorites Paradox: Why Traditional Logic Is Not Omnipotent ; Yayınlanma tarihi: 27 Ekim 2024
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





