Kağıt katlayarak matematik yapılabileceğini biliyor muydunuz? Evet, bildiğimiz geometrinin bir çok kavramı yalnızca kağıt katlayarak anlatılabilir. Origami ile daha çok kağıttan turnalar ve tavşanlar yapılsa da geometri dersinde de pek güzel kullanılır. Yazıyı okuyanları bir parça kağıdı alıp, düşünmeye davet ediyorum. Şekildeki gibi katlandığında köşedeki açı her zaman 90° olur. Neden?

Yanıt aşağıdaki şekilde. İnceleyerek anlayabilirsiniz.

Üçgenin İç Açılarının Toplamının 180° Olduğunun İspatı
Öklid geometrisi bazı kabuller üzerine kuruludur. Bir tam dönüşe 360 derece deme konusunda bir ortak anlaşmamız vardır. Böylece yarım dönüş 180 derecedir. Peki, bir üçgenin açılarının toplamının bununla ne ilgisi var?
Bunu göstermenin en kolay ve ikna edici yolu, kağıt bir üçgenin üç köşesini kağıttan ayırmak ve onları bir araya getirip düz bir çizgi oluşturduğunu görmektir. Düz bir çizgi, bir tam dönüşün yarısını temsil eder; yani 180°’yi. Aşağıdaki anlatım size bu konuda fikir verecektir. Burada iki ispat vereceğiz. Birincisi daha basit ve biraz da hileli… Çünkü kağıdı kesmemizi gerektiriyor. (Oysa origamide kağıdı kesmek yok!) Önce şekli inceleyelim.

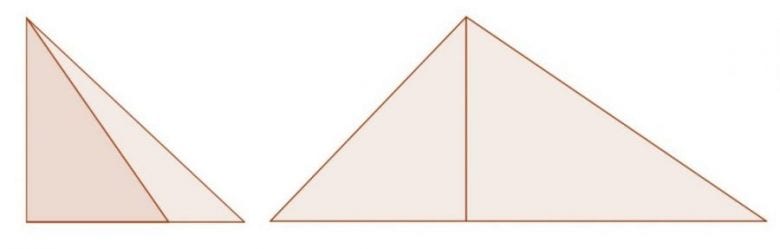
İkinci ispatta kağıdı kesmiyoruz, sadece katlıyoruz. Şekli inceleyiniz. Görüldüğü gibi önce üçgenin tepe noktasından katlayarak, tabana ait yüksekliği buluyor, daha sonra üçgenin sağ ve sol köşelerini yüksekliğin ayağı ile çakışacak şekilde katlıyoruz. Bu şekilde üçgenin açıları, tabanda birleşerek bir doğru açı oluşturur.

Diklik Merkezinin Kağıt Katlayarak Bulunması
Bildiğiniz gibi her üçgenin üç tane yüksekliği vardır. Bu üç yükseklik bir noktada kesişirler. Bu noktaya “diklik merkezi” denir. Diklik merkezi, dar açılı üçgenlerde üçgenin iç bölgesinde, dik açılı üçgenlerde dik köşede, geniş açılı üçgenlerde üçgenin dış bölgesindedir. Bu kadar bilgi yeter. Şimdi katlamaya başlayabiliriz.
Öncelikle, boş bir A4 kağıdına dilediğimiz büyüklükte bir üçgen çiziyoruz. Daha sonra çizdiğimiz bu üçgeni keserek çıkartıyoruz. Şimdi belirlediğimiz herhangi bir kenara ait yüksekliği katlayalım. Bunu aşağıdaki şekilde gösterildiği gibi yapıyoruz.

Yukarıdaki şekilde üçgenin alt kenarlarının üst üste çakışması ve kat yerinin de üst köşeden geçmesi gerekiyor. Bu şekilde yapılan katlama ile alt kenara ait yüksekliği buluruz. Aşağıdaki şekilde solda üçgenin katlanmış halini, sağda ise yeniden açılmış halini görüyoruz. Kat yeri bize üçgenin tabana ait yüksekliğini veriyor.
Şimdi bu işlemi her bir kenar için tekrarlıyoruz. Böylece üçgenin üç yüksekliğini buluyoruz. Ayrıca, kat yerlerinin bir noktada kesiştiğine dikkat ediniz, işte bu nokta üçgenin diklik merkezidir. Bir de üçgeninizin dar açılı üçgen olmasına dikkat ediniz, aksi halde diklik merkezi üçgenin dışına taşacaktır.
Kağıt Katlayarak 60°lik Açı Oluşturma
Bir doğru parçasının ikiye bölünmesi ile başlayalım. Birinci fotoğraftaki [AB] doğru parçasının tam ortası olan noktayı (O noktası) bulmak istiyoruz.

“Çocukluğumuzdan beri yaptığımız bir şey bu!” dediğinizi duyar gibi oluyorum. Gerçekten de öyle. Ancak unutmayalım ki daha yeni başladık. Şimdi 45°lik bir açı oluşturmayı görelim.

Şunu da belirteyim ki kağıdın kare olması gerekmiyor. Herhangi bir dikdörtgen de işimizi görürdü. Ayrıca, şu ana kadar kenarları düzgün bir kağıt kullandık. Peki ya rastgele yırtılmış bir kağıt parçasının kenarını düz hale getirebilir miyiz? (Gülümsediğinizi görür gibi oluyorum.) Bir başka deyişle, kağıttan bir doğru parçası elde edebilir miyiz? Elbette, cevabı biliyorsunuz. Her zaman yaptığımız bir şey bu. Aşağıdaki şekli inceleyiniz.

Tabi aslında burada cetvel kullanmamalıydık, çünkü amaç cetvel kullanmadan, katlayarak bir doğru parçası çizmekti. Zaten biz de cetveli kozmetik amaçlarla kullandık. Yoksa zaten kağıdın kat yeri bir doğru parçası oluşturmuştu. Sıra geldi 90°lik bir açının elde edilmesine… Tahmin edebileceğiniz gibi bu sorunun çözümü de oldukça basit. Bunun için doğru parçası oluştururken kullandığımız kağıt parçasını kullanabiliriz.

İşte 90°lik açıyı da elde ettik. Bu, aynı zamanda verilen bir doğruya dik olan doğrunun da bulunuş yöntemidir. Aşağıdaki şekli inceleyiniz:

Eh, şu ana kadar pek de önemli bir şey yapmadık. Bütün bunlar içgüdüsel olarak zaten bildiğimiz şeylerdi. Şimdi, çözümü pek de kolay olmayan bir soru soralım. Dikdörtgen biçiminde bir kağıt parçası veriliyor. Sadece katlayarak 60°lik bir açı oluşturabilir misiniz? Yanıtımız evet. Bunun nasıl yapıldığı aşağıdaki şekilde açıklanmıştır.

Üçgenin Ağırlık Merkezinin Kağıt Katlayarak Bulunması
Bir üçgenin üç tane kenar ortayı Ağırlık Merkezi olarak adlandırılan bir noktada kesişirler. Bu nokta G harfi( gravity) ile gösterilir. Ağırlık merkezinden asılan üçgenler dengede kalırlar. Cismin tüm ağırlığı bu noktada toplanmış gibi görünür.
Her cismin bir ağırlık merkezi vardır. Basit geometrik cisimlerin ağırlık merkezlerini bulmak da basit bir işlemdir. Örneğin, bir doğru parçasının tam ortasıdır. Bir dikdörtgenin ise köşegenlerinin kesim noktasıdır. Üçgenin ağırlık merkezi ise kenarortaylarının kesim noktasıdır.
Bir cismin ağırlık merkezi, deneysel yollarla da bulunabilir. Kenar ortayların bulunması için üçgenin kenarlarının orta noktaları karşı köşelerle birleştirilir. Ağırlık merkezinin kağıt katlayarak nasıl bulunacağını anlattığımız videomuz burada…
Tıpkı pergel ve cetvel problemleri gibi origami problemleri ve origami ispatları da geometrinin ilginç bir dalını oluşturuyor. Origaminin özellikle matematik öğretiminde önemli bir yeri var–ya da olmalı. Unutmayın, matematiksel düşünme yeteneği kazanmış kişiler hayatta daha başarılı olurlar. Hepinize mutlu ve matematik dolu günler dilerim. Daha fazla fikir için bu yazıya göz atabilirsiniz. Yazının devamında göz atmak isterseniz: Origami İlham Veriyor! Geleceğin Mesleği Origami Mühendisliği
Matematiksel










