Newton’un basit ve yaygın kullanılan optimizasyon yöntemi, sonunda sınırsız karmaşıklıktaki problemlere uygulanabilir hâle geldi.

Matematikte optimizasyon, belirli bir koşul altında en iyi sonuca ulaşmayı hedefleyen bir problem çözme sürecidir. En yaygın haliyle bu, bir fonksiyonun en küçük (minimum) ya da en büyük (maksimum) değerini bulmak anlamına gelir. Daha teknik bir ifadeyle, optimizasyon, bir amaç fonksiyonunun (örneğin maliyet, zaman, enerji, kâr) belirli kısıtlar altında en uygun değerini bulmayı amaçlar.
Her gün, araştırmacılar karşılaştıkları problemlere en uygun çözümleri bulmaya çalışır. Kimi zaman büyük bir hava yolu merkezi nereye kurulmalı sorusunun cevabını ararlar. Kimi zaman da bir yatırım portföyünde riski en aza indirirken getiriyi nasıl en üst düzeye çıkarabileceklerini çözmeye çalışırlar. Ya da trafik ışıklarıyla dur levhalarını ayırt edebilen otonom araçlar geliştirmek isterler.
Matematiksel olarak bu tür sorunlar, bir fonksiyonun minimum değerlerini aramaya dönüştürülür. Ancak bu durumlarda söz konusu fonksiyonlar genellikle doğrudan incelenemeyecek kadar karmaşıktır. Araştırmacılar, bu nedenle minimum değerleri yaklaşık olarak hesaplamak zorundadır.
Bu tür problemleri çözmenin en iyi yollarından biri, Isaac Newton’un 300 yıldan daha uzun bir süre önce geliştirdiği bir algoritmadır. Bu algoritma oldukça basittir. Görmediğiniz bir arazide en alçak noktayı aramaya benzer. Adım attıkça, ihtiyacınız olan tek bilgi; yokuş yukarı mı yoksa aşağı mı gittiğiniz ve eğimin artıp artmadığıdır. Bu bilgilere dayanarak, en düşük değeri nispeten hızlı bir şekilde yaklaşık olarak bulabilirsiniz.

Aradan geçen yüzyıllara rağmen Newton’un yöntemi hâlâ lojistik, finans, bilgisayarla görme ve hatta saf matematik gibi alanlarda temel bir araç olarak kullanılmaktadır. Ancak ciddi bir dezavantajı vardır. Her fonksiyon türünde etkili şekilde çalışmaz. Bu nedenle matematikçiler, yöntemin verimliliğini koruyarak daha geniş fonksiyon sınıflarına uygulanabilmesini sağlayacak yollar üzerinde çalışmayı sürdürmüştür.
Optimizasyon Problemlerini Çözmek İçin Yüzyıllık Bir Teknik
Matematiksel fonksiyonlar, girdileri çıktılara dönüştüren yapılardır. Çoğu durumda bu fonksiyonların en önemli özelliği, çıktıyı en aza indiren girdi kombinasyonunu bulmaktır. Ancak çoğu zaman fonksiyonlar, yüksek dereceli üslere sahip onlarca değişken içerir. Bu durum klasik formüllerle analiz etmeyi imkânsız hale getirir. Bu tür fonksiyonların çözümleri, yüksek boyutlu grafiklerde karmaşık bir manzara oluşturur.
1680’lerde Isaac Newton, karmaşık fonksiyonlarda bile, size en düşük noktayı bulmanızda yardımcı olacak en az iki bilgiye her zaman erişiminiz olduğunu fark etti. Birincisi, fonksiyonun eğimini — yani bir noktadaki dikliğini — veren birinci türevidir. İkincisi ise bu eğimin ne kadar hızlı değiştiğini gösteren ikinci türevdir.
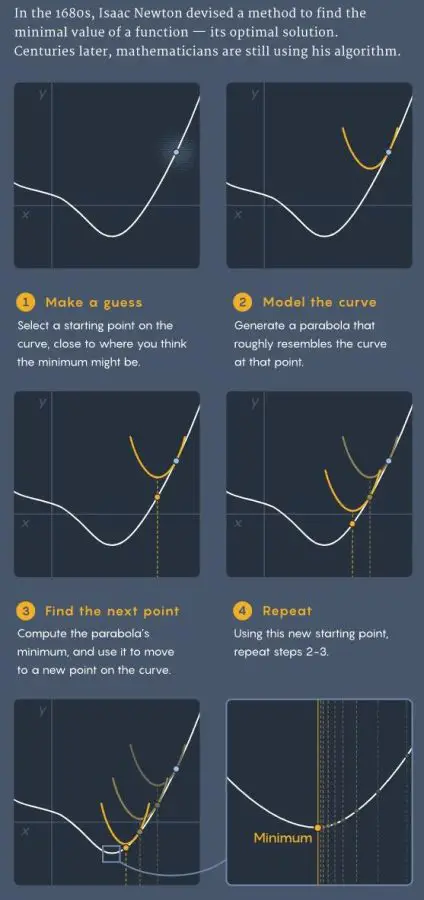
Diyelim ki karmaşık bir fonksiyonun minimumunu bulmaya çalışıyorsunuz. Önce, bu minimuma yakın olduğunu düşündüğünüz bir noktayı seçersiniz. Ardından, bu noktadaki birinci ve ikinci türevleri hesaplarsınız. Bu türevler, fonksiyonun bu noktadaki davranışını temsil eden özel bir ikinci dereceden denklem oluşturmak için kullanılır. Fonksiyon iki boyutlu ise bu denklem bir parabol olur. Daha yüksek boyutluysa, parabole benzeyen bir yapı olan paraboloid olur.
Sonrasında, bu ikinci dereceden denklemin minimumunu hesaplarsınız. Minimumu bulduğunuzda, elde ettiğiniz koordinatları alır ve tekrar orijinal fonksiyona uygularsınız. Böylece, orijinal fonksiyon üzerinde yeni bir noktaya ulaşırsınız. Bu nokta büyük olasılıkla minimuma biraz daha yakındır. Sonra aynı süreci baştan başlatırsınız. Newton, bu işlemi tekrar tekrar sürdürürseniz, sonunda karmaşık fonksiyonun gerçek minimumuna giderek yaklaşacağınızı kanıtladı.
Bugün makine öğrenimi modellerinde kullanılan yinelemeli yöntemler, fonksiyonun gerçek minimumuna doğrusal bir hızla yaklaşır. Newton’un yöntemi ise çok daha hızlı yakınsar. Yani, aynı sonuca ulaşmak için daha az sayıda adım gerekir.
Bir optimizasyon problemini çözmeyi kolaylaştıran özellikler nelerdir?

Aradan geçen yüzyıllar boyunca, matematikçiler Newton’un yöntemini genişletmenin yollarını aradılar. Örneğin, 19. yüzyılda Rus matematikçi Pafnuty Chebyshev, Newton’un yönteminin kübik denklemlerle çalışan bir versiyonunu önerdi. Ancak onun algoritması, fonksiyon birden fazla değişken içerdiğinde işe yaramıyordu.
Bu sorunu, 2021 yılında, şu anda Budapeşte Corvinus Üniversitesi’nde görev yapan Yurii Nesterov ele aldı. Nesterov, herhangi sayıda değişkene sahip fonksiyonların kübik denklemlerle verimli şekilde nasıl yaklaşık olarak çözülebileceğini gösterdi. Ancak yöntemi, daha yüksek dereceli denklemlere genelleştirildiğinde verimliliğini kaybediyordu. Buna rağmen, bu çalışma alanda önemli bir atılım olarak kabul edildi.

Şimdi ise Princeton Üniversitesi’nden Amir Ali Ahmadi, Abraar Chaudhry ve Jeffrey Zhang, Nesterov’un elde ettiği sonucu bir adım daha ileri taşıdı. Geliştirdikleri algoritma, herhangi sayıda değişken ve istenilen kadar türev için geçerli çalışıyor. Üstelik bu genellemelere rağmen hâlâ verimli kalıyor
İki temel nitelik öne çıkar: İlki, denklemin “kase” biçiminde olması, yani konveks yapıda olmasıdır. Böyle denklemler, birden fazla yerine yalnızca tek bir minimum içerir. İkinci özellik, denklemin karelerin toplamı şeklinde yazılmasıdır. Örneğin, 5x² + 16x + 13 ifadesi, (x + 2)² + (2x + 3)² şeklinde kareler toplamı biçiminde yeniden yazılabilir.
Taylor yaklaşımı, karmaşık bir fonksiyonun belli bir noktadaki davranışını basit bir polinomla yaklaşık olarak ifade eder. Fonksiyonun birinci türevi eğimi, ikinci türevi eğimin ne kadar değiştiğini, üçüncü türevi bu değişimin değişimini vs. verir. Taylor yaklaşımı, bu türev bilgilerini kullanarak, fonksiyonun o noktaya yakın bölgede nasıl davrandığını tahmin eden bir polinom üretir.
Ancak bu yaklaşımın bir sorunu vardır. Elde edilen yaklaşık fonksiyon her zaman konveks veya kareler toplamı şeklinde çıkmaz. Bu da onu minimize etmeyi zorlaştırır. Ahmadi, Chaudhry ve Zhang’ın yaptığı şey, Taylor yaklaşımını küçük ama bilinçli bir biçimde değiştirmek oldu. Böylece hem konvekslik hem de kareler toplamı özelliği elde edildi. Böylece Newton’un yöntemi, verimli şekilde çalışabilir hale geldi.
Sonuç Olarak
Newton’un yöntemine dayanan bu yeni algoritma, her adımda yüksek işlem gücü gerektirdiği için henüz günlük uygulamalarda tercih edilmiyor. Otonom araçlar, yapay zekâ sistemleri ve benzeri alanlarda şimdilik daha hafif çözümler kullanılıyor. Ancak bu yöntem, optimizasyona farklı ve güçlü bir bakış sunuyor. Hesaplama teknolojisi ilerledikçe, bu algoritma ileride çok daha geniş bir kullanım alanına sahip olabilir. Ahmadi’ye göre, teoride daha hızlı olan bu yöntem gelecekte pratikte de öne çıkacak.
Kaynaklar ve ileri okumalar
- Three Hundred Years Later, a Tool from Isaac Newton Gets an Update. Yayınlanma tarihi: 24 Mart 2025. kaynak site: Quanta Magazine. Bağlantı: Three Hundred Years Later, a Tool from Isaac Newton Gets an Update
- Nesterov, Yurii. (2019). Implementable tensor methods in unconstrained convex optimization. Mathematical Programming. 186. 1-27. 10.1007/s10107-019-01449-1.
- Ham, Yoonmee & Chun, Changbum & Lee, Sang-Gu. (2009). Some higher-order modifications of Newton’s method for solving nonlinear equations. Journal of Computational and Applied Mathematics. 222. 477-486. 10.1016/j.cam.2007.11.018.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel