Bir matematik problemini güzel yapan şeylerden birisi, onu çözmeye çalışırken bazı beklenmedik keşifler yapma potansiyelinizin olmasıdır. En azından Esther Klein’ın 1933’teki deneyimi böyleydi. Üstelik bu keşif beklenmedik bir biçimde mutlu bir sonla bittiği için matematikte önemli bir probleme de adını verecekti.

1933 yılında Budapeşte’de yaşayan 23 yaşındaki Esther Klein, iki yakın arkadaşı Paul Erdős ve George Szekeres’e düşündürücü bir matematik problemi sundu. Soru şuydu: Eğer beş nokta seçilir ve bu noktaların hiçbiri üçlü olarak aynı doğru üzerinde yer almazsa, bu noktalardan her zaman dördü birleştirilerek dışbükey bir dörtgen oluşturulabilir mi?
Klein, bu ifadenin doğru olduğunu ve kanıtladığını biliyordu; ancak problemi arkadaşlarıyla paylaşarak onları da bu düşünsel yolculuğa davet etti.
Erdős ve Szekeres kısa süre içinde bu sonucun gerçekten doğru olduğunu gösterdi. Ancak burada durmadılar. Akıllarına şu soru takıldı: Madem beş nokta dışbükey bir dörtgen için yeterli, peki ya beşgen için kaç nokta gerekir? Ya da onbirgen için? Bu ilk bulmaca, onları çok daha geniş kapsamlı bir matematiksel soruya yöneltti.

Neden Mutlu Son?
1935’te Erdős ve Szekeres, mutlu son probleminin ilk örneklerini çözüme kavuşturdu. Üçgen oluşturmak için üç, dörtgen için beş, beşgen için ise dokuz noktanın yeterli olduğunu gösterdiler. Aynı makalede, dışbükey n kenarlı bir çokgen çizmek için gerekli minimum nokta sayısı için genel bir formül de önerdiler 2(n−2) + 1. Erdős, her zamanki gibi bu tahmini kanıtlayacak kişiye 500 dolarlık bir ödül koydu.
Zamanla bu problem, sadece matematiksel içeriğiyle değil, arkasındaki hikâyeyle de hatırlanır oldu. Tartışmalar, yalnızca bir matematik sorusunu değil, bir aşkı da başlattı. Esther Klein ve George Szekeres, bu fikir alışverişinden birkaç yıl sonra, 13 Haziran 1937’de evlendi. Bu yüzden problem, “mutlu son problemi” adıyla anıldı.
Ama bu sezgiyi kesin bir biçimde kanıtlamak uzun yıllar kimsenin başaramadığı bir iş olarak kaldı. Yalnızca bir adım atılabildi: 2006’da Szekeres ve Lindsay Peters, dışbükey bir altıgen çizmek için en az 17 noktanın gerektiğini ispatladı. Bu sessizliği bozan ise University of Illinois, Chicago’dan Andrew Suk oldu. Suk, Erdős ve Szekeres’in formülünü destekleyen güçlü matematiksel kanıtlar ortaya koydu.
Mutlu Son Problemi Nedir?
Mutlu son problemi, basit bir dışbükey çokgenden başlayarak şeklin kenar sayısını adım adım artırmayı konu alır. Beş noktanız olduğunu düşünün; bu, dört tanesini birleştirerek mutlaka dışbükey bir dörtgen oluşturabileceğiniz anlamına gelir. Peki ya bu şekli beşgene, altıgene ya da daha fazlasına çevirmek isteseniz?
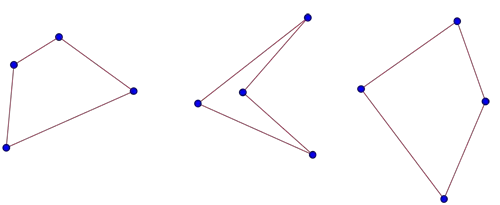
İşte asıl soru burada ortaya çıkar. Kenar sayısı arttıkça, her zaman dışbükey bir çokgen oluşturmak için kaç noktaya ihtiyaç vardır? Mutlu son problemi, bu soruya net bir yanıt bulmaya çalışır.
Erdős ve Szekeres, önerdikleri formülü ispatlayamadı ama bu sonuca ulaşmanın muhtemel yolunu iyi biliyorlardı. 1935 tarihli makalelerinde, dışbükey çokgenleri bugün “kap” ve “kupa” olarak adlandırılan iki yapının birleşimi olarak tanımladılar.
Kupa, “u” harfine benzeyen bir noktalar kümesidir ve çokgenin alt kısmını oluşturur. Kap ise “n” harfi şeklindeki bir küme olup üst kısmı meydana getirir. Bu yaklaşım, dışbükey çokgenlerin nasıl yapılandığını anlamak ve ispat sürecinde yol almak için önemli bir kavramsal çerçeve sundu.

Bir dışbükey çokgeni “kupa” ve “kap” parçalarının birleşimi olarak düşünmenin avantajı, bu parçaları büyütmenin çokgenin tamamını büyütmekten daha kolay olmasıdır. Örneğin, beş noktadan oluşan dışbükey bir kap varsa, altıncı noktayı yapının uçlarından birine ekleyerek onu her zaman genişletebilirsiniz.
Ancak aynı şeyi doğrudan beş kenarlı bir dışbükey çokgen için söylemek zordur. Altıncı bir noktayı nereye ekleyeceğinizi ve bu sırada dışbükeyliği nasıl koruyacağınızı belirlemek çok daha karmaşıktır. Bu yüzden, dışbükey çokgenleri daha küçük, yapıların birleşimi olarak görmek ispat açısından büyük kolaylık sağlar.
Mutlu Son Problemi Nasıl Çözüldü?
1935’te Erdős ve Szekeres, bugün “kupa-kap teoremi” olarak bilinen önemli bir matematiksel sonucu ortaya koydu. Bu teorem, belirli büyüklükte bir “kupa” (U şeklinde noktalar) ya da “kap” (n şeklinde dizilim) oluşumunu garanti altına almak için gereken minimum nokta sayısını belirliyor.
Teoreme göre, düzlemde 4n nokta varsa, bu noktalar mutlaka n kenarlı dışbükey bir çokgen oluşturacak şekilde gruplanabilir. Ancak bu sayı, Erdős ve Szekeres’in önerdiği ilk formülden çok daha büyük. Çözüm teoride mümkün olsa da pratikte verimsiz hale geliyor.
Erdős ve Szekeres, kup ve kapları verimli biçimde birleştirebilirlerse, formüllerini ispatlayabileceklerini düşündü. Fakat bunu başarmak zordu. İki şekli birleştirmek için, kapın kupun tam üstünde yer alması gerekiyordu. Yani kapta seçilen iki noktayı birleştiren her doğru, kupun tüm noktalarının üzerinde kalmalıydı. Bu şart sağlanmadığında ortaya çıkan şekil dışbükey olmuyordu.
Matematikçiler bu engeli uzun süre aşamadı. Kup ve kapın doğru konumlandığını ispatlamak için yapılan kısıtlamalar, yapıların boyutunu küçülttü. Bu da birleşimden elde edilen kazancı azalttı. Teorik olarak mantıklı görünen bu yöntem, pratikte yetersiz kaldı. Ancak Andrew Suk bu kilidi açtı.
Suk, çalışmasında “Ramsey kuramı”na başvurdu. Bu kuram, büyük ve dağınık kümelerde mutlaka düzenli bir alt küme bulunacağını söyler. Yani noktaları düzleme nasıl yerleştirirseniz yerleştirin, sayı yeterince büyükse, dışbükey bir n-gen oluşturacak düzgün bir alt küme mutlaka ortaya çıkar. Erdős ve Szekeres bu fikri daha önce sezgisel olarak fark etmişt. Ama Suk bunu kanıtla temellendirdi.
Andrew Suk’un çalışması, Erdős ve Szekeres’in öne sürdüğü formülün neredeyse kesin olarak doğru olduğunu gösteriyor. Tam bir ispat sunmasa da, bu sezgiyi güçlü biçimde destekliyor. Suk’un kanıtı, problem için daha önce bilinen üst sınır olan 4n nokta değerini aşağı çekiyor. Üstelik bu yeni sınır, nokta sayısı büyük olduğunda, Erdős ve Szekeres’in formülüne çok yaklaşıyor.
Sonuç Olarak;
Ne Erdős ne de Szekeres artık hayatta. Erdős 1996’da öldü, ama kurduğu para ödülleri hâlâ verilmeye devam ediyor. Szekeres ve Esther Klein, 2005’te, doksanlı yaşlarındayken Avustralya’daki Adelaide kentinde bir huzurevine taşındı. 28 Ağustos günü, birbirlerinden yalnızca bir saat arayla hayatlarını kaybettiler. Bu, “mutlu son problemi”nin ortaya atılmasından tam 70 yıl sonraydı.
Kaynaklar ve İleri Okumalar:
- Happy Ending Problem – Numberphile; https://www.youtube.com/
- A Puzzle of Clever Connections Nears a Happy End. Yayınlanma tarihi: 30 Mayıs 2017; Bağlantı: https://www.quantamagazine.org/a
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





