Bir pipette kaç delik vardır? Bir mi, yoksa iki mi? İlk bakışta bu sorunun yanıtı oldukça basit gibi görünebilir. Ancak konuya biraz daha yakından bakıldığında, bu sorunun düşündüğünüzden çok daha tartışmalı olduğu ortaya çıkar.

Kimileri pipetin yalnızca bir deliği olduğunu savunurken, bazıları iki deliği bulunduğunu iddia eder. Hatta pipetin sonsuz sayıda deliğe sahip olduğunu ya da hiç deliği olmadığını ileri sürenler bile vardır!
“Delik” kelimesi, konuya uzak biri için genellikle gündelik yaşamda karşılaşılan basit boşlukları çağrıştırır. Ancak matematikçiler için bu kavram, çok daha farklı bir anlam taşır ve topoloji adı verilen matematik dalıyla ilişkilidir.
Ne var ki, topolojide bile “delik” kavramı tek bir şekilde tanımlanmaz. Farklı yaklaşımlar, delik sayısının nesneye göre değil, tanıma göre değişmesine neden olur. Bu da “Bir pipetin kaç deliği vardır?” sorusunu, beklenenden çok daha karmaşık bir hale getirir.

Matematiksel Anlamda Delik Nedir?
On dokuzuncu yüzyılın sonlarına doğru, matematikçiler klasik geometriden farklı bir yaklaşım geliştirmeye başladılar. Bu alana başlangıçta “analysis situs” — yani konumun analizi — adı verildi. Ancak kısa sürede, bugün de kullanılan “topoloji” terimi yerleşti.
Geometride, daireler ve çokyüzlüler gibi şekiller katı ve sabittir; belirli uzunluklara, açılara ve alanlara sahiptir. Ancak topolojide şekiller esnek kabul edilmektedir. Örneğin, geometrik olarak birbirinden farklı olan bir küre ile bir küp, topolojik açıdan aynı sınıfa girer.
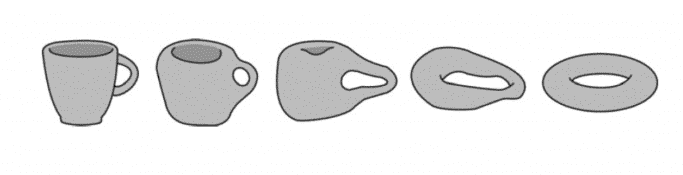
Bu konudaki en bilinen örneklerden biri, bir simidin topolojik olarak bir kahve fincanıyla aynı kabul edilmesidir. Bu benzetmede değişmeyen unsur, “delik”tir. Simidin ortasındaki delik, kahve fincanının sapındaki delikle yer değiştirir. Başka bir deyişle, delik yok olmaz; yalnızca biçim değiştirir. Topolojik olarak iki nesnenin eşdeğer sayılabilmesi için, sahip oldukları delik sayısının aynı olması gerekir.
Topolojide Delik Sayısı İle İlgili Sorun Nedir?
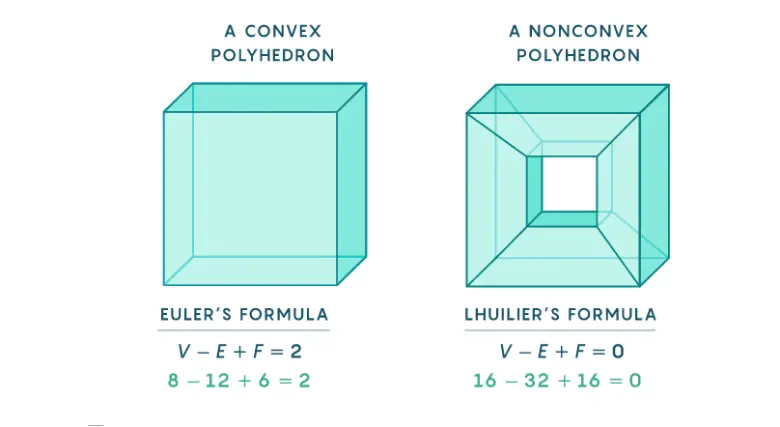
Topolojinin kökeni, Descartes’ın 1639’da düzgün çokyüzlüler üzerine düşünürken fark ettiği ilginç bir sayısal düzene dayanır. Descartes düzgün çokyüzlülerle ilgilenirken dikkat çekici bir sayısal düzen fark etti. Küpte 6 yüz, 12 ayrıt ve 8 köşe vardır; 6 − 12 + 8 = 2 eder.
On iki yüzlüde 12 yüz, 30 ayrıt ve 20 köşe vardır; 12 − 30 + 20 = 2 olur. Yirmi yüzlüde 20 yüz, 30 ayrıt ve 12 köşe vardır. Yani 20 − 30 + 12 yine 2 verir. Aynı ilişki düzgün olsun olmasın, herhangi bir çokyüzlü için geçerlidir. Yüz sayısı F, ayrıt sayısı E ve köşe sayısı V ise F − E + V = 2 olur.
Descartes bu bağıntıyı küçük bir merak unsuru olarak gördü ve yayımlamadı. Oysa daha sonra matematikçiler bu basit eşitliği, yirminci yüzyıl matematiğinin büyük başarı alanlarından biri olan topolojinin ilk adımlarından biri olarak değerlendirdi. Bu bağıntıyı kanıtlayıp yayımlayan kişi ise, tarihin en üretken matematikçisi olan Euler olacaktı.
Euler formülü önemli bir sonuç verir. Bir cismi basitleştirirken yüzleri birleştirebiliriz ya da ayrıt ve köşeleri kaldırabiliriz. Her kaldırılan yüzle birlikte bir ayrıt da kaldırılırsa veya her kaldırılan köşeyle birlikte bir ayrıt silinirse F − E + V değeri değişmez.
Ancak burada önemli bir ayrıntı vardır. Descartes’ın bağıntısı her cisim için geçerli değildir. Bunun en tanıdık karşı örneklerinden biri bir resim çerçevesidir. Dikdörtgen kesitli dört tahta parçanın köşelerde 45 derecelik kesimlerle birleştirildiğini düşünelim.
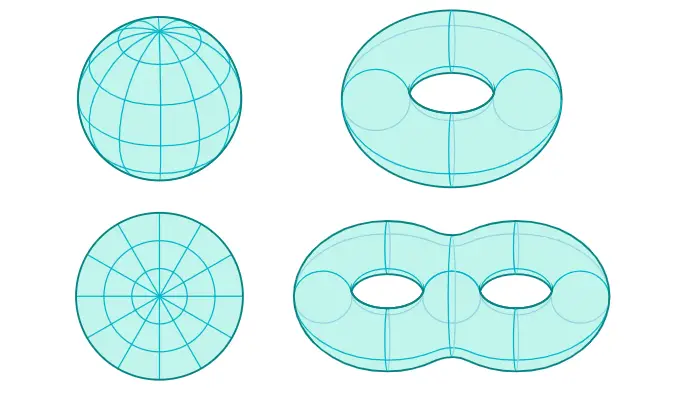
Demek ki resim çerçevesi ile küp arasında temel bir fark vardır ve F − E + V değişmezi bu farkı ortaya çıkarır. Bu fark da temelde topolojilerinden kaynaklanmaktadır. Aynı durum bir küre ve bir torus için de geçerlidir.
Bir Pipetin Kaç Tane Deliği Vardır?
Torusa benzeyen, ancak iki ya da daha fazla deliği olan cisimler de vardır. İki delikli torusa dönüştürülebilen her cisim için F − E + V = −2 olur. Üç delikli torusa dönüştürülebilenler için bu değer −4’tür. Genel olarak g delikli bir torusa dönüştürülebilen her cisim F − E + V = 2 − 2g bağıntısını sağlar. Buradaki g, delik sayısını ifade eden “genus” terimidir.
Böylece yüz, ayrıt ve köşe sayıları gibi nicel veriler ile cismin delik taşıması gibi nitel bir özellik arasında doğrudan bir bağ kurulur. F − E + V ifadesine cismin Euler karakteristiği denir.
Delik sayısını saymak nicel bir işlemdir, ancak “delik” kavramının kendisi açık ve basit değildir. Deliği cismin bulunmadığı bir uzay bölgesi gibi düşünmek yetersiz kalır; çünkü bu tanım cismin dışındaki tüm uzay için de geçerlidir, ama buna delik demeyiz.
Delik kavramını tanımlamaya çalıştıkça, sezgisel sandığımız bu fikrin aslında oldukça karmaşık olduğu ortaya çıkar. Bu nedenle topoloji, deliği doğrudan tanımlamak yerine, Euler karakteristiği gibi değişmezler aracılığıyla dolaylı biçimde ele alır.
Peki, az önce sözünü ettiğimiz topolojik yaklaşımı pipete nasıl uygularız? Sonuçta bir pipet, aslında silindirin kıvrılıp şekil verilmiş halidir. İlk bakışta, pipetin iki deliği varmış gibi görünebilir. Ancak pipeti diklemesine kesip açtığınızda, bu iki açıklık ortadan kalkar ve geriye yalnızca düz bir dikdörtgen yüzey kalır.
Örneğin bir bardağı düşünelim. Ağzı açıktır ve içine bir şey konulabilir; ancak topolojik açıdan, kulpsuz bir bardakta delik yoktur. Bu nedenle, pipetin iki deliği olduğunu söylemek doğru olmayabilir. O halde, pipette kaç delik vardır?
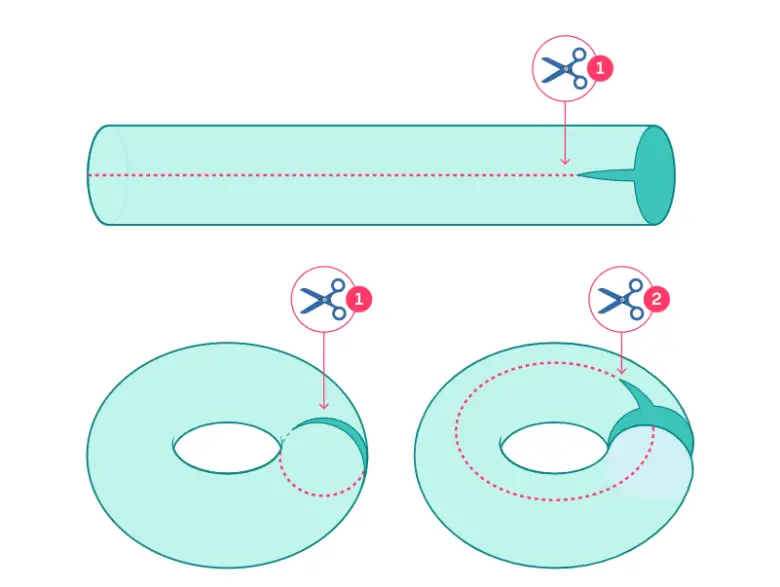
Şimdi pipetin esnek olduğunu hayal edip şeklini değiştirelim. Üstten bastırarak üst ve alt açıklıkları birleştirelim. Bu durumda pipet, bir simide benzer. Bu perspektife göre, pipetin bir deliği olduğunu söyleyebiliriz.
Topolojide Deliğin Alternatif Bir Tanımı Nedir?
İçinde delikler bulunan cisimler yalnızca merak konusu olsaydı büyük bir sorun doğmazdı. Ancak on dokuzuncu yüzyılın sonlarına gelindiğinde bu tür yapılar matematiğin birçok alanında ortaya çıkmaya başladı: karmaşık analizde, cebirsel geometride ve Riemann’ın diferansiyel geometrisinde.
Dahası, yalnızca üç boyutlu cisimler değil, daha yüksek boyutlu benzer yapılar da hem saf hem uygulamalı matematikte önemli hâle geldi. Bu karmaşık tabloyu düzenleyebilmek için genel ve güvenilir bir araç gerekiyordu. Çözüm, değişmezler kavramı oldu.
Bu yaklaşım “delik” kavramını açıkça tanımlama zorunluluğunu ortadan kaldırır. Genelleştirilmiş Euler bağıntısı F − E + V = 2 − 2g biçimindedir. Buradan g = (2 − F + E − V)/2 elde edilir. Yüzleri, ayrıtları ve köşeleri sayıp bu formülde yerine koyarız ve g değerini buluruz. Bu ifade değişmez olduğu için cismi nasıl böldüğümüz sonucu etkilemez. Böylece “delik sayısı”, doğrudan tanımlanmadan hesaplanan bir nicelik olur.
Kaynaklar ve ileri okumalar
- Topology 101: The Hole Truth. Yayınlanma tarihi: 26 Ocak 2021. Bağlantı: Topology 101: The Hole Truth/
- What We Talk about When We Talk about Holes. Yayınlanma tarihi: 25 Aralık 2014; Bağlantı: https://blogs.scientificamerican.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel