Tüm kaotik sistemler, aslında basit matematiksel denklemlerle tanımlanabilir. Ancak bu denklemlerde meydana gelen en küçük bir değişiklik bile, öngörülemeyen ve tekrarlanamayan sonuçlara yol açar. Bu durum, “kelebek etkisi” olarak bilinen kavrama temel oluşturur.

1961’de MIT’den meteorolog Edward Lorenz, hava durumu tahmini için geliştirdiği bir bilgisayar modeline veriler giriyordu. Modelde kullanılan değişkenlerden birinin değeri 0.506127 idi. Lorenz modeli yeniden çalıştırırken bu değeri 0.506 olarak yuvarladı ve kahve almak için odadan çıktı. Döndüğünde, küçücük bir farkın tahminleri tamamen değiştirdiğini gördü.
Bu şaşırtıcı bulgu, kaos teorisinin temelini attı. Lorenz, 1972’de Amerikan Bilimin Gelişmesi Derneği toplantısında bu konuyu anlattığında ünlü sorusunu sordu. “Brezilya’da bir kelebeğin kanat çırpması, Teksas’ta bir kasırgayı tetikler mi?”
Lorenz’in kelebek metaforu, küçük ve önemsiz görünen eylemlerin gelecekte büyük değişimlere yol açabileceğini anlatıyordu. Bu güçlü benzetme, hem bilim insanlarının hem de kamuoyunun hayal gücünü derhal cezbetti.

Edward Lorenz’in kelebek etkisini keşfi, kaos teorisinin gelişmesinde önemli bir dönüm noktası oldu. Bu bulgu, karmaşık ve doğrusal olmayan sistemlerde geleceği tahmin etmenin önündeki ciddi sınırları ortaya koydu.
Kelebek Etkisini Neden Yanlış Anladık?
Kaos teorisinin merkezinde yer alan fikir şudur: Deterministik sistemler başlangıç koşullarına son derece duyarlı olabilir. Başlangıçtaki küçük bir farklılık, zamanla sistemin nasıl evrileceği üzerinde büyük değişimlere yol açabilir.
Üstelik bazı sistemlerde geri besleme döngüleri bulunur. Bu durumda küçük bir fark sistemin içine yeniden işlenir ve ilerleyen süreçte hangi sonuçları tetikleyeceğini kestirmek imkânsız hale gelir. Kısacası, kontrol tamamen elimizden çıkar.
Determinizm felsefede, tüm olayların geçmişteki nedenler tarafından bütünüyle belirlendiği fikrine dayanır. Dolayısıyla bu yasaların varlığı, görünürde rastgeleliğe yer bırakmaz. Ancak kelebek etkisi determinizmi reddetmez; aksine, deterministik sistemlerin içinde ortaya çıkar. Bu da, doğrusal olmayan süreçler nedeniyle küçük farklılıkların, kesin kurallara tabi sistemlerde bile beklenmedik sonuçlar yaratabileceğini gösterir.
Kelebek etkisi kavramı zamanla filmlere konu oldu ve son yıllarda sosyal medyada bir akıma dönüştü. Pek çok kişi, hayatlarının yönünü değiştiren “kelebek etkisi anılarını” paylaşmaya başladı. Ancak bu anlatımlar, Edward Lorenz’in ortaya koyduğu bilimsel kavramı çoğu zaman yanlış yansıtır.
İnsanlar bu terimi genellikle, küçük olayların doğrudan büyük sonuçlara yol açtığı fikriyle ilişkilendirir. Ancak bu yorum, Lorenz’in orijinal kavramından bir ölçüde sapar. Lorenz’in vurguladığı asıl nokta, karmaşık sistemlerin başlangıç koşullarına son derece duyarlı olduğu için öngörülemez olduğudur.
Popüler kültürde basitleştirilse de, kelebek etkisi bilim insanları için hâlâ ciddi bir araştırma konusudur. Çünkü bugün atılan küçük bir adımın, gelecekte nasıl büyük sonuçlar doğurabileceğini anlamak, uzun vadeli öngörüler açısından büyük önem taşır.
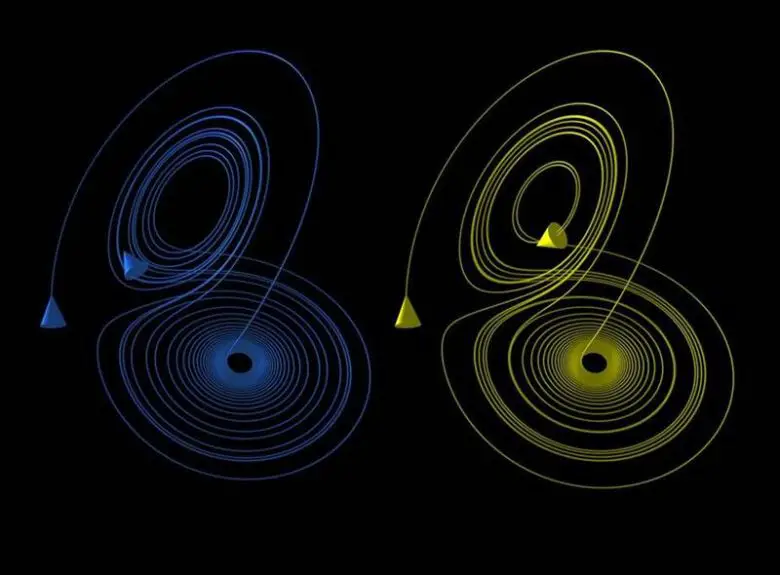
Edward Lorenz’in en önemli katkılarından biri, geliştirdiği modeller ve yöntemlerle kaotik doğayı ve sınırlı öngörülebilirliği anlamamıza ilham vermesidir. Onun çalışmaları, bu alanda yapılan pek çok araştırmanın temelini oluşturmuştur.
Kelebek Etkisi Değişen İklimle Nasıl İlişkilidir?
Kelebek etkisinin en çok öne çıktığı alan hava durumu tahminleridir. Ancak bu kavram, iklim değişikliğini modellemek için de bilim insanlarına önemli bir araç sunar. Son zamanlarda araştırmacılar, yapay zekâyı kullanarak kelebek etkisini simüle etmeyi ve böylece hava tahminlerini iyileştirmeyi amaçladı. Ne var ki yapay zekâ, kelebek etkisini başarılı şekilde modelleyemedi. Bu durum kelebek etkisinin geçersizliğini değil, yalnızca yapay zekânın bu karmaşık kavramı henüz kavrayamadığını gösteriyor.
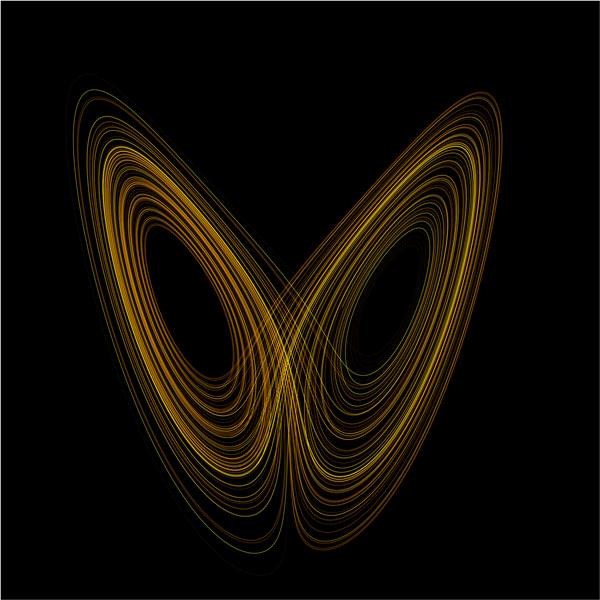
Lorenz’in ve onun kelebek etkisinin bilimsel etkisi hâlâ devam ediyor. Kaos teorisi, fizik, biyoloji, mühendislik, ekonomi ve hatta sosyal bilimler gibi birçok alanda devrim yarattı. Richard Anthes’e göre Lorenz’in geliştirdiği model, geleceğin bugünkü koşullara bağlı olduğu tüm disiplinlerde büyük bir etki oluşturdu.
2011 yılında MIT, Lorenz’in adını taşıyan bir iklim araştırma enstitüsü kurdu. Bu enstitü, doğrudan pratik uygulaması olmayan bilimsel araştırmaları destekliyor. “Temel araştırma” olarak adlandırılan bu yaklaşım, kelebek kanatlarının çırpılması kadar küçük hareketlerin ne kadar büyük sonuçlar doğurabileceğini anlamamıza yardımcı olmayı amaçlıyor.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Mathematical chaos and the butterfly effect: kaynak site: Plus Math. Yayınlanma tarihi: 26 Ocak 2023. Bağlantı: Maths in a minute: Mathematical chaos and the butterfly effect
- Shen, Bo-Wen & Pielke, Roger & Zeng, Xubin. (2024). A Summary of Two Kinds of Butterfly Effects. 10.13140/RG.2.2.32401.24163.
- Selz, T. & Craig, G.. (2023). Can Artificial Intelligence‐Based Weather Prediction Models Simulate the Butterfly Effect?. Geophysical Research Letters. 50. 10.1029/2023GL105747.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





