Mühendislerin birbirleriyle paylaşmayı sevdikleri videolar, sezgisel olmayan ve büyüleyici fiziksel sistemleri tasvir etme eğilimindedir. Muhtemelen siz de bunlardan biri olan havada asılı bir biçimde duran bir masa ile ilgili videoya denk gelmiş olabilirsiniz.
Aşağıda da örneğini görebileceğiniz bu masa ilk bakışta mantığa gerçekten de aykırı gelecektir. Sonucunda bu masa bacaklar yerine ipler üzerinde duruyor gibi gözükmektedir. Bu görüntü ilk bakışta bir illüzyon izlemi verse de aslında gerçektir. Tamamen fiziksel kuvvetlerin dengesi üzerine kuruludur. Bu tarz yapılar tensegrity sayesinde ayakta durmaktadır.

Tensegrity Nedir?
Asma Germe sistemlerin İngilizce kelime kökeni Tensegrity sözcüğüdür. Tensegrity sözcüğü ‘tension’ (çekme) ve ‘integrity’ (bütünlük) sözcüklerinin birleşiminden meydana gelmiştir. Asma germe sistemler, çekmeye çalışan elemanlar ile basınca çalışan elemanların oluşturduğu bir gerilmeler bütünlüğü sistemidir.
Bu kelime ilk olarak efsanevi mimar Buckminster Fuller tarafından alternatif yapısal sistemlerle yaptığı deneyler sırasında kullanılmıştır. Tensegrity sistemler 2 farklı türde öğeden meydana gelmektedir. Bunlar kendinden gerilimli bir yapı oluşturan germe öğeleri ve basınç öğeleridir.

Fuller, vizyonunu birçok kişinin tasarım ve mimaride yeni yönler keşfettiği 1920’lerde geliştirmeye başladı. Ancak 1949’da ilk yapıyı öğrencisi, heykeltıraş Kenneth Snelson meydana çıkardı. Snelson gergin bir naylon kablo ile havada asılı duran iki adet X-şekilli ahşap payanda kullanarak tensegrity’yi oluşturdu.

Snelson daha sonra bu tarz yapıların yalnızca insan yapımı nesnelerde mümkün olduğunu düşünmekte idi. Ancak Fuller, aynı sistemin doğada sık biçimde kullanıldığını düşünüyordu.
Gerçekten de, birçok gergin kasları, bağları ve tendonları ile vücudun sert kemiklerini yukarı çeken, böylece onları yerçekimi kuvvetine karşı stabilize eden ve destekleyen insan vücudu, iş başındaki benzer fiziksel kuvvetlerin en iyi örneğidir. Son birkaç on yılda bilim insanları, gerilimin organlar, dokular, hücreler ve hatta moleküller düzeyinde işleyen doğanın temel bir tasarım ilkesi olduğunu da göstermiştir.
Hatta aslında bakarsanız insan vücudunun tahmin bile edemeyeceğiniz yapılar ile bağlantısı açığa çıkarılmıştır. Bir örneğini bu yazımızda bulacaksınız. Kemiklerinizin ile Eyfel Kulesinin Ortak Paydası Matematiktir!
Tensegrity Nedir? Bu Yapılar Nasıl Ayakta Duruyor?
Konu hakkında bu kısa bilgilendirmenin ardından, bu denge fikrinin yüzen masa ile nasıl çalıştığını görelim. Öncelikle aşağıdaki basitleştirilmiş bir diyagramı inceleyelim.
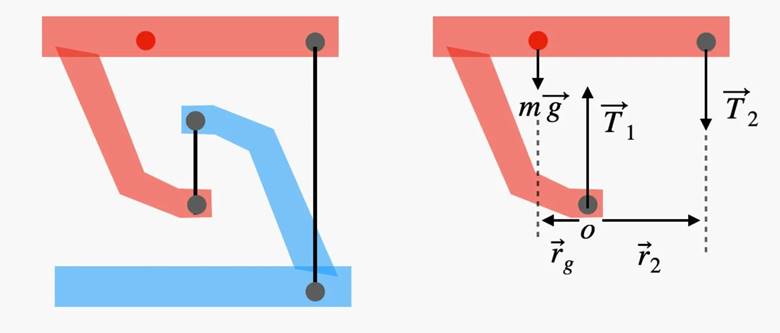
Yukarıdaki görselde masaya etki eden üç kuvvet görebilirsiniz. Birincisi aşağı doğru çeken yerçekimi kuvvetidir (mg). Yerçekimi kuvveti masanın tüm parçalarıyla etkileşime girse de, bu, ağırlık merkezinde bulunan tek bir kuvvete eşdeğerdir.
Bir sonraki kuvvet T1 olarak etiketlenmiştir. Bu, mavi kısımdan başlayan ve yukarı doğru olan çekmenin sonucu oluşan bir gerilim kuvvetidir. Son olarak, T2 olarak adlandırılan başka bir gerilim vardır. Ancak bu aşağıya doğrudur.
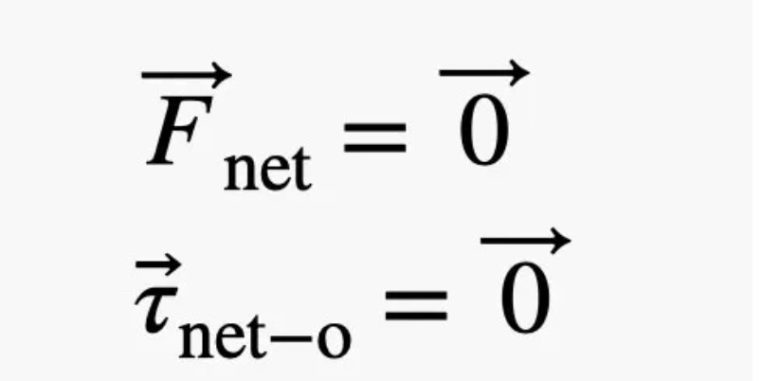
Eğer bir cisim hareketsiz ise (yani ivmelenmiyorsa), onun bir denge durumunda olduğunu söyleriz. Bu, aşağıdaki iki koşulun doğru olması gerektiği anlamına gelir. İlk denklem, nesne üzerindeki toplam kuvvetin (Fnet) sıfır vektörüne eşit olması gerektiğini söylüyor. İkinci denklem ise, istediğiniz herhangi bir nokta etrafındaki toplam torkun (τ net ) sıfır olması gerektiğini söyler.
Tork kavramı biraz karışıktır, bu yazıda fazla detayına girmeyeceğiz. Ancak bunu bir “bükülme” kuvveti olarak düşünebilirsiniz. Basit bir örnek için aşağıdaki görsel göz atınız. Bir torkun değeri, uygulanan kuvvetin büyüklüğüne ve uygulandığı yere bağlıdır. Bir nesne dengedeyse, saat yönündeki döndürme torklarının toplamı, saat yönünün tersine olan torklara eşit olmalıdır.
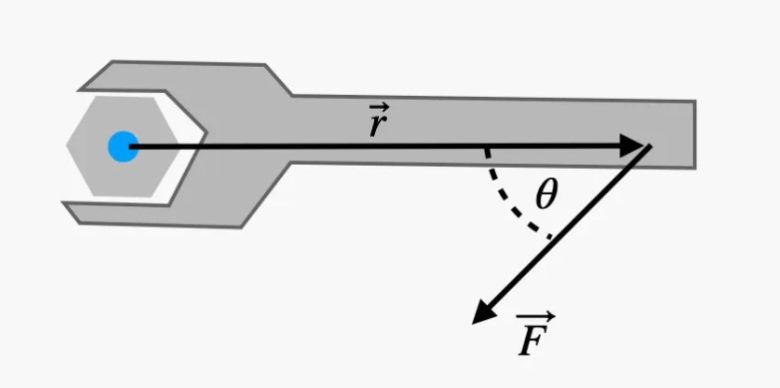
Burada F uygulanan kuvvet, r dönme eksenine olan uzaklık ve θ döndürme açısıdır. Tork formülü ise 𝜏 = 𝐹 r sinθ biçimindedir. Ancak dümdüz aşağı çekerseniz, sin 90° = 1 olur ve bu τ = Fr biçiminde sadeleşir.
Havada Asılı Duran Bir Masada Tüm Bu Kuvvetler Nasıl Çalışıyor?
Şimdi yüzen masamıza geri dönelim. Sonuçta bu masanın sabit durmasını istiyoruz. Bu nedenle de etki eden tüm kuvvetler aşağıdaki denklemi sağlamalıdır. Bu üç kuvvetin tümü dikey (y) yönde olduğundan, yatay (x) boyutunu göz ardı edebiliriz. Bu sayede işler kolaylaşacaktır.
Aşağıdaki denklem bizlere, yukarı çekme geriliminin iki aşağı kuvvete (yerçekimi ve diğer gerilim) eşit olması gerektiğini söyler. Ama tork için bir açıklama yapmaz.
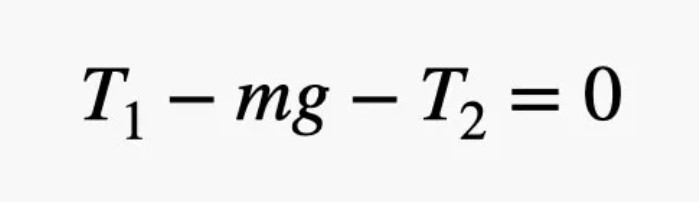
Torku hesaplamak için nesne üzerindeki herhangi bir noktayı seçebilirsiniz. Yukarı doğru çeken ipin bağlı olduğu o noktasını seçelim. Saat yönündeki torkların negatif değerler olduğunu ve saat yönünün tersinin pozitif olduğunu kabul edelim. Her bir kuvvetten kaynaklanan torku elde etmek için τ = Fr olduğunu unutmayın. Ancak T1 için mesafe (r) sıfır olduğundan, bu gerilim sıfır tork ile sonuçlanır.

Bu durumda, diğer iki kuvvetle, torklarının dengelenmesinin tek yolu, birinin saat yönünde, diğerinin ise saat yönünün tersine çekmesidir. T2 sağ taraftan aşağı çekmektedir. Bu da T2 r2 ‘nin o noktası etrafında negatif bir tork oluşturması anlamına gelecektir.
Ancak yerçekimi kuvveti de aşağı çeker. Bu da üst platformun ağırlık merkezinin, merkezi destek dizisinin diğer tarafında olması gerektiği anlamına gelir. Aslında işin püf noktası da budur.
Sonuç Olarak;
Basit bir örnek üzerinden Tensegrity sistemlerinin ara planındaki fiziksel süreçleri anlatmayı çalıştık. Elbette bu tarz sistemleri büyük ölçekte inşa etmek istediğimiz zaman işin içine karmaşık başka hesaplamalar da karışacaktır. Ancak hepsinde işin özü bir biçimde dengeyi sağlamaktır.

Günümüzde yapılan en güncel Tensegrity sistemlerden biri Avustralya’da yapılan Kurilpa köprüsüdür. Köprü Brisbana kentinde, Brisbane nehri üzerinde yer almaktadır. Bu köprü Cox Rayner Mimarlık ve Arup Mühendislik tarafından tasarlanmış ve Baulderstone şirketi tarafından uygulaması yapılmıştır. Köprünün toplam uzunluğu 470 m, genişliği 6.5 m olup en büyük açıklık 120 m’dir.
Kaynaklar ve ileri okumalar
- Wait a Second, That Table Has No Legs! Yayınlanma tarihi: 25 Nisan 2020; Bağlantı: https://www.wired.com/s
- 8 Incredible Structures Around the World That Use Tensegrity to Defy Gravity. Yayınlanma tarihi: 2 Ocak 2021; Bağlantı: https://mymodernmet.com/tensegrity-architecture/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel