Geometrideki en nefis ilişkilerden biri, bir şeyin şeklinden bağımsız olarak ilişki doğru kaldığında oluşur. Sonuçta telefonda bir arkadaşınıza geometri sorusu sorduğunuzu ve ne çizmesi gerektiğini anlattığınızı düşünelim. Bunun sonucunda doğal olarak telefon hattının diğer ucundaki kişinin talimatlara göre çizdiği şekil kişiden kişiye değişecektir.
Ancak bir parçası kimi durumlarda her zaman aynı kalır. Buna geometri de değişmez denir. Böyle bir durum bize, Matematik Koleksiyonu (Synagoge) adlı kitabında İskenderiyeli Pappus (yaklaşık M.Ö 300-350) tarafından gösterilmiştir;
Bir çiftçi, her sırada üç ağaç olacak biçimde on düz sıra oluşturacak şekilde dokuz ağaç dikmek istesin. Bunu nasıl yapabilirdi? Bu amaca ulaşmanın ilginç bir yolu Pappus teoremi kullanmaktır. İskenderiyeli Pappus ( 290-350) antik çağın son büyük Yunan matematikçilerinden biridir. İskenderiye’de geometri dersleri vermiş, çok sayıda öğrenci yetiştirmiştir. Az önce bahsettiğimiz eseri, eski dönem matematikçilerinin çalışmalarının günümüze aktarıldığı en ünlü eserdir.
Bu eserin birinci cildi aritmetik konusunda kaleme alınmıştır. İkinci cildi sürekli çarpımlarla ilgili bir sistem geliştirilmesini anlatmaktadır. Eserin üçüncü cildi düzlem ve uzay geometrisi problemlerine ayrılırken, dördüncü ciltte üç çembere teğet olacak şekilde çizilen dış çemberle ilgili teoremler yer almaktadır.
Eserin beşinci cildi şekillerin alan ve hacimlerini konu alır. Altıncı cilt hakkında bilgi sahibi değiliz. Yedinci cilt eski matematikçilerin adlarını ve çalışmalarını içermektedir. Sekizinci cildinde ise mekanik konuları incelenmiştir.
Pappus yaşadığı dönemdeki matematiksel gerilemenin farkındaydı. Bu eserini de bu düşüşü durdurmak için kaleme almış, ancak başarılı olamamıştı. Bu nedenle Pappus’un eseri Yunan-Roma matematiğinin ulaştığı en yüksek noktadır.
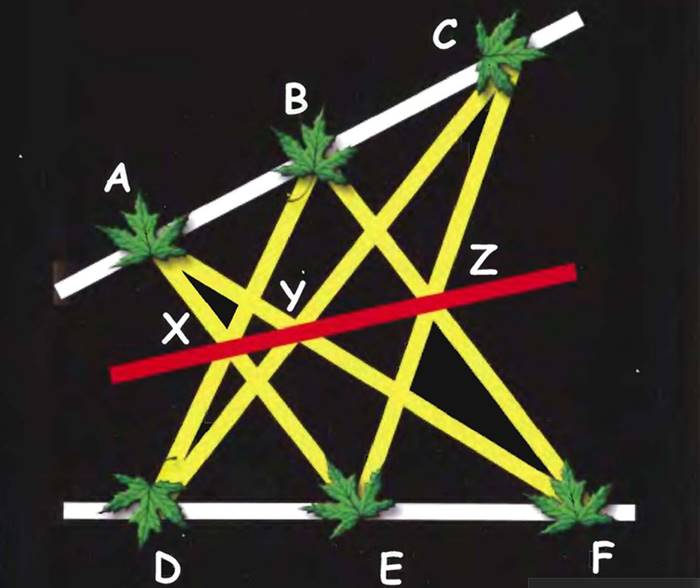
Pappus Teoremi Nedir?
En başından beri geometri ölçüler yani uzunluklar, alan ve hacim hesaplamaları ile ilgiliydi. Ancak Pappus teoremi bu anlamda farklıydı. Bu teorem tüm ölçüm öğelerinden bağımsız olarak kurgulanan ilk teoremdi. Sinagog, 1588’de Latince çevirisinin yapılmasından sonra Avrupa’da yaygın olarak tanınmaya başlandı. Kitap devamında Isaac Newton ve Rene Descartes’ın ilgisini çekti. Pappus’un Sinagog’u yazmasından yaklaşık 1300 yıl sonra, Fransız matematikçi Blaise Pascal, Pappus teoreminin ilginç bir genellemesini sağladı.
İki nokta her zaman bir doğru üzerinde bulunur. Ama üç noktanın aynı doğru üzerinde bulunması geometride önemli bir şeydir. Keza iki doğrunun bir noktada kesişmesinde şaşılacak pek bir şey yoktur. Ama üç doğrunun aynı noktada kesişmesi kayda değer bir durumdur. Pappus Teoreminde de üç noktanın aynı doğru üzerinde denk gelmesini ispatlayarak bu estetik zevki derinlemesine hissedeceğiz.
Ama öncesinde ispatta kullanacağımız Menelaus teoreminden bahsetmeliyiz. Bu bize üç noktanın doğrusal olup olmadığını garanti eden bir teoremidir. Detayları burada: Küresel Üçgeni Bize Tanıtan İskenderiyeli Menelaus Ve Ünlü Teoremi
Menelaus Teoremi:

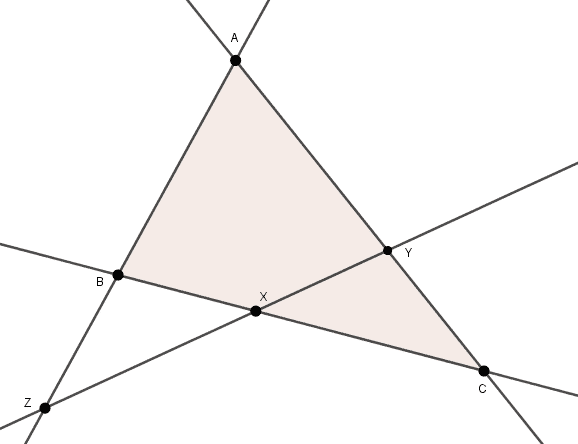
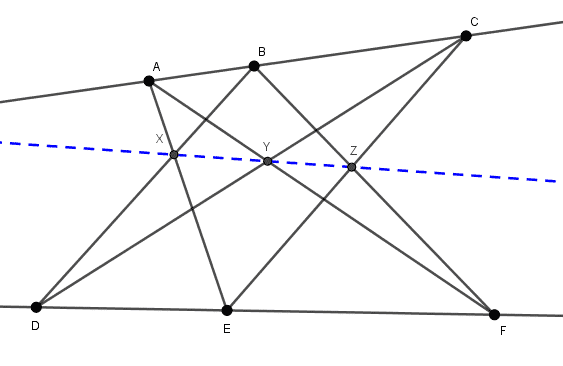
Pappus Teoreminin İspatı
Şekil 2 de, UVW üçgeninde birtakım Menelaus teoremleri uygulayacağız. UVW üçgeni ile sırasıyla EC, AF, DB, DF ve AC doğrularını göz önüne alarak Menelaus yapalım. Sonrada bulduğumuz sonuçların hepsini taraf tarafa çarpalım. Bu durumda ZV/ZW . YW/YU . XU/XV çarpımı 1 olacaktır. Bu da X, Y, Z noktalarının doğrudaş olduğunu gösterir.
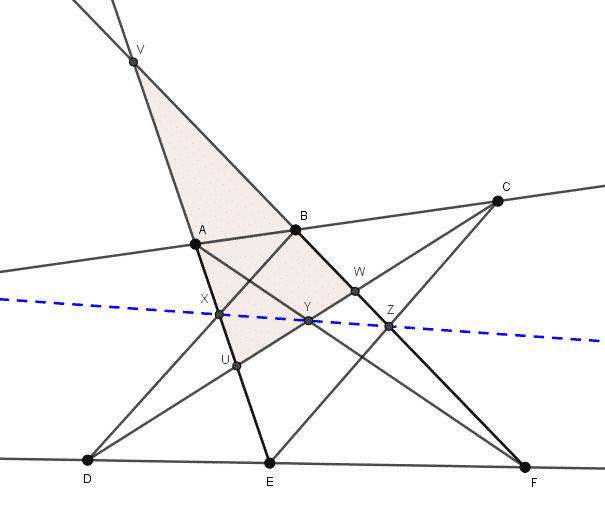
Pappus Teoremi gibi açılardan, uzunluklardan bağımsız bir şekilde noktaların bir doğru üzerinde olup olmaması gibi durumlarla ilgilenen geometrinin bir kolu olan Projektif (izdüşümsel) geometri içerisinde bu teoremin ispatı çok daha kolaydır. Ayrıca göz atmak isterseniz: Dört Renk Teoremi Matematiği Nasıl Değiştirdi?
Kaynakça:
- Davis, P.J., Hersh, R. (2015). Tüm Yönleriyle Matematiksel Deneyim içinde (sayfa 188). (Çev: Soner Durmuş, Oben Eruçar). Nobel Yaşam
- Clifford A. Pickover; The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics; ISBN: 9781402788291
Matematiksel