İskenderiyeli Menelaus, küresel bir üçgeni (bir kürenin yüzeyinde üç büyük dairenin oluşturduğu bir üçgen) ilk kez tasarlayan ve tanımlayan Yunan matematikçi ve astronomdur. Kendisinin matematik tarihine önemli katkıları olmasına rağmen bir çok kişi onun adını muhtemelen sadece Menelaus teoremi ile duymuştur. Ezberleyip geçtiğimiz bu teoremin arkasındaki hikayeyi de muhtemel merak etmemiştir.
ciltlik bir eseri vardır. Bu eserde, küresel üçgenlerin tanımlar ve düzlem ve küresel üçgenlere ilişkin teoremini
tanıtır.
İskenderiyeli Menelaus’un MS birinci yüzyılın sonlarında Roma’da yaşadığını biliyoruz. Batlamyus bize orada bazı gözlemler yaptığını söylüyor, ancak kendisi aslında bildiğimiz tek şey bu. Ne yazık ki yaşamı hakkında başka bir detay mevcut değildir.
Ayrıca yazılarının bir kaç parçası dışında neredeyse tümü kayıptır. Neyse ki günümüze küresel trigonometrinin temellerini konu alan Sphaerica (Küreler) adlı eserinin orjinali olmasa bile Arapça ve Latince çevirileri kalmıştır. Menelaus’un en önemli yapıtı olan, altı ciltlik bu eser Arapçaya Sabit bin Kurra tarafından çevrilmiştir. Menelaus bu eserinde Öklid’in düzlemsel üçgenleri ele almasına benzer şekilde küresel üçgenleri incelemiştir.
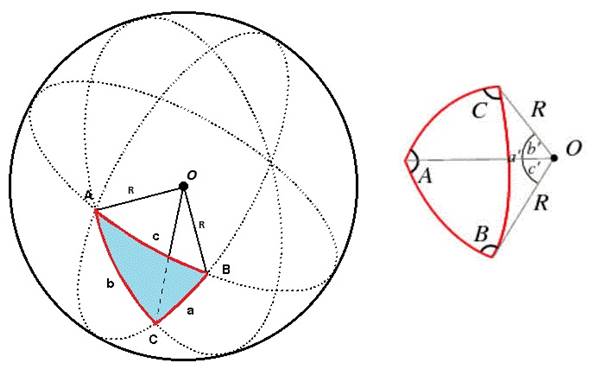
Bu çalışması küresel trigonometri adına önemli bir dönüm noktasıdır. Kitabın ikinci bölümü astronomiye küresel geometrinin uygulanması konusuna ayrılmıştır. Kitabın üçüncü ve son bölümü ise küresel trigonometri hakkındadır ve Menelaus’un kendi adıyla anılan ve bir çoğumuzun lise yıllarından tanıdığı Menelaus teoremi de bu bölüm de yer almaktadır. Bu çalışma 16. yüzyılda matematikçi Francesco Maurolico tarafından Yunancaya çevrilmiştir.
Ayrıca Menelaus, küresel üçgenlerin iç açılarının toplamının, doğrusal üçgenlerden farklı olarak, 180 dereceden büyük, küçük ve eşit olabileceğini belirten ve bunun kanıtını veren ilk bilim insanıdır.
Menelaus Teoremi Nedir?
Aslında ondan önce de birkaç yüzyıl boyunca bilim insanları bir kürenin geometrisini araştırmışlardı. Ancak ilgileri aslında temel olarak matematikseldi. Astronomi arka planda yer alıyordu. Bu çalışmaların hepsi elbette önemliydi. Yayların genel özelliklerini tanımladılar ve bazı yayların diğerlerinden daha uzun olduğunu gösterdiler, ancak hiçbir şeyin uzunluğunu hesaplamadılar. Bunun nedeni elbette trigonometrik kuralların henüz belirlenmemiş olması idi. Ama Menelaus tüm bunları değiştirdi.
Bu teoreme göre bir üçgenin iki kenarını ve üçüncü kenarının uzantısını kesen bir doğrunun kenarlar üzerinde oluşturduğu altı doğru parçasından birbirine komşu olmayan üçünün çarpımı, öteki üç doğru parçasının çarpımına eşittir. ( İspatı için kaynaklar kısmına göz atabilirsiniz). Bu teoremin küresel trigonometride ve astronomik uygulamalarda ve hesaplamalar da çok önemli bir yeri vardır.
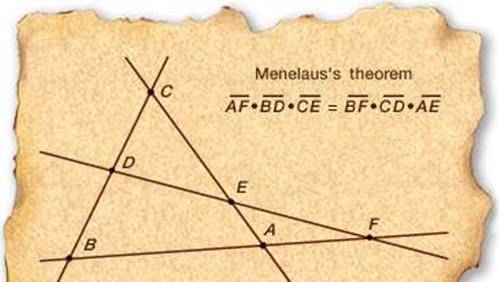
Bu kitabından başka Menelaus’un çemberde kiriş ve geometri hakkında da kitapları olduğu bilinmektedir, ancak bu kitaplar günümüze ulaşmamıştır. Günümüzde adı geometri kitaplarının yanı sıra bir kraterde yaşamaktadır.
Kaynaklar ve İleri Okumalar:
- Britannica, The Editors of Encyclopaedia. “Menelaus of Alexandria”. Encyclopedia Britannica, 26 Mar. 2024, https://www.britannica.com/biography/Menelaus-of-Alexandria. Accessed 22 May 2024.
- Menelaus teoremi ispatı; https://tr.wikipedia.org/wiki/Menelaus_teoremi
- Murdin, P.. (2000). Menelaus of Alexandria (c. 70-c. 130). Encyclopedia of Astronomy and Astrophysics. 10.1888/0333750888/3851.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






