Kökleri antik tarihe uzanan klasik bir matematiksel ve algoritmik bulmaca olan Josephus Problemi, problem çözme becerilerimizi zorluyor. Problem adını tarih alanında önemli bir çalışmalar imza atan Titus Flavius Josephus’tan (MS 36-100) alıyor. Josephus problemi MS 1. yüzyılda yaşandığı rivayet edilen kanlı bir olaya bağlanır.

Flavius Josephus, Kudüs aristokrasisinin bir üyesi olarak, MS 64 yılında, çeşitli nedenlerden dolayı rehin alınan bazı Yahudi rahiplerinin serbest bırakılması için Roma İmparatoru Neron (MS 54-68) ile görüşmek üzere Roma’ya gitmişti. Bu sırada Neron da Yahudi ayaklanmasının bastırılması için general Vespasian’ı görevlendirmiştir. Neticede Vespasian’ın emrindeki askerler Flavius Josephus ve 40 arkadaşını bir dağ kasabası olan Jotapata’da kuşatma altına almış ve hepsi bir mağarada mahsur kalmıştı.
Josephus Problemi Nedir?
Hikâyeye göre, bu 40 kişi Roma’nın köleleri olmaktansa, topluca intihar etmeye karar verirler. Ancak bunu belli bir sıra ile yapmayı planlarlar. Bunun için Flavius ve arkadaşları bir çember oluşturacak biçimde dizilirler. Plana göre belli bir yönde hareket edilecek ve her üç kişiden biri öldürülecektir. Yani birinciden başlayarak 3’e kadar sayıp 3’üncü kişinin öldürülmesini, daha sonra 4’ten başlayarak üçe kadar sayıp
6’ıncının öldürülmesi ve buna sadece iki kişi kalıncaya kadar devam edilmesi planlanır.
Efsaneye göre Flavius Josephus matematiksel becerileri sayesinde bu ölümcül şans oyununda hayatta kalmayı başaracaktır. Bunu kendisinden önce ölecek son kişinin konumunu hesaplayarak başarır. Sadece o ve onu öldürecek kişi hayatta kaldığında da, kurbanını Romalılara teslim olmaya ikna eder. Peki ama Josephus nerede durmuştur?

Bu problem yıllardan beri matematikçilerin, bilgisayar bilimcilerinin ve bulmaca meraklılarının zihnini meşgul etti. Aslında problem aldatıcı derecede basitti. Problemi şu biçimde de düşünebilirsiniz. Toplamda bir çemberin etrafında bulunan ve n kişiden oluşan bir ortamda, yalnızca bir kişi kalana kadar her k. kişi eleniyor. Yapılması gereken ise o son kişinin konumunu bulmaktır.
Şimdi Josephus problemini iki kişiden birinin elendiği n kişi arasında oynanan bir oyun olarak ele alalım. Yani 1’den n’ye kadar numaralandırılmış n kişi sırayla (1, 2, 3, …, n) bir çember etrafında sıralanıyorlar. 1 numaralı kişiden başlayıp belli bir yön takip edilerek sayılıyor, her iki kişiden biri eleniyor. Bu şekilde n–1 kişi eleninceye dek devam ediliyor. Oyunu kazanan oyuncunun numarası kaçtır?
Josephus Problemi Nasıl Çözülmelidir?
Aslında problemin çözümüne geçmeden önce daha kolay anlaşılması için 41 kişi yerine 8 kişi ile bu soruyu çözmeye çalışalım. Her iki kişiden birinin öldüğünü, diğer bir deyişe herkesin yanında sağ kalan kişiyi öldürdüğünü kabul ediyoruz.
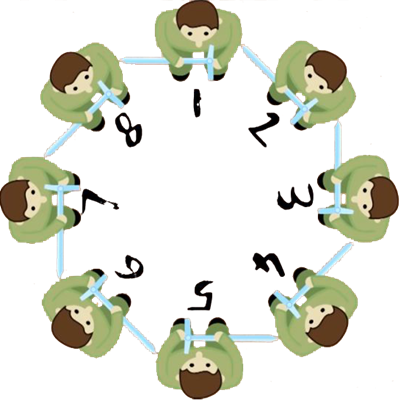
Bu durumda 1 numaralı kişi 2. kişiyi, 3 numaralı kişi 4. kişiyi, 5 numaralı kişi 6. kişiyi ve 7 numaralı kişi 8. kişiyi öldürecek. Şu an geriye 1,3,5 ve 7 numaralı kişiler kaldı.
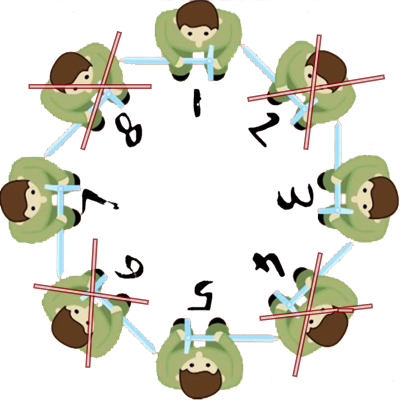
Aslında bu noktadan sonra görsele bakarak çözümü görmüş olmanız gerekiyor. Sonucunda şu an 1 numaralı kişi 3. kişiyi öldürdü, 5 numaralı kişide 7. kişiyi öldürdü ve geriye sadece 1 ile 5 kaldı. Bu durumda Josephus 1 numarada durmalı ve 5 numaralı kişiyi ikna etmeli, olmadı öldürmelidir. Şimdi daha genel bir kural bulmaya çalışalım. n sayma sayısı için oyunu kazanan kişinin numarasını J(n) ile gösterelim. Oyuncu sayısını çift ve tek olarak iki ayrı durumda inceleyeceğiz.
Çift Sayıda Asker Varsa
Eğer oyun 2n kişiyle başlarsa ilk turun sonunda çember etrafında sadece tek numaralı oyuncular kalacaktır. Geriye kalan kişi sayısı ilk kişi sayısının yarısı kadar olacaktır. Ancak artık sıralamaları değişmiş durumdadır. Dikkat ederseniz önceden 3 numaralı olan kişi artık 2. konumda, 5 numaralı kişi 3. konumda, 7 numaralı kişi 4. durumda durmaktadır.
Yani aslında yeni yerleri ilk konumlarının bir fazlasının yarısı kadardır. Diğer bir deyişle eski konumları yeni konumlarının iki katının bir eksisi kadardır. Bu durumda J(n) kazanan oyuncunun numarası olduğundan, n≥1 için J(2n)=2J(n)-1 eşitliğini yazabiliriz.
Tek Sayıda Asker Varsa
Şimdi de oyunun 2n+1 yani tek sayıda kişiyle oynandığını varsayalım. Bu durumda, ilk turun sonunda sırasıyla 2,4,6,… ,2n ölecek ve geriye bu sefer tek numaralı kişiler kalacaktır. Yani ikinci turda 1 numaralı kişi aslında 3. kişi, 2 numaralı kişi aslında 5 kişi, 3 numaralı kişi 7. kişi oldu.
Bu durumda kişilerin yeni konumlarını bulmak için eski konumlarını 2 ile çarpıp bir toplamamız gerekiyor. Buradan da, J(n) kazanan oyuncunun numarası olduğundan, n≥1 için J(2n+1)=2J(n)+1 eşitliğini yazarız. Sonrasında da bu iki bilginin bir araya getirilmesi ile de ispatımızı yapıp genel çözümü elde edebiliriz.
Josephus Problemin Cevabı
Şimdi bir tablo yapalım. Aşağıdaki tablo 15 kişiye kadar hayatta kalan kişinin durması gereken yeri gösteriyor. 8 kişi için 1 cevabını yukarıda bulmuştuk. Diğerleri için de çemberler çizerek gerekli sağlamayı yapabilirsiniz.
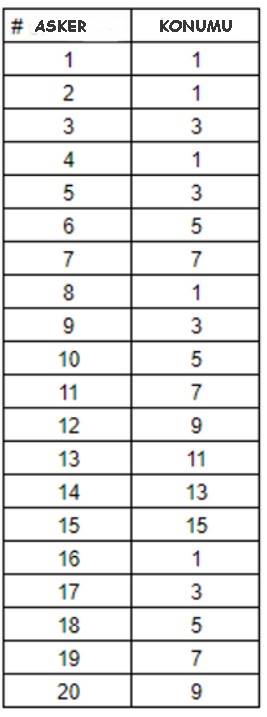
Yukarıdaki tabloda dikkat etmeniz gereken şey hayatta kalanların her zaman tek numaralı konumlarda bulunduğudur. Ayrıca bu tek sayıların belli bir noktaya kadar ikişer arttığını sonra da yine 1’e geri döndüğünü görebilirsiniz. Aslında tabloya dikkatle bakarsanız 1 numaralı konumda hayatta kalanların karşısında 2 sayısının kuvvetlerinin yer aldığını fark edeceksiniz. Yani elimizde 32 askerimiz olduğu zamanlarda da 1 numaralı asker hayatta kalan olacaktır.
Başlangıçtaki problemimizde 41 kişi vardı. 41 sayısına en yakın 2’nin kuvveti 32dir. Sonrasında sayarak çözümü elde edebiliriz. 33. asker 3, 34. asker 5, 35. asker 7, 36. asker 9, 37. asker 11, 38. asker 13, 39. asker 15, 40. asker 17 ve 41. asker 19. konumda durursa hayatta kalacaktır. Bu durumda da Josephus son kalan olmak için 19. konumda bulunmalıdır. Yazının bitiminde ayrıca göz atmak isterseniz: Sahte Para Bulmacası İle Matematiksel Gerçekliği Arayalım
Kaynaklar ve ileri okumalar
- Solve This Deadly Puzzle! Investigating the Josephus Problem. yayınlanma tarihi: 2 Haziran 2020; Bağlantı: https://www.gleammath.com
- The Josephus Problem – Numberphile. Yayınlanma tarihi: 28 Ekim 2016; Bağlantı: https://www.youtube.com
- The Josephus Problem: https://en.wikipedia.org/wiki/Josephus_problem
- Park, Jang-Woo & DOGAN, Ali & Teixeira, Ricardo. (2021). Block Josephus Problem: When the Reality is More Cruel Than the Old Story. Hacettepe Journal of Mathematics and Statistics. 50. 1-12. 10.15672/hujms.750167.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










