Denklem çözme konusunda zorluk yaşamıyor olabilirsiniz. Ancak emin olun, karşınıza çıktığında nasıl çözüleceğini tahmin edemeyeceğiniz birçok denklem vardır. Aslında, bilim insanlarının karşılaştığı denklemlerin büyük bir kısmı da bu türden karmaşık denklemlerdir. Bu gibi durumlarda, farklı çözüm yaklaşımlarına ihtiyaç duyulur. Bu yöntemlerden biri de “bisecting (ikiye bölme) yöntemi”dir.
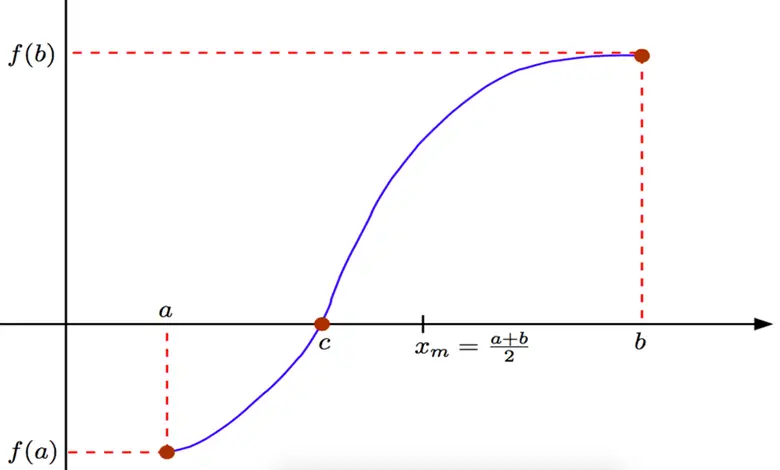
Ancak öncelikle, konuya yabancı olanlar için bazı temel bilgiler verelim. Bir denklemi çözmek, o denklemin kökünü ya da köklerini bulmak anlamına gelir. Bir denklemin kökleri, f(x)=0 denkleminin çözümleridir. Bu aynı zamanda, f(x) fonksiyonunun grafiğinin x eksenini kestiği noktalar anlamına gelir.
Eğer bir fonksiyon belirli bir aralıkta süreklilik gösteriyorsa — yani fonksiyonun grafiğini elinizi kaldırmadan çizebiliyorsanız — ve bu aralıkta fonksiyonun işareti değişiyorsa, bu fonksiyon mutlaka f(x)=0 noktasından geçiyor demektir. Bu durumda, x eksenini kestiği nokta fonksiyonun bir kökünü temsil eder.
İkiye Bölme Metodu Nedir?
Şimdi elimizde, sürekli bir fonksiyon olan f olsun. Ayrıca, bu fonksiyonun tanımlı olduğu [a,b] aralığında, f(a) ve f(b) değerlerinin zıt işaretlere sahip olduğunu da kabul edelim. Bundan sonraki adımlar oldukça basittir.
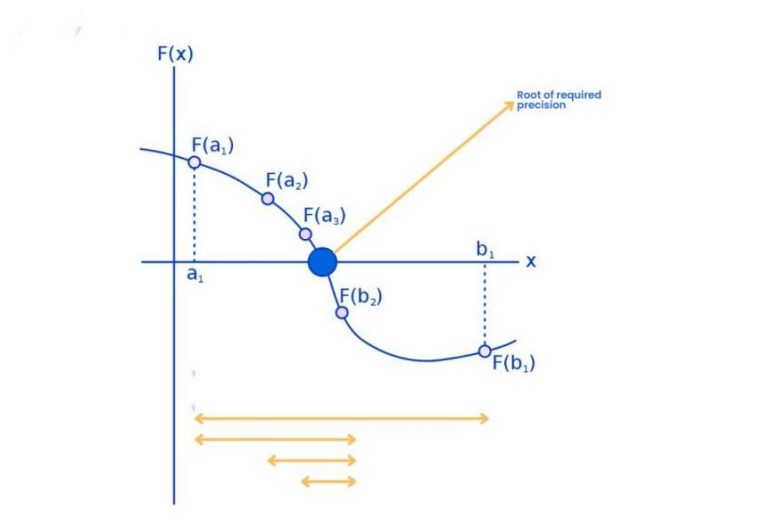
Yapmamız gereken, bu iki uç noktanın aritmetik ortalamasını almaktır. Yani a ve b değerlerini toplayıp ikiye bölerek yeni bir nokta elde ederiz. Bu noktaya c diyelim. Bu işlemin sonucunda ya f(a) ile f(c), ya da f(c) ile f(b)) zıt işaretlere sahip olacaktır.
Zıt işaretli olan çiftin bulunduğu alt aralık, kökün yer aldığı aralıktır. Bu durumda, aradığımız kökü daha hassas bir şekilde yaklaşık olarak bulmak için aynı işlemi bu yeni aralıkta tekrarlarız.
- Eğer f(a) ve f(c) zıt işaretliyse, b değeri c ile değiştirilir.
- Eğer f(b) ve f(c) zıt işaretliyse, bu kez a değeri c ile değiştirilir.
- Son olarak, eğer f(c)=0 ise, bu durumda kök tam olarak bulunmuş olur ve c değeri çözümdür.
İkiye Bölme Metodu İle İlgili Bir Örnek

Şimdi, yukarıdaki problemi ikiye bölme yöntemiyle çözmeye çalışalım. İlk olarak, a=1 ve b=2 değerlerini alıp fonksiyonda yerine koyalım. Bu durumda f(1)=−2 ve f(2)=4 sonuçlarını elde ederiz. Ayrıca, fonksiyonun sürekli olduğunu bildiğimiz için aradığımız kök, [1,2] aralığında yer almalıdır.
Şimdi 1. adım olarak a=1 ve b=2 değerlerinin ortasındaki değeri bulalım. Yani 1 ile 2’yi toplayıp sonrasında ikiye bölelim. Bu durumda ilk c değerimiz 1,5 olacaktır. Bu değeri fonksiyonda yerine yazarsak: f(1,5)=−0,125 elde ederiz. Elde edilen f(c) değeri negatif olduğu için, a değeri c ile değiştirilmelidir.
Bu işlemleri aynı mantıkla sürdürerek aşağıdaki tabloyu oluşturabiliriz. Tabloyu dikkatle incelediğinizde, 13. adımdan sonra fonksiyonun kökünün yaklaşık olarak 1,521 değerine yakınsadığını görebilirsiniz. Dolayısıyla, bu yönteme göre fonksiyonun kökü yaklaşık olarak 1,521 civarındadır.
| Adım Sayısı | a | b | c | f(c) |
| 1 | 1 | 2 | 1,5 | −0.125 |
| 2 | 1,5 | 2 | 1,75 | 1.6093750 |
| 3 | 1,5 | 1,75 | 1.625 | 0.6660156 |
| 4 | 1,5 | 1.625 | 1.5625 | 0.2521973 |
| 5 | 1,5 | 1.5625 | 1.5312500 | 0.0591125 |
| 6 | 1,5 | 1.5312500 | 1.5156250 | −0.0340538 |
| 7 | 1.5156250 | 1.5312500 | 1.5234375 | 0.0122504 |
| 8 | 1.5156250 | 1.5234375 | 1.5195313 | −0.0109712 |
| 9 | 1.5195313 | 1.5234375 | 1.5214844 | 0.0006222 |
| 10 | 1.5195313 | 1.5214844 | 1.5205078 | −0.0051789 |
| 11 | 1.5205078 | 1.5214844 | 1.5209961 | −0.0022794 |
| 12 | 1.5209961 | 1.5214844 | 1.5212402 | −0.0008289 |
| 13 | 1.5212402 | 1.5214844 | 1.5213623 | −0.0001034 |
| 14 | 1.5213623 | 1.5214844 | 1.5214233 | 0.0002594 |
| 15 | 1.5213623 | 1.5214233 | 1.5213928 | 0.0000780 |
İkiye Bölme Metodu Ne Zaman Kullanılmalıdır?
Yukarıda kısaca açıklamaya çalıştığımız yöntemin bazı avantajları ve dezavantajları vardır. Öncelikle, ikiye bölme yöntemiyle bir denklemin kökünü yaklaşık olarak bulmak mümkündür; ancak daha hassas bir sonuca ulaşmak istiyorsak işlemi birçok kez tekrarlamamız gerekir. (Bu işlemi bir bilgisayar gerçekleştirdiğinde, tekrarların fazlalığı önemli bir sorun oluşturmaz.)
Bu yöntemin en önemli avantajlarından biri, belirli koşullar sağlandığında fonksiyonun mutlaka bir değere yakınsamasının garanti edilmesidir.
Öte yandan, bu yöntem her fonksiyonda uygulanamaz. Özellikle sürekli olmayan fonksiyonlarda ikiye bölme yöntemini kullanmak mümkün değildir. Bununla birlikte, olası hataları kontrol etmek mümkündür ve bu yöntemi algoritmik bir yapıya dönüştürmek oldukça kolaydır.
Bu nedenlerle, ikiye bölme yöntemi günümüzde hesaplamalı bilimlerde yaygın olarak kullanılmaktadır. Siz de denemek isteyebilirsiniz.
Yazının devamında ayrıca göz atmak isterseniz. Matematik İspatlarıyla Bilgisayar Programlarını Birleştiren Derin Bağlantı: Curry-Howard Yazışması Nedir?
Kaynaklar ve ileri okumalar
- Rivaie, Mohd & Fakhri, Muhammad & Hayati, Nujma & Ramli, Nurul & Jusoh, Ibrahim. (2017). The n-th section method: A modification of Bisection. Malaysian Journal of Fundamental and Applied Sciences. 13. 10.11113/mjfas.v0n0.577.
- Wikipedia contributors. (2025, October 31). Bisection method. In Wikipedia, The Free Encyclopedia. Retrieved 10:32, November 5, 2025, from https://en.wikipedia.org/w/index.php?title=Bisection_method&oldid=1319728336
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel