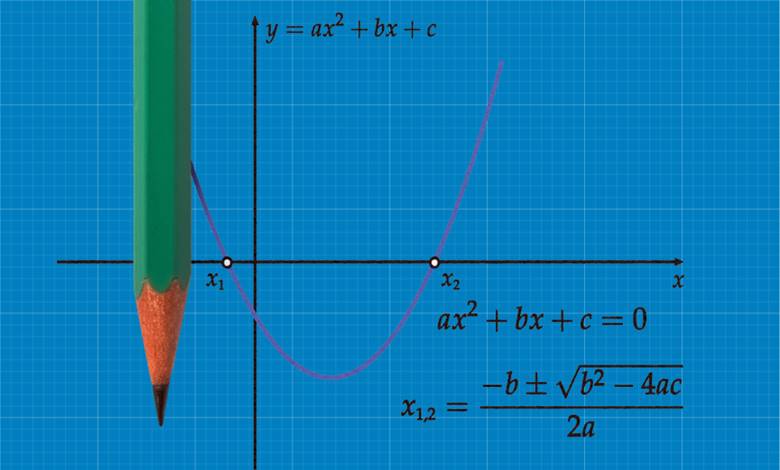
Okullarda ikinci dereceden denklemler konusunu öğrenir sonrasında da konuyu derinlemesine pek düşünmeyiz. Oysa ikinci dereceden denklemler sandığımızdan çok daha fazla yerde karşımıza çıkar. Bu yazıda ana başlıklar halinde ikinci dereceden denklemlerin 101 olmasa bile bir çok kullanım yeri hakkında fikir edinelim.
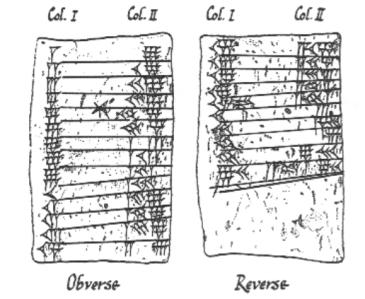
Ancak öncelikle kendileri ile nasıl tanıştığımıza bakalım. Aslında her şey M. Ö. 3000 civarında Babilliler ile başladı. Bildiğiniz gibi matematik ile ilgili bir çok kavramın kökenini araştırdığımıza karşımıza onların adı çıkar. Babilli bir çiftçi olduğunuzu varsayalım. Çiftliğinizin bir yerinde kare şeklinde üzerinde mısır yetiştirdiğiniz bir tarlanız olsun. Bu tarlada ne kadar ürün yetiştirebilirsiniz? Tarlanın bir kenar uzunluğunu iki kat büyütürseniz önceki yetiştirdiğinizin dört katı kadar mısır yetiştirebilirsiniz. Bunun sebebi yetiştirebileceğiniz mısır miktarının tarlanın alanıyla ve dolayısıyla bir kenarının karesiyle orantılı olmasıdır.
Matematiksek olarak bunu ifade edelim. Tarlanın bir kenar uzunluğu x birim olsun. Kenar uzunluğu 1 birim olan kare biçimindeki bir tarlada yetiştireceğiniz mısır miktarı ise m olsun. Son olarak c yetiştireceğiniz toplam mısır miktarı ise, bu c=m.x2 biçiminde yazılacaktır.
Yani sonuç ikinci dereceden bir denklemdir. İkinci derece denklemler ve alan hesabı öz kardeş gibidir. Vergi memuru gelip de çiftçiye neşe içerisinde “Çiftliğine ait vergi borcunu ödemek için bana c miktar mısır vermeni istiyorum” dediği an çiftçinin ikilemi başlar. “Bu miktarda mısır üretmek için ne kadar büyüklükte bir tarlaya ihtiyacı vardır?” Bu soruya kolaylıkla cevap verebiliriz. Çiftçinin ihtiyaç duyduğu tarlanın bir kenar uzunluğu x= √c/m biçiminde olacaktır.
İkinci Dereceden Denklem Çözümü İçin Farklı Bir Yaklaşım
Hesap makinesi kullanarak karekök hesabı yapmak bizim için kolaydır. Ancak, bu iş Babilliler için o kadar da kolay değildi. Babilliler bunun için modern bilgisayarlar tarafından ikinci dereceden denklemlerden çok daha zor denklemleri çözmeye yarayan bir algoritmayla (bu algoritma Newton-Raphson yöntemi ) tamamen aynı olan bir ardışık yaklaşım yöntemi geliştirdiler.
Yukarıda bahsi geçen tarla kare biçimde bir tarla olsa da, bütün tarlaların kare şeklinde olmasını bekleyemeyiz. Şimdi çiftçinin aşağıda gösterildiği gibi iki üçgene bölünebilen daha garip şekilli bir tarlaya sahip olduğunu varsayalım:
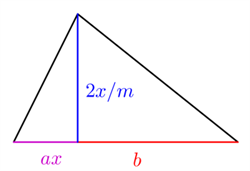
a ve b nin uygun değerleri için çiftçinin bu tarlada yetiştireceği mısır miktarı c= ax2+bx denklemi ile bulunacaktır. Bu denklemin çözümünü bulmak çok daha zordur. Fakat yine de Babilliler bir sonuca ulaşmıştır. Öncelikle bu denklemin her tarafı a ile bölünür ve tam kareye tamamlanır. Ortaya çıkan denklemin her iki tarafın karesi alınır ve meşhur eşitlik elde edilir.
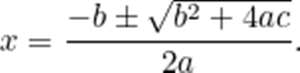
Karekök alma işleminin pozitif ve negatif olmak üzere iki sonuç verir. Bu da ikinci dereceden denklemlerin iki tane çözümü olması sonucunu doğurur. İkinci dereceden denklemlerle ilgili öğretilenler genellikle geldiğimiz bu noktada durur ve daha ileriye gitmez. Çünkü çözümü veren formüle ulaşılmıştır. Formülü bulduktan sonra, formülün ne anlama geldiğini, bize evren hakkında ne söylediğini ve bir formüle sahip olmanın gerçekten önemli olup olmadığını sorgulamalıyız. Şimdi bu formülün bizi nereye götüreceğini görelim.
Bir sürpriz, biraz matematiksel origami ve orantı duygusu
Şimdi zamanı bin yıl kadar ileri sarıp, Antik Yunanlıların ikinci derece denklemleri nasıl kullandıklarına bakalım. Yunanlılar mükemmel matematikçilerdi ve bugün hala kullandığımız matematiğin çoğunu keşfetmişlerdi. Çözmekle ilgilendikleri denklemlerden birisi basit x2=2 ikinci dereceden denklemiydi. Bu denklemin bir çözümü olduğunu biliyorlardı. Gerçekten, bu denklemin çözümü bir birim uzunlukta kenarlara sahip dik açılı bir üçgenin hipotenüsüdür.

a ve b uzunluklu dik kenarlara sahip üçgenin hipotenüs uzunluğu c ise o halde Pisagor teoreminden a2+b2=c2 yazılabilir. Bu denklemde a=b=1 ve x=c alınırsa x²=2 ve dolayısıyla x= √2 olur. Peki bu durumda x nedir? Veya soruyu Yunanlıların sorduğu gibi sorarsak, x ne tür bir sayıdır?
Yunanlılar her sayının birbiriyle orantılı olduğuna ve a ve b tam sayılar olmak üzere, tüm sayıların a/b biçiminde kesirlerle ifade edilebileceğine inanıyorlardı. Fakat, x= √2 sürpriz bir biçimde kesirlerle ifade edilemiyordu. Aslında √2 tanımlanan ilk irrasyonel sayıydı. Bu sayılarla ilgili olumlu bir düşünce tarzına sahip olmamız on dokuzuncu yüzyılı buldu. Yunanlılar bu noktadan sonra cebirden vazgeçtiler ve geometriye yöneldiler.
İkinci Dereceden Denklemler ve A4 Kağıdı
Aslında x= √2 düzenli olarak karşılaştığımız bir sayıdır. Mesela A4 boyutunda bir kağıdı her kullandığımızda x= √2 sayısına rastlarız. A0 bir metrekare alana sahip en büyük boyutlu kağıttır. A boyutlarının arasında özel bir ilişki vardır. Şimdi biraz origami yapalım. A1 boyutunda bir kağıdı alıp uzun kenarı boyunca ikiye katlarsak A2 boyutunda bir kağıt elde ederiz. A2 boyutundaki bu kağıdı tekrar ikiye katlamak bize A3 boyutunda bir kağıt verir. A3 boyutundaki kağıdı ikiye katlamak A4 boyutunda bir kağıt verir. Fakat, bu kağıtlar her birindeki A boyutların oranı aynı olacak biçimde tasarlanmıştır. Yani her bir kağıt aynı şekle sahiptir.
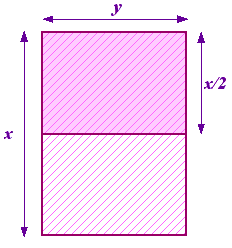
Peki, bu oran nedir? x uzun kenar olmak üzere, x ve y kenar ölçülerine sahip bir kağıt parçası ile işe başlayalım. Şimdi bu kağıdı uzun kenar y ve kısa kenar x/2 olacak biçimde iki eşit parçaya bölelim. İşe başladığımız ilk kağıdın kenarları oranı x/y ve ikinci kağıdın kenarları oranı ise y/(x/2) veya 2y/x olur. Bu iki oranın birbirine eşit olmasını istiyoruz. Eşitleyip gerekli düzenlemeleri yaparsanız elde edeceğiniz sonuç x/y= √2 olacaktır. ABD’de kullanılan ve foolscap olarak isimlendirilen kağıt farklı bir orana sahiptir. Neden böyle olduğunu görmek için tekrar Yunanlılara dönelim. Başka bir ikinci dereceden denklem ele alalım.
Altın Dikdörtgen
Bir dikdörtgenle işe başlayalım ve sonra bu dikdörtgenden dikdörtgenin kısa kenarıyla aynı ölçülere sahip bir kareyi çıkaralım. Eğer dikdörtgenin uzun kenarı 1 ve kısa kenarı x uzunluğuna sahipse, karenin kenar uzunluğu x olacaktır ve bu kareyi dikdörtgenden çıkarmak uzun kenarı x, kısa kenarı 1-x olan başka bir dikdörtgen verecektir.
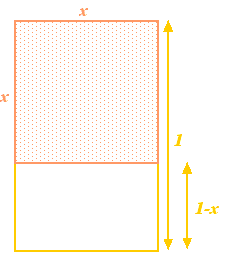
Yunanlılar, yukarıda bahsedilen büyük ve küçük dikdörtgenler aynı kenar oranlarına sahip olduğu zaman büyük dikdörtgenin en estetik dikdörtgen olduğuna inanır ve bu dikdörtgeni altın dikdörtgen olarak isimlendirirdi. Bir dikdörtgenin altın dikdörtgen olması için aşağıdaki eşitliklerinin sağlanması gerekir.
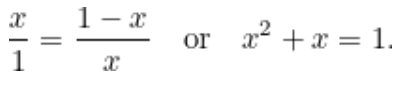
Bu ise her türlü uygulamada sıkça karşılaşılan çok önemli başka bir ikinci dereceden denklemdir. Bu denklemin (pozitif) çözümü bizi altın orana götürür. Ayrıca. x2+x+1 ikinci dereceden denklemi ayrıca tavşan popülasyonu ile ilgili çalışmalarda ve ayçiçeği tohumları ve bitki saplarındaki yaprakların yerleşimindeki örüntülerde de ortaya çıkar. Bunların hepsi, Fibonacci dizisi ile bağlantılıdır: 1,1,2,3,5,8,13,21,34… Bu dizideki her terimin bir sonraki terimle oranı gittikçe altın oranına yaklaşır.

Konikler ve ikinci dereceden denklemler
Bir el fenerini duvar gibi düz bir yüzeye doğru tutup hareket ettirirseniz bu hareket esnasında oluşan çeşitli şekiller görürsünüz. Bu şekillere konik kesitler denir ve bunlar koniden çeşitli açılarda aldığınız dilimlerle elde ettiğiniz eğrilerdir. Tam olarak bu eğriler Yunanlılar tarafından incelenmiştir ve Yunanlılar temelde dört tip konik kesit olduğunu fark etmişlerdir. Koni boyunca yatay bir kesit alırsanız bir daire, yataya küçük bir açıyla yaklaşarak bir kesit alırsanız bir elips, dikey bir kesit alırsanız bir hiperbol ve koninin bir tarafına paralel bir kesit alırsanız bir parabol elde edersiniz.
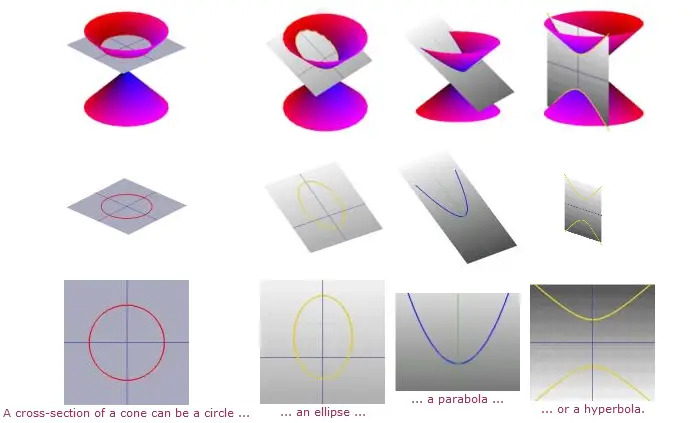
Konik kesitlerin her biri ikinci dereceden bir denklemle ifade edilir. (x,y) her bir eğrinin üzerinden alınan bir nokta olmak üzere ilgili ikinci dereceden denklemler aşağıdaki gibidir:
- Çember denklemi: x2+y2=1
- Elips denklemi: ax2+by2=1
- Hiperbol denklemi: ax2-by2=1
- Parabol denklemi: ax2=y
İlk olarak Yunanlıların incelediği eğrilere günümüzde klasik eğriler denir. Gördüğünüz bu klasik eğriler çember dışında herhangi bir pratik uygulamaya sahip değil gibi görünmektedir. Ancak bu fikir, 16. yüzyılda değişecekti.
Rönesans’ın gelmesiyle birlikte düşünürler dünyaya farklı bir gözle bakmaya başladılar. Bu kişilerden birisi de Bunlardan biri Kopernik’ti. Kopernik Güneş’i gök kürelerinin merkezine koymuş ve Evren anlayışımızı değiştirmişti. Ancak kendisi, Dünya’nın yörüngesinin bir çember biçiminde olduğunu düşündü. Kepler, Tycho Brahe’nin gözlemlerini kullanarak, Kopernik’in öngörüleri ile deneysel veriler arasında tutarsızlıklar bulana kadar bu düşünce biçimi devam etti.
İkinci Dereceden Eğriler Evreni Keşfetmemize Yaradı
Kepler’in keşfettiği şey, gezegenlerin Güneş’in etrafında daireler halinde değil, elipsler biçiminde döndükleriydi. Kepler’in kuralları daha sonra gözlemlere mükemmel bir şekilde uyum gösterdi. Konik kesitler, keşfedilmelerinden 1500 yıl sonra nihayet sahneye çıkıyorlardı.
İkinci dereceden denklemler, yalnızca gezegenlerin yörüngeleri tanımlamakla kalmadı. Aynı zamanda onları daha yakından gözlemlemenin bir yolunu da verdi. Astronomideki ilerlemelerin anahtarı teleskopun icadıydı. Galileo bir teleskop kullanarak Jüpiter’in aylarını ve Venüs’ün evrelerini gözlemledi. Galileo’nun teleskobu, kesişen iki hiperbol tarafından oluşturulan mercekler içeriyordu.
Çoğu insan Galileo’yu İspanyol Engizisyonu ile Kopernik güneş sistemi görüşünün geçerliliği üzerine girdiği savaşla tanır. Bununla birlikte kendisi hayatının çoğunu cisimlerin nasıl hareket ettiğini anlamaya adamıştır. Galileo’nun çalışmasının merkezinde, arabamızı ne zaman (ve nasıl) durduracağımız ve aynı zamanda bir golü nasıl atacağımız gibi konularla ilgisi olan ivme fikri ve ikinci dereceden denklemlerin bunda oynadığı rolün anlaşılması vardır.
Hareket ve İkinci Dereceden Denklemler
Bir cisim bir kuvvet etkisinde olmadan bir yönde hareket ediyorsa, o yönde sabit hızla hareket etmeye devam eder. Bu hıza v diyelim. Bu cisim x=0 noktasından başlar ve t süresi boyunca bu şekilde hareket ederse, sonuçtaki konumu x = v.t ile hesaplanır. Ancak ideal bir dünyada yaşamıyoruz. Bu nedenle yerçekimi, sürtünme gibi sebeplerle genelde bir kuvvet bu cisme etki eder. Bu gibi etkiler sonucunda da bir ivmelenme yaşanır.
Bu nedenle, cismin başlangıç hızı u ise, t zamanından sonraki v hızı v = u + at ile elde edilir. Buradaki a ivmeyi temsil eder. Galileo, bu ifadeden parçacığın konumunu bulabileceğimizi fark etti. Eğer parçacık x=0 konumunda başlıyorsa, o zaman t anındaki s konumu s=u.t+1/2.a.t2 denklemi ile bulunabilirdi. Bu aslında t’yi s’ye bağlayan ikinci dereceden bir denklemdir ve hepimiz için birçok önemli sonucu vardır.

Boş bir yolda araba sürerken aniden önünüze çıkan bir kedi nedeniyle durmak zorunda kaldığınızı varsayalım. Bir arabayı u hızından 0 hızına düşürmek için sabit bir yavaşlama -a uygulanırsa, t’yi çözmek ve yerine koymak durma mesafesi s’yi verir. Yani s= u2/2a. Bu sonucun aslında hayati bir önemi vardır. Hızınızı ikiye katlamanın durma mesafenizi iki katına değil dört katına çıkaracağını bize gösterir. Yani, ikinci dereceden denklemi doğru bir şekilde çözmek, sizin veya bir başkasının hayatını kurtarır.
Balistik ve Parabol
Zamanı mesafeyle ilişkilendiren basit ikinci dereceden formül, nesnelerin yerçekimi altında nasıl hareket ettiğini inceleyen balistik biliminin de temelidir. Balistik veya atış bilimi, mermi ve füzelerin hareketlerini inceleyen bir bilim dalıdır. Uygulamalı mekaniğin bir kolu olarak düşünülebilir. Bu durumda bir cisim y yönünde sabit g ivmesi ile düşer.
Buna karşılık, sabit bir hızla (hava direncinin yokluğunda) yatay olarak x yönünde hareket eder. Bu durumda eğer x = y = 0 noktasında x yönünde u hızı ve yukarıya doğru v hızı ile harekete başlarsa, Galileo t zamanındaki konumun x=u.t ve y= vt-1/2.gt2 şeklinde olduğunu gösterdi. Bu denklem sisteminin çözümü de bize yeni bir ikinci dereceden denklem verecektir. Dikkat çekici olan, yörüngenin ortaya çıkan şeklinin bir parabol olmasıdır.

1600 civarında, Galileo Pisa’da bir kilise ayinine katıldı. Belki de biraz sıkıldığından bir avizenin ileri geri sallanışını izlemeye başladı. Bu sayede de dikkate değer bir keşif yaptı: avizeyi sallamak için geçen süre, genliğinden bağımsızdı. Bu keşif sarkacın ve devamında çeşitli saatlerin icadına yol açtı. Ancak Galileo gözlemi hakkında yeterli açıklama yapamadı. Bunu yapmak için başka bir ikinci dereceden denkleme ihtiyacımız vardı.
Newton ve İkinci Dereceden Denklemler
Newton, Galileo’nun öldüğü yılda doğdu. Galileo ve Kepler’in çalışmalarından ilham aldı. Bu bilimsel devler, dinamik ve gök mekaniği fenomenlerini doğru bir şekilde tanımlamışlardı. Ama hiçbiri bilimsel açıklamalar formüle etmemişti. Gözlemledikleri fenomenlerin matematiksel açıklamasını sağlamak Newton’a kaldı. İlk olarak, Galileo’nun gözlemlerini açıklayan üç hareket yasasını formüle etti. İkinci olarak, temel yerçekimi yasasını tanımladı. Buna göre, iki kütle, aralarındaki uzaklığın karesi ile ters orantılı bir kuvvet tarafından birbirini çekiyordu.
Newton ayrıca optik alanında da çalıştı. Bunun sonucunda Galileo’nun kullandığı teleskop lenslerinin, farklı renklerdeki ışığı farklı şekillerde kırarak sorunlara yol açtığını fark etti. Aynaya dayalı bir teleskop tasarlayarak bunun üstesinden geldi. Bu aynanın ideal şekli de parabol olmalıydı.
Newton bu açıklamalarının yanında kalkülüsü geliştirmekle de meşguldü. Kalkülüs, onun hareket yasalarına göre hareket eden nesneleri tanımlamak için mükemmeldi. Kalkülüsün elindeki en temel araç ise diferansiyel denklemlerdi.
Diferansiyel denklemlerin uygulama alanları sınırsızdır ve modern teknolojinin çoğunda hayati bir rol oynar. Galileo’ nun fark ettiği bir sarkacın hareketi de bir diferansiyel denklem olarak tanımlanır. Sarkacın küçük salınımları durumunda bu denklem salınım zamanını bulmak için çözülebilir. Bunu çözmek de, ikinci dereceden bir denklemin çözümünü bulmayı gerektirir!
İkinci Dereceden Denklemler ve Akışkanlar Dinamiği
İkinci dereceden denklemler ve ikinci dereceden diferansiyel denklemler arasındaki bağlantı tesadüf değildir. İkisi de Newton’un ikinci yasasında tanımlanan kuvvet ve ivme arasındaki ilişki ile bağlantılıdır. Newton bu yasayı formüle ederken esas olarak katı cisimlerin hareketini düşünüyordu. Ancak kısa süre sonra aynı yasaların su ve hava gibi akışkanların hareket tarzına da uygulanabileceği anlaşıldı.
Özellikle, bir akışkanın hızı ile basıncı arasındaki ilişkileri bulmak için Newton yasalarını kullanmak mümkündür. Bu yasaların gelişmiş versiyonları Navier-Stokes diferansiyel denklemleri olarak adlandırılır. Bununla birlikte, birçok sıvı akışı türü için geçerli olan belirli bir çözüm, uçakları mümkün kılmıştır. Bu Bernouilli denklemi adı verilen ikinci dereceden bir denklemle bağlantılıdır.
İkinci dereceden eğriler ve denklemlerin birçok uygulaması olduğunu ve insanlık tarihinde temel bir rol oynadığını gösterdik. Ancak daha sayı 101’e ulaşmadı. Devamını da başka yazıya saklayalım. Ayrıca göz atmak isterseniz: İkinci Dereceden Denklemleri Çözmenin Modern Bir Yolu
Kaynak ve İleri Okuma: 101 uses of a quadratic equation; https://plus.maths.org/
Matematiksel











matematiğin anlaşılmayan değil, doğru yoldan öğrenilmeyen bir yürüyüş olduğunu ne güzel göstermişsiniz. emeğinize sağlık.