Cebir nedir? Geleneksel olarak nasıl öğretildiği göz önüne alındığında, konuyu bilmeyenler için bu sorunun cevabı x, y, z, a, b ve c ile bazı üst simgelerden bir alfabe çorbası biçiminde olacaktır. Ancak cebirin problemli olması için hiçbir neden yoktur. Cebir sadece bildiklerimizi kullanarak gizli bilgileri ortaya çıkarma sanatıdır.
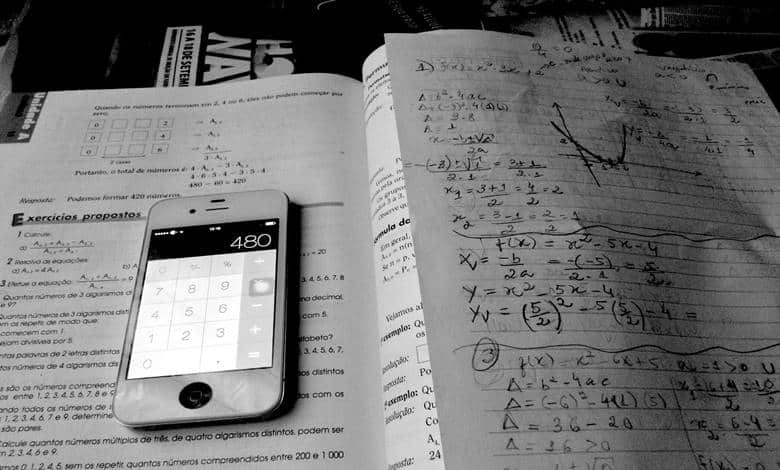
Cebirin adı Muhammed el-Harezmi’nin (780-850) 9. yüzyılda kaleme aldığı; Mısır, Babil, Yunan, Çin ve Hint matematiğinde bilinmeyen sayıları bulma konusundaki fikirleri derlediği, kitabının başlığındaki el-cebr kelimesinden gelmektedir.
El-Harizmi kitabında bize ax2 + bx = c gibi temel cebirsel denklemleri çözmek için reçetelerden bahseder. Bu arada 14 farklı türdeki ‘kübik’ denklemi çözmek için geometrik yöntemler verir. Ancak hatırlatalım. Tarihin bu noktasında x ya da üslü sayılar gibi kavramlar bildiğimiz anlamda mevcut değildi.

Bu nedenle Harizmi’nin yazdıklarında herhangi bir denklem günümüzde gördüklerimize pek de benzemiyordu. Aslına bakarsanız cebir bir problemi ortaya koymak ve çözümü açıklamak için karmaşık kelimelerden oluşan bir sanattı.
Onun düşünce mantığını kavramak için bir örnek üzerinden gidelim. Denklemimiz x2+10x=39 olsun. Bu denklem Harezmi tarafından bu denklemi “Hangi sayının karesi, sayının 10 katı ile toplanırsa 39 eder?” biçiminde ifade edilmekteydi. Burada x2 terimi kenar uzunluğu x olan bir kareyi temsil eder. Denklemdeki +10x terimi ise kenar uzunluğunun 10 katının, karenin alanına eklendiğini gösterir. Denklemin sağındaki 39 sayısı, toplam alanın değeridir.
İkinci Dereceden Denklemler Bugünkü Haline Nasıl Geldi?
Cebir problemleri 16. yüzyıla kadar kelimeler yardımı ile çözülmeye devam etti. Cebiri kelimelerden uzaklaştırma girişimi François Viète ile başladı. Hesaplamalarına sesli ve sessiz harfleri dahil etti ve sonucunda da A3 + B2A = B2Z gibilerinden bir denklemi ifade etmek için “A cubus + B quad. in A, æquetur B quad. in Z” biçiminde bir şeyler yazacaktı. Yazdıkları bugünkü denklemlere hiç benzemese de yine de önemli bir adımdı.
Bu arada araya küçük bir not düşelim. Yukarıdaki ifade de artı işareti olmasına rağmen eşittir işaretinin olmadığına dikkat edin. Bunun nedeni o dönemlerde eşittir işaretinin henüz bilinmiyor olmasıydı. Eşittir işareti hayatımıza Robert Recorde tarafından aşağı gördüğünüz çalışması ile dahil oldu.

Gördüğünüz gibi ikinci dereceden denklemlerin bugün tanıdığımız formuna erişebilmesi için uzun bir yoldan geçmesi gerekiyordu. Günümüzde ikinci dereden denklem dediğimiz zaman her lise öğrencisinin hatırlayacağı formül aşağıdaki gibidir. Peki bu formül hayatımıza nasıl girdi? Bunu anlamak için Babil matematiğine ve vergi hesaplamalarına geri dönmeniz gerekecektir.
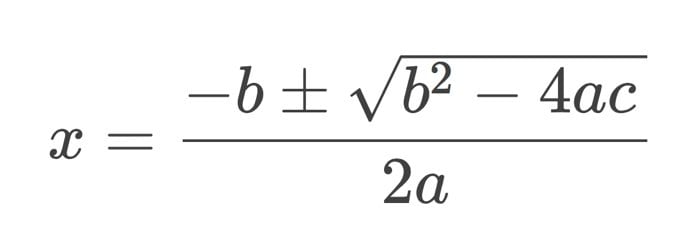
“Alanı 60 olan bir dikdörtgenin uzunluğu, genişliğinden 7 kat fazladır. Genişliği nedir?” Günümüzde bir ilk öğretim sorusu gibi görünen bu ve buna benzer denklemler antik Babil tableti YBC 6967’de karşımıza çıkıyor. Babilliler bunu cebir ve geometri arasındaki yakın bağlantıyı gösteren bir dizi adımla çözeceklerdi. Günümüzde bu işleme tam kareye tamamlama diyoruz.
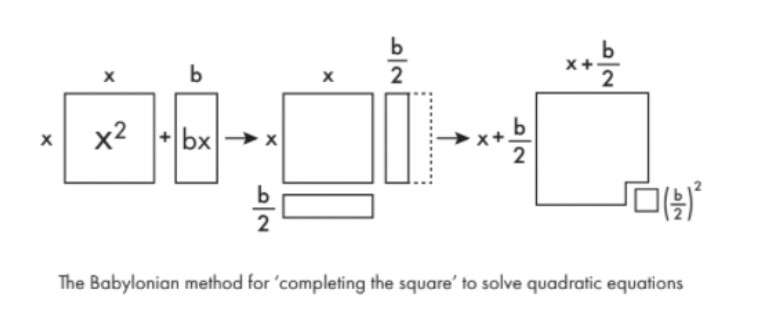
Burada x 2 kenarı x olan bir kare ve bx , uzunluğu x ve genişliği b olan bir dikdörtgendir. Bu dikdörtgeni uzunlamasına ikiye bölün ve yarısını orijinal karenin altına ekleyin. Böylece daha büyük bir kare elde edersiniz. Ancak eklediğiniz küçük karenin alanını yani ( b /2) 2′ni daha sonrasında bulduğunuz sonuçtan çıkarmanız gerekecektir. Bu durumda cevabınızın ( x + b /2) 2 – ( b /2) 2′ ye eşdeğer olduğunu görebilirsiniz. Okullarda öğrendiğiniz ikinci derece denklemler bu hesaplamanın yeniden düzenlenmesinin bir sonucudur.
İkinci Dereceden Denklemleri Çözmek İçin Modern Yöntem
İkinci dereden denklemler faydalı araçlardır. Ancak günümüzde hiçbirimiz hesaplamalarımızı Babil’ler gibi yapmadığımız için, çözümü yapabilmek için bazı formüllerin ezberlenmesi gerekecektir. Geçtiğimiz yıllarda Pittsburgh’daki Carnegie Mellon Üniversitesi’nde bir matematikçi olan Po-Shen Loh ikinci derecen bir denklemi çözmek için yeni bir yöntem önerdi. Bu yöntem ezberlenmesi gereken tanımları da ortadan kaldırıyor.
Tanımları vermeden direk bir örnek üzerinde açıklamamızı yapalım. Sorumuz “x2 – 2x+4=0 denkleminin köklerini bulunuz.” biçiminde olsun.
Geleneksel yöntem, A, B ve C değerlerini hesaplamak için bunları formülde yerlerine yerleştirmektir. Fakat Loh’un yaklaşımı soruyu sezgisel olarak çözüyor. Toplamları 2, çarpımları 4 olan iki sayıya ihtiyacımız var. İlk iş 2 sayısının ortalamasını alalım. -2 ve 4 sayısını toplar ve ikiye bölersek ortalamalarını 1 buluruz. Bu sayı aslında aradığımız iki kökün ortasındaki sayıdır.
Bu durumda köklerimiz (1-z) ve (1+z) dir. ( Burada z herhangi bir harftir.) Bu kökleri birbiri ile çarparsak 1-z2 = 4 sonucunu elde ederiz. Bu denklemi düzenlersek z2 =-3 olacaktır. Sonucunda bu durumda aradığımız kökler aşağıdaki biçimde olacaktır.
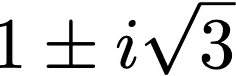
İyi ama ikinci dereden denklemlerin ne işe yaradığını anlatmadınız derseniz, onları da bu yazımızda bulabilirsiniz. İkinci Dereceden Denklemlerin 101 Kullanım Yeri
Kaynaklar ve ileri okumalar
- Loh, Po-Shen. (2019). A Simple Proof of the Quadratic Formula.Bağlantı: https://doi.org/10.48550/arXiv.1910.06709
- How the quadratic formula evolved, from Babylon to modern math class. Yayınlanma tarihi: Bağlantı: How the quadratic formula evolved, from Babylon to modern math class
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









