Pizza dilimini katlayarak yemek neden işe yarar? Bir peygamberdevesi karidesinin yumruğu nasıl Pringles cipsiyle açıklanır? Şaşırtıcı bir biçimde, eğrilik ile dayanıklılık arasında güçlü bir geometrik bağ vardır.

Hepimiz bu durumla karşılaşmışızdır: Elinize bir dilim pizza alırsınız, tam ısıracakken dilim aşağı doğru sarkar ve parmaklarınızdan çaresizce düşecek gibi olur. Hamur, üzerindeki malzemelerin ağırlığını taşıyacak kadar sert değildir. Belki de daha az malzeme seçmeliydiniz. Ama üzülmeye gerek yok; yılların pizza yeme tecrübesi bu soruna pratik bir çözüm getirdi: Dilimi U şekline getirip katlamak.
Pizza dilimini katladığınızda dilim artık sarkmaz, düzgünce elinizde kalır ve afiyetle yemeye devam edersiniz. Yanınızda pizza yoksa, aynı deneyi bir kâğıt parçasıyla da kolayca yapabilirsiniz.
Bu pizza hilesinin arkasında, eğri yüzeylerle ilgili son derece güçlü bir matematiksel sonuç yatar. Öyle şaşırtıcıdır ki, onu keşfeden matematik dehası Carl Friedrich Gauss, bu buluşa Theorema Egregium adını vermiştir; Latince’de “olağanüstü” ya da “dikkate değer teorem” anlamına gelir.
Düz bir yüzeyi yuvarlak bir yüzeye dönüştürmek ya da yuvarlak bir yüzeyi düzleştirmek hiç de kolay değildir. Hatta imkânsıza yakındır. Denemek isterseniz, bir portakalın etrafına bir kâğıt sarmaya çalışın. Ne yaparsanız yapın, sonunda kırışıklıklar ve kıvrımlar ortaya çıkar.
Tersi de geçerlidir. Portakalın kabuğunu soyup düzleştirmeye çalışın. Kabuğu kesmeden bunu başaramazsınız. Peki, yuvarlak ve düz yüzeylerin birbirine dönüşmesini engelleyen şey nedir? Matematikçiler bu durumu Gauss eğriliği kavramıyla açıklar.

Gauss Eğrileri Nedir?
Bir kâğıt alın ve onu bir silindir hâline getirin. İlk bakışta kâğıdın düz, silindirin ise eğri olduğunu düşünürsünüz. Ama Gauss meseleyi farklı ele aldı. O, bir yüzeyin eğriliğini yüzey büküldüğünde değişmeyecek bir biçimde tanımlamak istiyordu.
Silindirin üzerinde yaşayan bir karıncayı hayal edin. Karınca pek çok farklı yol seçebilir. Yüzey boyunca kıvrılıp bir daire çizebilir, düz bir çizgide yürüyebilir ya da ikisinin arasında bir yol izleyip helis oluşturabilir. Gauss’un dahice buluşu, bir yüzeyin eğriliğini karıncanın seçebileceği tüm yolları dikkate alacak şekilde tanımlamaktı.
Herhangi bir noktadan başlayın ve karıncanın izleyebileceği en uç iki yolu bulun: en içbükey ve en dışbükey olanı. Sonra bu yolların eğriliklerini çarpın. (Eğrilik, içbükey yollar için pozitif, düz yollar için sıfır, dışbükey yollar için negatiftir.) İşte bu işlemin sonucunda çıkan sayı, Gauss’un o noktadaki eğrilik tanımıdır.
Birkaç örnek deneyelim. Silindirin üzerindeki karınca için iki uç yol vardır: eğri, daire biçimli yol ve düz bir yol. Düz yolun eğriliği sıfır olduğu için, bu iki eğriliği çarptığınızda sonuç sıfır çıkar. Matematikçilerin deyimiyle, bir silindir aslında düzdür — yani Gauss eğriliği sıfırdır. Bu da, bir kâğıt parçasını rulo yaparak silindir elde edebilmemizi açıklar.
Peki ya karınca bir kürenin üzerinde yaşasaydı? Bu kez hiçbir düz yol bulamazdı. Tüm yollar aynı miktarda kıvrılır ve bu nedenle Gauss eğriliği pozitif bir sayı olur. İşte bu nedenle bir kağıt parçasını asla bir küre haline kesmeden getirmezsiniz. İşte bu fikir, bizim de evrenin dışına çıkmadan evrenin eğriliğini anlayabilmemizi sağlar. Bildiğimiz kadarıyla evren düzdür.
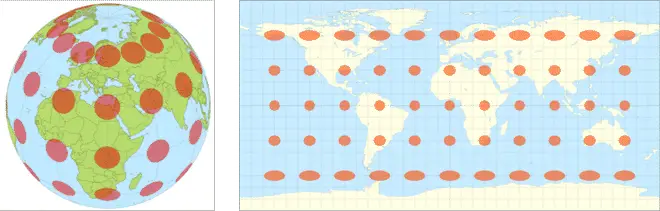
Gauss eğriliği nedeniyle bir haritayı kağıt üzerinde doğru bir şekilde çizmek imkansızdır. Görmeye alışkın olduğunuz dünya haritası, açıları doğru şekilde gösterir, ancak alanları büyük ölçüde bozar. Bir küre üzerine çizilen eşit büyüklükteki daireler, bir haritada çarpıtılmış olarak gözlemlenir.
Gauss Eğrileri ile Pizzanın Ne Alakası Var?
Pizza dilimi masadayken düzdür, yani Gauss eğriliği sıfırdır. (Dilimin yüzeyinde yürüyen bir karıncanın alabileceği tüm olası yollar düzdür.) Gauss’un teoremi bize şunu söyler: Bir yüzeyi bükseniz bile, onun en az bir yönü düz kalmak zorundadır. Pizza için de durum aynıdır.
Dilimi elinize aldığınızda aşağı doğru sarkmasının nedeni, düz yönün yana dönmesidir. Bu, yemeği zorlaştırır. Dilimi yanlamasına katladığınızda ise düz yön ağzınıza doğru çevrilir. Böylece dilim sertleşir ve kolayca yenir. İşte pizza dilimini katlamanın matematiksel açıklaması budur.

Şimdi elinize aldığınız pizza dilimini tekrar inceleyin. Bir yandan diğer yana giden yol düz iken ( görselde kırmızı), kabuktan uca giden yolun eğimli olduğuna ( görselde siyah) dikkat edin. İlk görseldeki pizzayı malzemeleri dökmeden yemek mümkün değildir. Ancak pizza diliminin ortasından bastırarak yanları içe doğru katlarsanız düzlüğün yönünü değiştirir ve yemeye uygun hale getirirsiniz.
Bir kâğıdı tek yönde büktüğünüzde, diğer yönde otomatik olarak sertleşir. Bu fikri bir kez kavradığınızda, doğada ve insan yapılarında sık sık karşınıza çıkar. Örneğin bir çime yakından bakın. Çoğu kez ortasındaki damar boyunca katlanmıştır. Bu kat, yaprağa ekstra dayanıklılık kazandırır ve yaprağın sarkmasını engeller.
Eğrilik Güç Demektir
Mühendisler de aynı prensibi kullanır. Eğrilik, yapılara dayanıklılık kazandırır. Madrid’deki Zarzuela hipodromunda İspanyol mühendis Eduardo Torroja, stadyumdan dışarı doğru uzanan çok ince bir beton çatı tasarladı. Çatı yalnızca birkaç santimetre kalınlığında olmasına rağmen geniş bir alanı kaplar, çünkü eğrilik ona sağlamlık kazandırır.

Eğrilik, yapıları güçlü kılar. Boş bir gazoz kutusunun üzerine çıktığınızda, kutu incecik duvarlarına rağmen rahatlıkla ağırlığınızı taşır. Oysa kutunun kenarı, bir kâğıt yaprağı kadar incedir. Onu bu kadar sağlam yapan şey, yüzeyindeki eğriliktir.
Eğrilikle sağlanan dayanıklılığın en sıradan örneklerinden biri, her yerde karşımıza çıkan oluklu yapı malzemeleridir. Örneğin, bir oluklu karton kutuyu düşünün. Kıvrımlar estetik amaçla değildir. Malzemeyi hem ince ve hafif tutarken hem de büyük yükler altında eğilmeyecek kadar sağlam hâle getirmek amacı taşır. Oluklu metal levhalar da aynı mantıkla çalışır.
Oluklu malzemeler ya da gazoz kutuları oldukça sağlamdır, ama malzemeleri daha da güçlü kılmanın bir yolu vardır. Bunu kendiniz denemek için buzdolabına gidin ve bir yumurta alın. Yumurtayı avucunuzun içine yerleştirin, parmaklarınızı etrafına sarın ve sıkın. (Denemeden önce yüzüğünüzü çıkarmayı unutmayın.) Dayanıklılığına şaşıracaksınız.
İki Yönde Eğrilik Daha Çok Güç Anlamına Gelir
Gazoz kutuları ve oluklu metal levhalar bir yönde eğridir ama diğer yönde düzdür. Bu eğrilik onlara belli bir dayanıklılık kazandırır, fakat sonuçta hâlâ üretildikleri düz levhalara geri döndürülebilirler.

Buna karşılık yumurta kabukları her iki yönde de eğrilidir. İşte yumurtanın gücünün sırrı budur. Matematik diliyle söylersek, bu çift eğrili yüzeylerin Gauss eğriliği sıfır değildir. Böyle yüzeyler yırtılmadan ya da gerilmeden düzleştirilemez. Gauss’un teoremi bize bunu garanti eder.
Nükleer santrallerin soğutma kulelerinin ikonik şekli de her iki yönde eğriliği kullanır. Bu şekle hiperboloid denir ve yapıyı inşa etmek için gereken malzeme miktarını en aza indirir. Normal bacalar güçlüdürler ama kolayca bükülüp çökmeye yatkındırlar. Hiperboloid biçimindeki bir baca ise her iki yönde de eğriliğe sahip olduğu için bu sorunu çözer. Çift eğrilik yapıyı kilitler ve sıradan bacalarda olmayan ekstra bir sağlamlık kazandırır.
Çift eğrilikten güç alan bir başka şekil de Pringles cipsidir. Matematikçilerin deyimiyle bu şekle hiperbolik paraboloid denir. Pringles’ın şeklinden gelen bu dayanıklılığı, İspanyol-Meksikalı mimar ve mühendis Félix Candela çok iyi anlamıştı. Bu özel şekli kullanarak betonun ne kadar ince ve zarif olabileceğini gösteren dev yapılar inşa etti.

Peki Pringles’ın şeklini bu kadar güçlü yapan şey nedir? Bunun nedeni, basınç ve gerilmeyi dengeleme biçimidir. Her yapı ağırlığı taşımak ve sonunda bu yükü yere aktarmak zorundadır. Bunu iki yolla yapar:
Birincisi basınçtır; ağırlık nesneyi içe doğru sıkar. İkincisi gerilmedir; burada ağırlık nesnenin uçlarını dışa doğru çeker ve onu esnetir. Hiperbolik paraboloid bu iki dünyanın en iyi özelliklerini bir araya getirir.
İçbükey U şeklindeki kısımlar gerilme ile esner, dışbükey kemer biçimli kısımlar ise basınçla sıkışır. Çift eğrilik sayesinde bu form, itme ve çekme kuvvetleri arasında hassas bir denge kurar. Böylece ince kalmasına rağmen şaşırtıcı derecede güçlü olur.
Sonuç Olarak
Eğrilikten gelen dayanıklılık fikri dünyamızı şekillendiriyor ve kökleri geometrinin derinliklerine uzanıyor. Bu yüzden bir dahaki sefere elinize bir pizza dilimi aldığınızda, etrafınıza bakın ve bu basit pizza hilesinin arkasında yatan büyük mirası hatırlayın.
Gauss ile adı anılan ilginç bir başka teorimi de bu yazımızdan okuyabilirsiniz: Gauss Ayakkabı Bağcığı Yöntemi İle Alan Hesaplamasını Öğrenelim!
Kaynak: How a 19th Century Math Genius Taught Us the Best Way to Hold a Pizza Slice. Kaynak site: wired. Yayınlanma tarihi: How a 19th Century Math Genius Taught Us the Best Way to Hold a Pizza Slice/
Matematiksel





