Datça’ya giderseniz, Eudoxus’un doğduğu ve öldüğü yer olan Knidos antik kentine uğramadan dönmeyin. Harabeler arasında dolaşırken, günümüzden iki bin yıl öncesinde insanların ne kadar derin matematiksel çalışmalar yaptığını kendinize hatırlatın.
Knidoslu Eudoksus’un matematiksel eserlerinin tam adları günümüze ulaşmamış, diğer yazılarından ise yalnızca bazı parçalar korunabilmiştir. Buna rağmen, onun Antik Çağ’ın en önemli matematikçilerinden biri olduğu söylenebilir. (Kimilerine göre de bu kişi Arşimet’tir.) Arşimet‘e atfedilen π‘yi hesaplama yönteminin, aslında Eudoxus’a ait olduğunu söyleyenler de vardır. Bu nedenle kendisini tanımamız gerekir.
Knidos’lu Eudoxus Kimdir?
Knidos’ta doğan Eudoksus’un, matematik öğrenimine Güney İtalya’daki Yunan kolonisi Tarent’te, Pisagor’un ardıllarından Arkytas’ın yanında başladığı bilinmektedir. Sicilya’da Philiston’dan tıp eğitimi almış, Atina’da muhtemelen Platon ve Akademi’deki diğer filozofların derslerine katılmıştır.
Ardından Mısır’daki Heliopolis kentinde rahiplerden astronomik gözlem tekniklerini öğrenmiştir. Tüm bu birikimle, Marmara Denizi’nin güney kıyısındaki Kyzikos kentinde kendi okulunu kurmuş ve çevresine birçok öğrenci toplamıştır.
Yaklaşık MÖ 368 yılında Eudoksus, öğrencileriyle birlikte ikinci kez Atina’ya gider. Daha sonra doğduğu şehir olan Knidos’a, artık saygın bir yurttaş olarak geri döner ve burada bir gözlemevi kurar. Yaptığı astronomik gözlemler, Rodoslu Hipparkhos’un (MÖ 190–120) çalışmalarına temel teşkil edecek en az bir eserine kaynaklık eder. Hipparkhos bunu minnetle dile getirir.
Aristoteles’in aktardığına göre Eudoksus, gezegen hareketlerini açıklamak için bir sistem geliştirmiştir. Bu modelde, merkezde Dünya’nın bulunduğu toplam 27 küreden oluşan bir düzen vardır. Eudoksos yedi ciltten oluşan bir coğrafya eseri de kaleme almıştır. Bu çalışmasında, bilinen dünyadaki ülkeleri ve halkları tanıtır, siyasi sistemlerini açıklar ve dini inançları hakkında bilgi verir. Ne yazık ki bu eser günümüze ulaşmamıştır; ancak Antik Çağ’da yaşamış birçok yazar tarafından alıntılanmıştır.
Eudoxus’un Matematiğe Katkıları Nelerdir?
Knidoslu Eudoksos, irrasyonel sayıların ortaya çıkardığı karmaşık probleme dahiyane bir çözüm getirmiştir. MÖ 300 civarında yaşayan Öklid de bu çözümü benimseyerek Elementler adlı eserinin V. kitabında Eudoksos’un orantı kuramına yer vermiştir.
Çalışmalarından biri olan Eşit Oranlar Teorisi, oran ve orantı konusunun gelişimine katkıda bulunur. Bu teorisi Öklid’in Elementler Kitabının V. ve VI. Cildinin; diğer bir çalışması Ölçülemeyen Büyükler Teorisi (ortak bir ölçütü olmayan büyüklükler) ile de aynı kitabın X. ve XII. Cildinin temel kaynağı olur.
Eudoksos, irrasyonel büyüklüklerle başa çıkmak için oldukça açık ve etkili bir yöntem geliştirmiştir. Öncelikle oranı, büyüklük bakımından karşılaştırılabilen iki şey arasındaki ilişki olarak tanımlar. Bu ilişki, bir büyüklüğün diğerine göre ne kadar fazla olduğunu, yani onu kaç kez içerdiğini ifade eder.
Eudoksos, oranların nasıl karşılaştırılacağını açıklarken şu mantığı kullanır. İki oran, aynı kurallara göre karşılaştırıldığında hep aynı sonuca varıyorsa eşittir. Yani, birinci oran “birinci büyüklük / ikinci büyüklük”, ikinci oran da “üçüncü büyüklük / dördüncü büyüklük” olsun. Bu oranlardan alınan herhangi katlar karşılaştırıldığında, ikisinde de birinci sayı ikinci sayıdan büyükse ya da eşitse ya da küçükse, o zaman bu iki oran birbirine eşittir.
Eudoxos’un oran tanımı, bugün kullandığımız şekilde şöyle açıklanabilir: Dört büyüklük olan a, b, c ve d için, a : b oranı c : d oranına eşittir. Bu eşitlik, aşağıdaki koşullar sağlandığında geçerlidir. Herhangi iki doğal sayı m ve n seçildiğinde:
- Eğer m⋅a>n⋅b ise, m⋅c>n⋅d olmalıdır.
- Eğer m⋅a=n⋅b ise, m⋅c=n⋅d olmalıdır.
- Eğer m⋅a<n⋅b ise, m⋅c<n⋅d olmalıdır.
Bu tanım, hem rasyonel hem de irrasyonel büyüklükler için geçerli olduğu için son derece güçlü bir yaklaşımdır. Eudoxos’un bu yaklaşımı, sayıların büyüklüklerine göre kıyaslanabileceğini ve bu sayede oranların tanımlanabileceğini gösterdi. Bu fikir, çok sonraları Richard Dedekind tarafından matematiksel olarak geliştirildi ve “Dedekind kesmesi” adını aldı.
Tüketme Yöntemi Nedir?
Eukleides’in Elementler adlı eserinin 10. kitabının başında, daha sonra “tüketme yöntemi” olarak adlandırılacak bir alan hesaplama tekniği anlatılır. Bu yöntemde iki farklı büyüklük alınır ve büyük olanın yarısından fazlası çıkarılır. Kalanın da yine yarısından fazlası alınarak işlem adım adım sürdürülür. Bu süreç devam ettikçe, sonunda geriye kalan miktar, küçük olan büyüklükten daha az olur.
Tüketme yöntemi, bir yüzeyin ölçüsünü istenilen hassaslıkta belirlemeye yarar. Örneğin bir dairenin alanı, içine yerleştirilen çokgenlerle bu şekilde hesaplanabilir. Bu yöntem, Arşimet Aksiyomu olarak bilinen temel bir ilkeye dayanır. Aksiyoma göre, iki büyüklükten birinin yeterince büyük bir katı alınırsa, bu kat diğerinden büyük olur.
Tüketme Yöntemi, İntegral kavramının Antik Çağ’daki karşılığıdır denebilir. Eudoxus bu yöntemi ustaca kullanarak birçok sonucu ispatlamıştır. Bu yaklaşım Eudoksos’un buluşudur. Arşimet de bunu açıkça belirtmiş ve aksiyomu Eudoksos’a atfetmiştir.
Elementler adlı eserin 12. kitabı, alanlar ve hacimlerle ilgilidir. Bu bölümde yer alan teoremlerin ve ispatların çoğu, Eukleides’in Eudoksos’tan aldığı çalışmalara dayanır. Kitaptaki 2. teorem, dairelerin alanlarının çaplarının kareleriyle orantılı olduğunu söyler. Benzer biçimde, 18. teoremde de kürelerin hacimlerinin çaplarının küpleriyle orantılı olduğu gösterilir.
2. ve 18. teoremler arasında yer alan bölümler, piramit ve konilerin hacimlerinin hesaplanmasıyla ilgilidir. Bu hacim formüllerini daha önce Demokritos (MÖ 460–370) bilse de, Arşimet’in Küre ve Silindir Üzerine adlı eserine göre, bu formüllerin ilk kesin ispatını yapan kişi Eudoksos’tur.
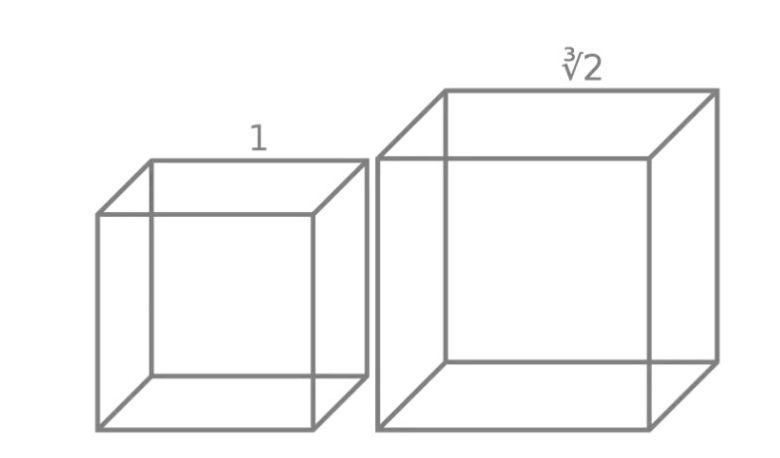
Eudoksos ayrıca ünlü Delos problemi yani bir küpün hacmini iki katına çıkarma sorusuyla da ilgilenmiştir. Eratosthenes’e göre, bu sorunun grafiksel bir çözümünü bulmuştur. Ancak bu yöntemin detayları günümüze ulaşmamıştır. Platon ise bu yaklaşımı eleştirmiştir;
Astronomi Bilimine Katkıları
Eudoxos, gözlemlerle matematiksel astronomi arasında sistematik bir bağ kuran ilk teorisyendi. Gök cisimlerinin hareketini açıklamak için geliştirdiği Eş Merkezli Küreler Teorisi, bilimsel astronominin temellerini attı. Bu teoriyle Antik Çağ’da bilinen 5 gezegenin (Merkür, Venüs, Mars, Jüpiter, Satürn) hareketlerini açıklamaya çalıştı.
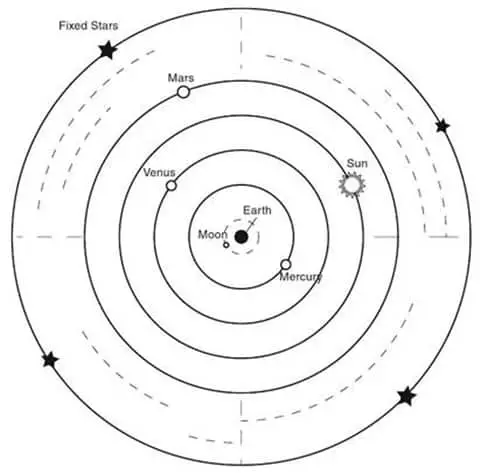
Eudoxos, tüm göksel hareketlerin dairesel ve düzenli olduğunu varsaydı. Her gezegenin, ortak merkezli ama farklı eksenlere sahip iç içe kürelerle temsil edildiğini savundu. Küreler birbirine bağlıydı ve hareketleri birleşerek gezegenin karmaşık yörüngesini oluşturuyordu. Dünya hareketsizdi ve merkezde yer alıyordu; onun etrafını sırasıyla Ay, gezegenler ve yıldızları taşıyan küreler sarıyordu.
Bu modelde, her gezegen dört küreyle temsil edilir: biri günlük hareket, biri yıllık döngü, kalan ikisi ise gezegenin duraklama ve gerileme hareketlerini açıklar. Eudoxos, bu kuramı fiziksel değil, geometrik bir model olarak sundu.
Güneş saatini ve bir yılın 365 gün 6 saat olduğunu ilk açıklayan bilim insanı da yine Eudoxos’tur. Geliştirdiği bu model, Kepler’e kadar yaklaşık 2000 yıl boyunca astronomiye yön verdi.

Ne yazık ki Eudoxus’un çalışmalarından hiçbiri günümüze kadar ulaşamamıştır. Başarılarının bir kısmı, Aristoteles, Arşimet ve Hipparchus’un çalışmalarındaki alıntılar ve referanslar sayesinde öğrenilmiştir. Böyle bir adamın adını Ay’daki bir kratere vermek yetmezdi elbette. Ancak Mars’taki bir krater de Eudoxus’un adını taşır.
Kaynaklar ve ileri okumalar:
- Eudoxus of Cnidus. (Erişim Tarihi: 23.05.2020) https://web.calstatela.edu/
- Murdin, P.. (2000). Eudoxus of Cnidus (c. 400-c. 347 BC). Encyclopedia of Astronomy and Astrophysics. 10.1888/0333750888/3609.
- Mendell, Henry Ross. “Eudoxus of Cnidus”. Encyclopedia Britannica, 29 Feb. 2024, https://www.britannica.com/biography/Eudoxus-of-Cnidus. Accessed 1 October 2024.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel