Basit görünse de, Euler’in Çokyüzlü Formülü, matematikçileri 4000 yıldan fazla bir süredir büyüleyen, “çokyüzlü” dediğimiz üç boyutlu katıların temel bir özelliğini özetler. Bu formül ünlü İsviçreli matematikçi Leonhard Euler’in (1707 – 1783) adını taşır.

On dokuzuncu yüzyılın sonlarına doğru matematikçiler alışılmış geometriden farklı bir anlayış geliştirdi. Başlangıçta bu alana “analysis situs”, yani konumun analizi denildi. Fakat kısa sürede yerleşen ad topoloji oldu.
Topolojinin kökeni, Descartes’ın 1639’da düzgün çokyüzlüler üzerine düşünürken fark ettiği ilginç bir sayısal düzene dayanır. Descartes düzgün çokyüzlülerle ilgilenirken dikkat çekici bir sayısal düzen fark etti. Küpte 6 yüz, 12 ayrıt ve 8 köşe vardır; 6 − 12 + 8 = 2 eder.
On iki yüzlüde 12 yüz, 30 ayrıt ve 20 köşe vardır; 12 − 30 + 20 = 2 olur. Yirmi yüzlüde 20 yüz, 30 ayrıt ve 12 köşe vardır. Yani 20 − 30 + 12 yine 2 verir. Aynı ilişki düzgün olsun olmasın, herhangi bir çokyüzlü için geçerlidir. Yüz sayısı F, ayrıt sayısı E ve köşe sayısı V ise F − E + V = 2 olur.
Descartes bu bağıntıyı küçük bir merak unsuru olarak gördü ve yayımlamadı. Oysa daha sonra matematikçiler bu basit eşitliği, yirminci yüzyıl matematiğinin büyük başarı alanlarından biri olan topolojinin ilk adımlarından biri olarak değerlendirdi.
Euler Çokyüzlü Formülü Nedir?
On dokuzuncu yüzyılda saf matematiğin üç temel dalı cebir, analiz ve geometriydi. Yirminci yüzyılın sonunda ise yerini cebir, analiz ve topoloji aldı. Topoloji, iki nesneyi ancak biri diğerine yırtmadan ya da kesmeden dönüştürülebiliyorsa aynı kabul eder. Bu dönüşümde yalnızca bükme, germe ve sıkıştırma işlemlerine izin verilir. Önemli olan tek şey sürekliliktir.
Elbette Descartes, bütün bu gelişmeler henüz çok uzaktaydı. Bu bağıntıyı kanıtlayıp yayımlayan kişi, tarihin en üretken matematikçisi olan Euler’dir.
Euler formülü önemli bir sonuç verir. Bir cismi basitleştirirken yüzleri birleştirebiliriz ya da ayrıt ve köşeleri kaldırabiliriz. Her kaldırılan yüzle birlikte bir ayrıt da kaldırılırsa veya her kaldırılan köşeyle birlikte bir ayrıt silinirse F − E + V değeri değişmez.
Ancak burada önemli bir ayrıntı vardır. Descartes’ın bağıntısı her cisim için geçerli değildir. Bunun en tanıdık karşı örneklerinden biri bir resim çerçevesidir. Dikdörtgen kesitli dört tahta parçanın köşelerde 45 derecelik kesimlerle birleştirildiğini düşünelim.
Her parça 4 yüz katkısı yapar, toplam F = 16 olur. Her parça 4 ayrıt getirir, köşe birleşimleri de ek ayrıtlar oluşturur ve E = 32 çıkar. Ayrıca her köşede 4 köşe noktası bulunur, V = 16 olur. Bu durumda F − E + V = 0 sonucu ortaya çıkar.
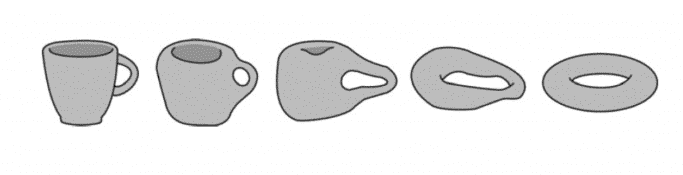
Demek ki resim çerçevesi ile küp arasında temel bir fark vardır ve F − E + V değişmezi bu farkı ortaya çıkarır. Bu fark da temelde topolojilerinden kaynaklanmaktadır. Aynı durum bir küre ve bir torus için de geçerlidir.
Torusa benzeyen, ancak iki ya da daha fazla deliği olan cisimler de vardır ve aynı değişmez bunlar hakkında da bilgi verir. İki delikli torusa dönüştürülebilen her cisim için F − E + V = −2 olur. Genel olarak g delikli bir torusa dönüştürülebilen her cisim F − E + V = 2 − 2g bağıntısını sağlar.
Euler Çokyüzlü Formülü Ne İşe Yarar?
Descartes ve Euler’in başlattığı düşünce çizgisi, böylece nicel bir özellik ile nitel bir özellik arasında bağ kurar. Yüz, ayrıt ve köşe sayıları gibi sayısal veriler, cismin delik taşıyıp taşımaması gibi yapısal bir özelliği yansıtır. F − E + V ifadesine cismin Euler karakteristiği denir. Bu değer, yüzlerin, ayrıtların ve köşelerin nasıl seçildiğine değil, cismin kendisine bağlıdır. Bu nedenle cismin içsel bir özelliğidir.
Bu düşünceyi geliştirenler arasında Johann Listing ve August Möbius vardı. Listing “topoloji” adını yerleştirdi, Möbius ise sürekli dönüşümlerin önemini açıkça vurguladı.
Listing’in önemli fikri, Euler bağıntısının genellemelerini aramaktı. F − E + V ifadesi kombinatoryal bir değişmezdir; bir cismin yüzlere, ayrıt ve köşelere bölünmesine dayanan sayısal bir özelliktir. Buna karşılık delik sayısı g topolojik bir değişmezdi. Cisim sürekli biçimde nasıl esnetilip bükülürse bükülsün değişmez. Topolojik değişmezler şeklin nitel yapısını yakalar, kombinatoryal olanlar ise bu yapıyı hesaplamaya yarar. İkisi birlikte, şekilleri hem kavramsal hem de sayısal olarak anlamamızı sağlar.
Sonuç Olarak
Aslında bu formül, “delik” kavramını tek tek tanımlama gibi zor bir sorunu tamamen devre dışı bırakır. “Delik sayısı”nı, tek tek saymadan, doğrudan bu bağıntı üzerinden tanımlamış oluruz. Kürenin Euler karakteristiği 2, torusun ise 0’dır. Bu nedenle küreyi torusa sürekli biçimde dönüştürmek mümkün değildir.
Kaynaklar ve ileri okumalar için:
- Euler’s polyhedron formula; yayınlanma tarihi: 25 Temmuz 2020; Kaynak site: Plus Math. Bağlantı: Euler’s polyhedron formula/
- Topology 101: The Hole Truth. Yayınlanma tarihi: 26 Ocak 2021. Kaynak site: Quanta magazine. Bağlantı: Topology 101: The Hole Truth
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel