Antik çağda geometrinin en önemli problemlerinden biri, yalnızca işaretsiz bir cetvel ve pergel kullanarak verilen bir açıyı üç eşit parçaya bölme meselesiydi. Bu problemi çözme çabaları sırasında birçok dahiyane eğri ortaya çıktı. Bu eğrilerden biri de Elisli Hippias tarafından ortaya konmuştur.
Modern Olimpiyatlar denildiğinde sporcuların üstün performansı ve kıyasıya rekabeti akla gelir. Buna giderek daha gösterişli hâle gelen açılış ve kapanış törenleri eşlik eder. Oyunlar, kökenini MÖ 776’ya dayandırır ve antik dönemde MS 393’e kadar dört yılda bir düzenlenir. Yunanlar yarışmaları, Mora Yarımadası’nın batısındaki Elis bölgesinde gerçekleştirirdi. Hippias da bu coğrafyanın yetiştirdiği önemli isimlerden biridir.
Hippias hakkında güvenilir bilgilerin büyük bölümünü Platon’un üç diyaloğu sağlar. Bu metinlere göre Hippias yaklaşık MÖ 460’ta doğmuş, MÖ 400 dolaylarında ölmüş ve Platon’la çağdaş olmuştur. Ancak bu çağdaşlık iki taraf için de pek huzurlu geçmez.

Platon, Hippias’ı kendini beğenmiş, kibirli ve zihinsel açıdan sınırlı biri olarak tanımlamaktadır. Buna karşılık kaynaklar, Hippias’ın varlıklı, çok gezmiş ve olağanüstü bir hafızaya sahip olduğunu gösterir. Ayrıca matematik de dâhil olmak üzere kuramsal ve pratik pek çok alanda dersler verdiğini biliyoruz.
Hippias, Olimpiyat Oyunları’yla da güçlü bir bağ kurmuştur. Oyunlara düzenli biçimde katılmış, kazananların ilk listesini derlemiş ve müsabakalar sırasında yaptığı halka açık konuşmalarla ün kazanmıştır. Bu yazı bağlamında onu özel kılan ise, başlangıçta rastgele bir açıyı üçe bölmek amacıyla tasarladığı ve sonradan “kuadratriks” adını alan eğriyi icat etmesidir.
Hippias’ın başarısı, mevcut araçlarla yetinmeyip geometrinin sınırlarını genişletmesinden kaynaklanır. Bu genişleme, yeni bir geometrik eğri tanımlamasıyla somutlaşır. Kuadratriks, antik geometrinin doğru ve çember dışında tanımladığı ilk özel eğridir ve iki hareketin eşzamanlı ilerlemesiyle ortaya çıkar.
Matematikçiler, elips, parabol ve hiperbol gibi konik kesitleri sistemli biçimde incelemeye başlamadan yaklaşık 60–70 yıl önce bu eğriyi geliştirmiştir.
Kuadratriks Eğrisi İle Açıyı Üçe Bölme
ABCD birim kare olsun. Başlangıçta üst kenar CD yerindedir. Aynı anda iki hareket başlar. CD kenarı, sabit bir hızla yukarıdan aşağıya doğru kayar ve sonunda alt kenar AB’ye ulaşır. Aynı anda, A noktasından çıkan bir doğru, A etrafında sabit hızla dönmeye başlar ve sonunda AB doğrusu ile çakışır.
Hareket boyunca, aşağı inen CD kenarı ile A’dan dönen doğrunun kesiştiği noktayı F olarak işaretleyelim. F noktası zamanla yer değiştirir. F’nin izlediği yol, şekilde kırmızıyla gösterilen kuadratrikstir.
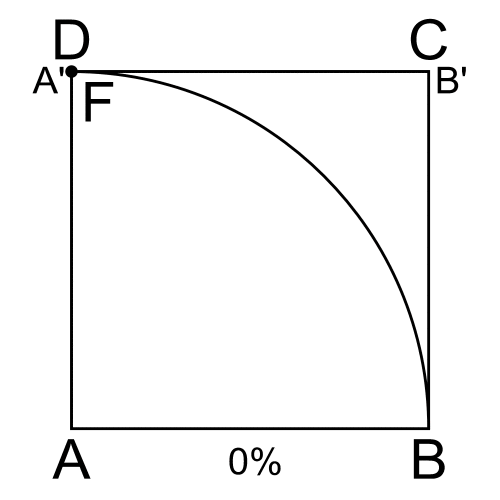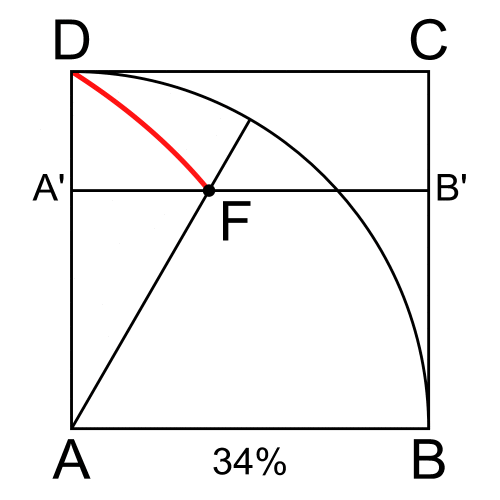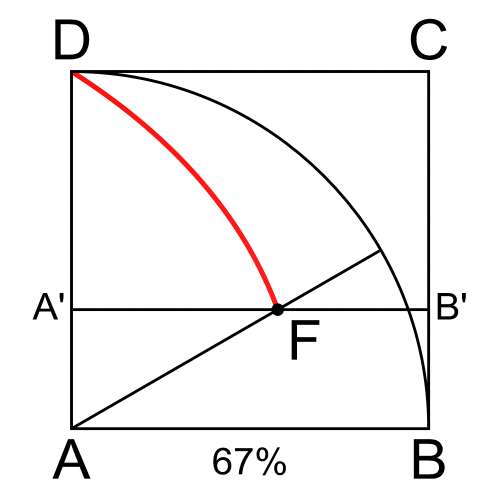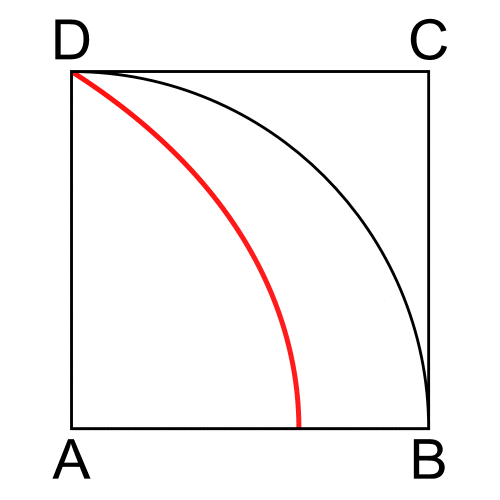
Bu yapım yöntemi ciddi eleştiriler almıştır. Çünkü kuadratriksin kurulması için gerekli eşzamanlı hareket sorunludur. Bu hareket, karenin bir kenarının çeyrek çemberin çevresine oranının tam olarak bilinmesini gerektirir. Böyle bir oranı bilmek, yarıçapı verilen bir çemberin çevresini, dolayısıyla π’yi tam olarak bilmek anlamına gelir.
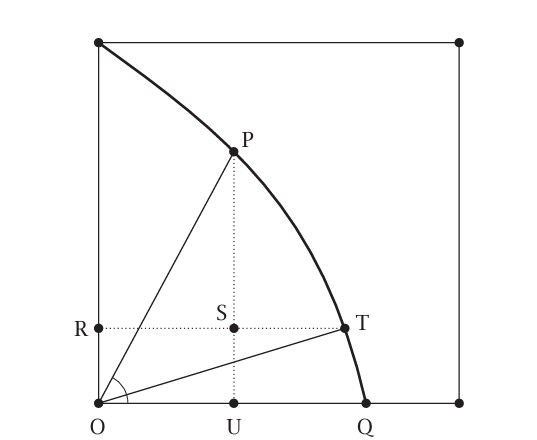
Şekilde ∠POQ açısını ele alalım. P noktasından OQ doğrultusuna bir dik indirir ve PU doğru parçasını elde ederiz. Bu doğru parçasını S noktasında üç eşit parçaya böleriz. S’den geçen yatay doğruyu çizip R ve T noktalarını belirleriz. Son olarak O ile T’yi birleştiririz. Elde edilen ∠TOQ açısı, başlangıçtaki ∠POQ açısının tam olarak üçte birine eşittir.
Sonuç Olarak
Kuadratriks, tartışmalı olsa da ortaya çıkış amacını yerine getirir. Bazı açılar gerçekten üçe bölünebilir; 90°, 72° ve 27° bunun örnekleridir. Asıl mesele, cetvel ve pergel kullanılarak her açıyı üçe bölen genel bir yöntemin var olup olmadığını belirlemektir. Böyle bir yöntemin bulunmadığı ancak çok daha sonra kanıtlanacakt
Kaynaklar ve ileri okumalar:
- Kopp, Ekkehard. (2020). Chapter 9.: Counting beyond the finite. 10.11647/obp.0236.09.
- Heilbron, J.L.. “Trisecting the Angle: The Quadratrix of Hippias”. Encyclopedia Britannica, 27 Apr. 2001, https://www.britannica.com/topic/Trisecting-the-Angle-The-Quadratrix-of-Hippias-1688521. Accessed 22 May 2024.
- Quadratrix of Hippias; https://en.wikipedia.org/wiki/Quadratrix_of_Hippias
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






Yazabiliriz dediğiniz eşitlik nerede , bunu bir deklemle ifade edersek dediğiniz denklem nerede ?
Bu arada ; denklem= eşitlik
Mükemmele yakın bir şekilde açıyı üçe bölme yöntemini biliyorum. Mükemmel mi değil mi bi bakmak isteye bilirsiniz belki 🙂