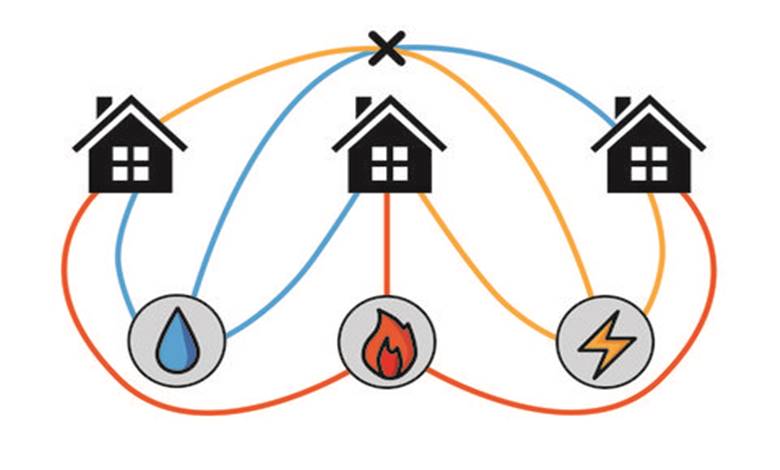
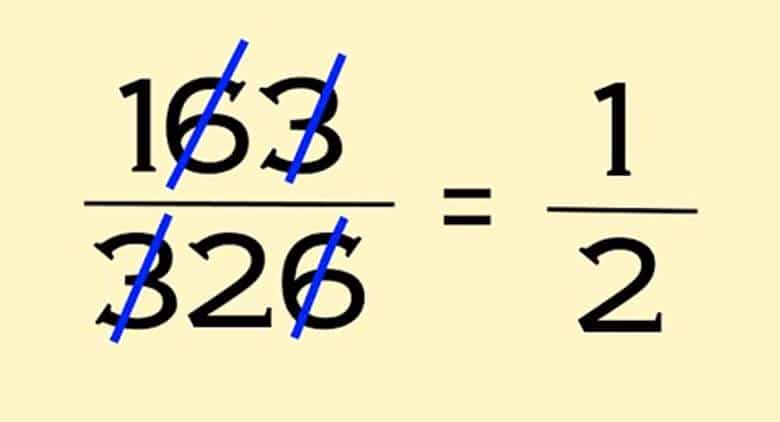Dünyanın birçok yerinde matematikçiler yıllardır üç kulübe problemi, elektrik-su-doğal gaz problemi ya da üç ev üç kuyu problemi adıyla bilinen…
Beyin Jimnastiği
Verilen bir kesri sadeleştirmek basit bir işlem gibi görünür. Ancak özellikle ilköğretim düzeyindeki öğrencilerin sık yaptığı bir hata vardır. Bu…
Go oyunu, büyülü bir oyundur. Kurallarını öğrenmesi 10 dakika sürer. Oyunu öğrenmesi ise ömür tüketir.
Tarihin karanlık dönemlerinden günümüze yalnızca adıyla ulaşabilmiş figürler vardır. Diophantus da bu isimlerden biridir. Onun kim olduğu, neye benzediği ya…
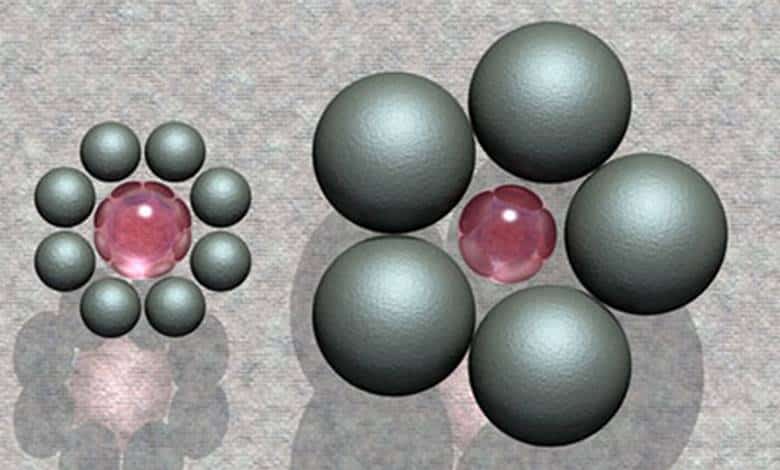
Görsel yanılsamalar, çevremizi hızlı ve verimli algılamamıza yardımcı olan görsel sistemin zaman zaman yanılmasından kaynaklanır. Bu tür hatalar, beynimizin karmaşık…
David Hilbert’in “sonsuz otel paradoksu” (Hilbert’s Hotel), sonsuzluk kavramının sezgilere aykırı doğasını gözler önüne seren çarpıcı bir düşünce deneyidir. David…
Dünyanın çevresine bir ip dolasak ne olurdu? İlk bakışta çocukça ya da anlamsız gibi görünen bu soru, aslında sezgilerimize meydan…
Ay’ı (veya Güneş’i) ufka yakın gördüyseniz, bu yanılsamayı deneyimlemişsinizdir. Ay, ufukta devasa görünür ve tepede olduğu zamankinden çok daha büyük…
Bazen matematik öylesine zarif ve etkileyici bir şekilde karşımıza çıkar ki, insan bunu kendi keşfetmemiş olsa bile “Eureka!” diye haykırmak…
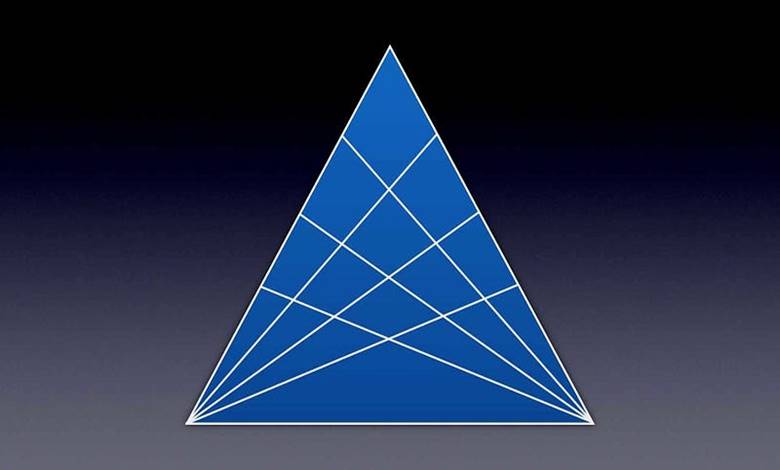
İnternette vakit geçiren birçok kişi, matematiğe ilgi duysun ya da duymasın, zaman zaman kendini bir mantık veya görsel algı sorusunu…
Matematikte sorulara genellikle net cevaplar verilir. Ancak 2000 yılında popüler hale gelen ve o günden bu yana matematikçileri ve filozofları…
Bu yazıya konu olan soru, SAT (Scholastic Aptitude Test) sınavında bugüne kadar sorulmuş en zor matematik sorularından biri olarak kabul…