Dünyanın en zor ve en ünlü matematik problemini kesin olarak belirlemek mümkün olmasa da, 1859 yılında Bernhard Riemann tarafından ortaya atılan ve o zamandan beri matematikçileri derinden etkileyen Riemann Hipotezi, bu unvana güçlü bir aday olarak öne çıkıyor.
Riemann Hipotezi, David Hilbert’in 1900 yılında yayımladığı çözülmemiş 23 problem listesindeki sekizinci problemdir. Ayrıca, 2000 yılında Clay Mathematics Institute tarafından belirlenen “Millennium Prize Problems” arasında da yer almakta ve en önemli ikinci problem olarak kabul edilmektedir.
Bu hipotezi çözen kişi, adını matematik tarihine altın harflerle yazdıracaktır. Üstelik, bu problem “Milyon Dolarlık Problemler” arasında yer aldığından, çözümü yalnızca bilimsel değil, maddi bir ödül de getirecektir.
Riemann Hipotezi, özünde asal sayıların sayı doğrusu üzerindeki dağılımıyla ilgilidir. Hipotezin cevabı basit bir “evet” ya da “hayır” olabilir; ancak bu sonuca ulaşmak, oldukça karmaşık ve zorlu varsayımları ispatlamayı gerektirir. Eğer hipotez ispatlanırsa, bu durum matematik dünyasında uzun yıllardır elde edilen en büyük başarılardan biri olarak kabul edilecektir.
Günümüzde birçok teorem Riemann varsayımına dayanır. Bu varsayımın kanıtı, aynı anda pek çok başka teoremi de doğrular. Bu durum, inatçı ve zorlayıcı bu problemle uğraşmak için güçlü bir motivasyon oluşturur.
Her Şey Nasıl başladı?
Riemann Hipotezi’nin ne olduğunu anlamak için öncelikle asal sayıların ne olduğuna bakmamız gerekir. Matematikçiler için asal sayılar, sayılar evreninin atomları gibidir; yani, tüm doğal sayıların temel yapı taşlarıdır.
Ancak sorun şudur. Asal sayılar basit bir düzen izlemez. Doğal sayılar arasında rastgele dağılmış gibidirler. Yani, bir asal sayıyı tespit ettikten sonra bir sonraki asal sayının nerede yer alacağını tahmin etmek oldukça güçtür. Bu nedenle, matematikçiler asal sayıların sayı doğrusu üzerindeki dağılımını incelerler.

Asal sayılara ilgi binlerce yıl öncesine uzanır. Öklid, MÖ 300 dolaylarında asal sayıların sonsuz olduğunu kanıtladı. Bu ilgi hiç kaybolmadı. Ancak bu temel yapı taşları hakkında yeni ve önemli sonuçlar ancak 18. yüzyılda elde edildi.
Carl Friedrich Gauss, 15 yaşındayken asal sayıların sayı doğrusu boyunca seyrekleştiğini fark etti. Daha sonra asal sayı teoremi diye anılan bu gözlem, ancak yüz yıl sonra kanıtlandı. Teorem, 0 ile n arasındaki aralıkta yaklaşık olarak n/ln(n) tane asal sayı bulunduğunu söyler. Başka bir ifadeyle, asal sayı teoremi matematikçilere, asal sayıların sayı doğrusu üzerindeki tipik dağılımını tahmin etme olanağı sunar.
Ancak asal sayıların gerçek sayısı, teoremin verdiği tahminden bazen sapar.. Örneğin asal sayı teoremine göre 1 ile 100 arasında yaklaşık 100/ln(100) ≈ 22 asal sayı vardır. Oysa gerçekte bu sayı 25’tir. İşte Riemann hipotezi burada devreye girer. Bu hipotez, matematikçilere bu sapmayı tahmin etmenin bir yolunu sunar.
Riemann Hipotezi Nedir?
Riemann hipotezi, asal sayıların tek tek nerede bulunduğunu söylemez. Bunun yerine, sayı doğrusu üzerindeki dağılımlarının belirli bir düzen izlediğini ileri sürer.
Hipoteze göre asal sayıların yoğunluğu, asal sayı teoreminde anlatıldığı gibi giderek azalır. Buna karşın, bu azalan yoğunluğa uygun biçimde dengeli biçimde yayılırlar. Yani asal sayıların tamamen yok olduğu geniş aralıklar oluşmaz. Aynı şekilde, belirli bölgelerde aşırı birikmeler de görülmez.
Bu durumu bir odadaki havanın molekülleriyle düşünebilirsiniz. Zemine yakın bölgelerde yoğunluk biraz daha fazladır. Tavana doğru yoğunluk azalır. Ancak moleküller bu değişime rağmen odaya düzenli biçimde dağılır. Odada hiçbir yerde gerçek bir boşluk oluşmaz.

1859’da Alman matematikçi Bernhard Riemann (1826–1866) Berlin Akademisi’ne “Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse” başlıklı bir makale sundu. Aslında bu makale onun sayı teorisi üzerine yayınladığı tek makale idi.
Riemann Zeta Fonksiyonu Nedir?
Riemann, zeta fonksiyonu ζ(s) adı verilen özel bir fonksiyon üzerinde çalıştı. Bu fonksiyon, doğal sayıların s kuvvetine yükseltilmiş terslerinin sonsuz bir toplamıdır.
Riemann’dan önce de matematikçiler, bu tür zeta fonksiyonlarının asal sayılarla bağlantılı olduğunu biliyordu. Riemann’ın asıl yeniliği, s değişkenini gerçek sayılarla sınırlamamasıydı. Karmaşık sayıları da işin içine katmasıydı.
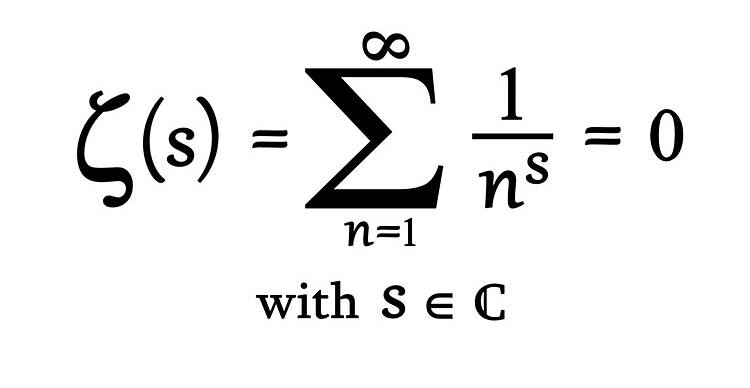
Riemann’ın ele aldığı karmaşık zeta fonksiyonunu, bir düzlemin üzerine çizilmiş üç boyutlu bir yüzey gibi hayal edebiliriz. Yüzeyin bazı yerleri yükselir, bazı yerleri alçalır. Bu yüzey üzerinde özellikle önemli noktalar vardır. Bu noktalar, zeta fonksiyonunun değerinin sıfır olduğu yerlerdir.
Riemann kısa sürede önemli bir sonuç elde etti. Zeta fonksiyonunun, gerçek kısmı 1’den büyük olan değerlerde hiçbir sıfırı yoktur. Başka bir deyişle, x = 1 doğrusunun sağında kalan bölgede bu matematiksel manzara hiçbir zaman deniz seviyesine inmez.
Gerçek kısmın negatif olduğu durumlarda ise zeta fonksiyonunun sıfırları hesaplanabilir. Bunlar, gerçek eksen üzerinde x = –2, –4, –6 gibi noktalarda yer alır. Ancak Riemann’ı asıl ilgilendiren bölge başkaydı. Bu bölge, gerçek kısmı 0 ile 1 arasında kalan, “kritik şerit” olarak adlandırılan aralıktı.
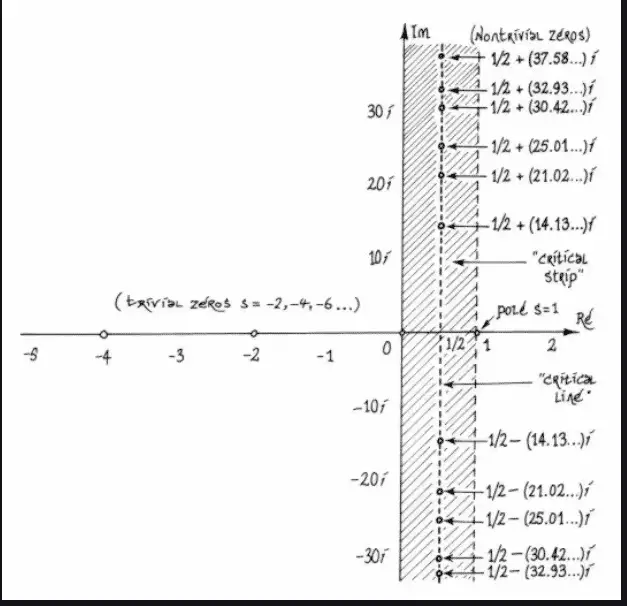
Riemann, kritik şerit içinde zeta fonksiyonunun sonsuz sayıda sıfırı olduğunu biliyordu. İlginç olan şuydu: Bu sıfırların tamamı, x = 1/2 doğrusu üzerinde görünüyordu. Bunun üzerine Riemann şu varsayımı ortaya attı: Kritik şerit içindeki tüm zeta fonksiyonu sıfırlarının gerçek kısmı x = 1/2’dir.
Bu iddia, eğer doğruysa, asal sayı teoreminin verdiği tablo güvenilirdir; beklenmedik büyük sapmalar ortaya çıkmaz.
Riemann Hipotezi Neden Önemlidir?
Bugüne kadar zeta fonksiyonunun milyarlarca, hatta trilyonlarca sıfırı incelenmiştir. Sayıları 1013’ü aşan bu sıfırların tamamı, karmaşık düzlemdeki kritik şerit içinde yer alan x=21 doğrusu üzerinde bulunur. Ancak bu durum, tek başına Riemann Hipotezi’nin bir kanıtı sayılmaz. Varsayımı çürütmek için, bu düzenin dışında yer alan tek bir sıfır bulmak yeterlidir. Bu nedenle amaç, kritik şerit içinde x=21 doğrusu dışında hiçbir sıfır bulunmadığını kesin olarak göstermektir.
Riemann Hipotezi, asal sayılarla doğrudan ilgili olmasına rağmen, görünüşte alakasız pek çok alanda da karşımıza çıkar. Bu nedenle, hipotezin kanıtlanması (ya da çürütülmesi) yalnızca sayı teorisini değil, matematiğin tamamını ve hatta fizik gibi diğer bilim alanlarını da derinden etkiler.
Riemann Hipotezi’nin atom altı evrenle incelikli fakat doğrudan bir bağlantısı olduğu düşünülmektedir. Nükleer fizikte, zeta fonksiyonunun sıfırlarının dağılımı ile ağır bir element olan uranyum atomunun enerji seviyelerinin dağılımı dikkat çekici biçimde örtüşmektedir. Bu benzerlik, kuantum mekaniği ile asal sayılar arasında bir bağ olabileceğini düşündürmektedir — ki bu bile başlı başına son derece çarpıcı bir fikirdir.
Sonuç olarak
Riemann’ın hipotezini dünyaya duyurmasının üzerinden 150 yıldan fazla zaman geçti. Bu süre zarfında, bir kanıtın yokluğu, matematiğin kalbinde açık bir boşluk hâline geldi. Sayısı kesin olarak bilinmese de, muhtemelen yüzlerce araştırmacı bu hipotezi kanıtlamak için çaba harcadı. Ancak bugüne kadar hiçbir çalışma, geçerli bir ispat olarak kabul edilmedi.
1900 yılında, matematikçilerin çözmesi için 23 temel problem belirleyen David Hilbert, sekizinci soruyla (Riemann Hipotezi) ilgili şöyle demişti. “Eğer 500 yıl uyuyup uyanacak olsam, uyanır uyanmaz ilk sorum şu olurdu: Riemann Hipotezi ispatlandı mı?”
Umarız cevabını öğrenmek için o kadar uzun süre beklemek zorunda kalmayız…
Kaynaklar ve ileri okumalar için:
- A whirlpool of numbers; yayınlanma tarihi: 1 Mayıs 2003; Bağlantı: https://plus.maths.org
- Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved? Yayınlanma tarihi: 27 Ekim 2018. Kaynak site: Conversation. The Conversation. Bağlantı: Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved?
Matematiksel





