Dünyayı algılayış biçimimiz ve buna bağlı olarak verdiğimiz kararlar, çoğu zaman 250 yıldan daha uzun bir süre önce, sessiz sedasız çalışan İngiliz bir matematikçi ve ilahiyatçı tarafından geliştirilen basit bir teoreme dayanır. Thomas Bayes’in gizlice üzerinde çalıştığı bu fikirler, ancak ölümünden sonra yayımlanabilmiştir.
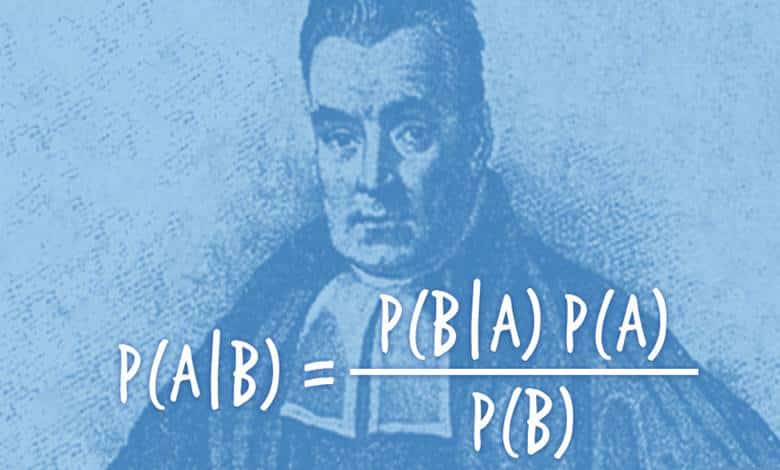
Bayes Teoremi, II. Dünya Savaşı sırasında Enigma şifrelerinin kırılmasında kilit bir rol oynamış; günümüzde ise bilimden teknolojiye, tıptan yapay zekâya kadar pek çok alanda belirsizlikle başa çıkmanın temel araçlarından biri hâline gelmiştir. Peki bu teorem tam olarak nasıl çalışır?
Bayes Teoremi İle Nasıl Tanıştık?
1702–1761 yılları arasında yaşamış Presbiteryen bir din adamı olan Rahip Thomas Bayes, anlaşılan tam anlamıyla bir matematik meraklısıydı. İngiltere Kilisesi’nden ayrılıkçı olduğu için Oxford ya da Cambridge’de eğitim alamamış, bunun yerine İskoçya Üniversitesi’nde öğrenim görmüştü. Büyük olasılıkla matematik bilgisinin önemli bir bölümünü de burada edinmişti.
İngiltere’ye döndükten sonra da matematikle uğraşmayı sürdürmüş, tartışma grupları düzenlemişti. Ölümünden sonra yayımlanan bir makalesinde Bayes, matematik ile teolojiyi karşı karşıya getiren bir probleme eğildi.

Makalesi, yaklaşık 250 yıl sonra hâlâ tartışılıyor. Ancak bunun nedeni teolojik yönü değil, bir etkiden yola çıkarak bir nedenin olasılığının hesaplanabileceğini göstermesidir.
Bir neden biliniyorsa, bu nedenin yol açacağı etkinin olasılığını tahmin etmek görece kolaydır. Buna ileri olasılık denir. Asıl zor olan ise ters yönde ilerlemektir. Bayes’in yaşadığı dönemde “ters olasılık” olarak adlandırılan bu problem, yani gözlenen bir etkiden hareketle altta yatan nedenin olasılığını çıkarsamak, çok daha karmaşıktır.
Ancak Bayes bunun neden zor olduğunu açıklamaya çalışmadı. Aksine bunu apaçık kabul ederek, yapılabilir olduğunu kanıtladı ve nasıl yapılacağını gösterdi.
Bayes Teoremi Nedir?
Bayes yönteminin nasıl çalıştığını görmek için, bir çayevindeki müşteriler üzerinden ilerleyelim. Diyelim ki gelen müşterilerin üçte ikisi çay içiyor. Çay içenlerin yarısı da simit alıyor. Bu durumda, müşterilerin ne kadarı hem çay hem simit sipariş eder?
Burada karmaşık bir hesap yoktur. Üçte ikinin yarısı üçte bir eder; yani müşterilerin üçte biri hem çay hem simit sipariş etmektedir.
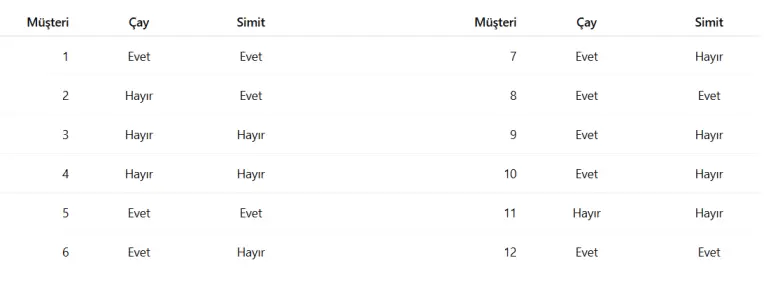
Kapıdan giren sonraki on iki müşterinin siparişlerini kaydettiğimizi varsayalım. Tablonun da gösterdiği gibi, müşterilerin üçte ikisi (1, 5, 6, 7, 8, 9, 10 ve 12 numaralı kişiler) çay sipariş etmiştir. Bu kişilerin yarısı da (1, 5, 8 ve 12 numaralı kişiler) simit almıştır. Dolayısıyla hem çay hem simit sipariş eden müşterilerin oranı gerçekten de (1/2) × (2/3) = 1/3’tür.
Bunu kural hâline getirmek için, bir müşterinin çay sipariş etme olasılığını , simit sipariş etme olasılığını ise ile gösterelim. Bir müşterinin zaten çay sipariş ettiğini biliyorsak, bu müşterinin simit sipariş etme olasılığını ifade eder. Benzer biçimde, müşterinin simit sipariş ettiği bilindiğinde çay sipariş etme olasılığıdır.
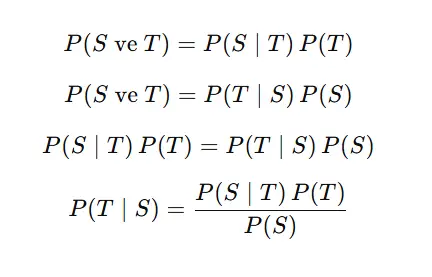
Bu denklem, Bayes kuralı olarak bilinir. Dikkatle bakıldığında, ters olasılık probleminin genel bir çözümünü sunduğu görülür. Bayes kuralının istatistikteki en önemli rolü de budur.
değerini doğrudan hesaplamadığımızı ve sipariş verilerini içeren tabloya erişimimiz olmadığını varsayalım. Buna rağmen bazı temel oranları hatırlayalım. Çay sipariş eden müşterilerin yarısı simit de almaktadır; müşterilerin üçte ikisi çay sipariş etmektedir ve 12 müşteriden beşi simit almaktadır.
Bu bilgilerle şu soruya yanıt verebiliriz: Simit alan müşterilerin ne kadarı çay da sipariş etmektedir? Kurala göre aşağıdaki eşitliği sağlayan değer 4/5 olmalıdır. Yani simit alan müşterilerin beşte dördü aynı zamanda çay da sipariş etmektedir.
Bayes Teoremi Günlük Hayatımızda Her Yerdedir
Bayes kuralı, belirli bir hipoteze olan inancımızı güncellemenin bir yolu olarak da görülebilir. Bu bakış açısı son derece önemlidir, çünkü geleceğe dair pek çok beklentimiz, geçmişte benzer olayların ne sıklıkla gerçekleştiğine dayanır. Bir restorana giren bir müşterinin büyük olasılıkla çay isteyeceğini düşünmemiz, daha önce karşılaştığımız benzer müşterilere dair deneyimlerimizin bir sonucudur.
Ancak müşteri önce simit sipariş ederse, bu beklenti daha da güçlenir. Hatta bu noktada “Yanında çay da ister misiniz?” diye sormak oldukça makul görünür. Bayes kuralı, bu gündelik akıl yürütme sürecine sayısal bir karşılık kazandırır.
Yukardaki tabloya göre, bir müşteri kapıdan içeri girdiği anda, yani henüz hiçbir sipariş vermemişken çay isteme olasılığı üçte ikidir. Bu, önsel olasılıktır. Müşteri simit sipariş ettiğinde ise elimizde daha önce sahip olmadığımız yeni bir bilgi ortaya çıkar. Bu yeni bilgiyle birlikte, müşterinin çay isteme olasılığı güncellenir ve olur. Başka bir deyişle, simit siparişi, çay isteyeceğine dair inancımızı daha güçlü hâle getirir.
Sonuç Olarak
Gördüğümüz gibi Bayes kuralı, biçimsel olarak koşullu olasılık tanımının oldukça basit bir sonucudur. Ancak epistemolojik açıdan bakıldığında durum hiç de basit değildir. Bayes kuralı, gerçekte kanıtla karşılaşıldığında inançların nasıl güncellenmesi gerektiğini söyleyen normatif bir ilke gibi çalışır.
Bayes kuralı, başka şeylerin yanı sıra şu iddiayı da içerir. Bir kişi T bilgisini öğrendikten sonra S’ye atfettiği inanç derecesi, T’yi öğrenmeden önce S ve T’ye birlikte atfettiği inanç derecesinden hiçbir zaman daha düşük olamaz. Ayrıca şu sonucu da ima eder. Bir kanıt ne kadar şaşırtıcıysa, yani ne kadar küçükse, bu kanıtın nedeni olduğu varsayılan S’ye duyulan inanç o kadar güçlü biçimde artmalıdır.
Bayesçi çıkarımda önsel olasılıkların hatalı kullanılması ciddi sonuçlar doğurur. Hukukta bu durum, “savcının yanılgısı” olarak bilinen adalet hatalarına yol açmaktadır.
Birleşik Krallık’ta yaşanan Sally Clark davası buna çarpıcı bir örnektir. Clark, 1999 yılında iki çocuğunu öldürdüğü iddiasıyla haksız yere mahkûm edilmiştir. Savcılık, iki bebeğin doğal nedenlerle ölme olasılığının son derece düşük olduğunu ileri sürmüş ve bu kadar düşük bir olasılığın annenin masum olamayacağını gösterdiğini savunmuştur.
Ancak bu argüman kritik bir noktayı göz ardı ediyordu. Bir annenin iki çocuğunu birden öldürme olasılığı da son derece düşüktü. Önsel olasılıkların bu şekilde tek taraflı ele alınması, Bayesçi akıl yürütmenin yanlış uygulanmasına ve sonuçta ciddi bir adalet yanılgısına yol açmıştır.
Kaynaklar ve ileri okumalar
- Maths in a minute: Bayes’ theorem; yayınlanma tarihi: 25 Ocak 201. Kaynak site: Plus math.; Bağlantı: Maths in a minute: Bayes’ theorem/
- Bayes’ Theorem: the maths tool we probably use every day, but what is it?. Yayınlanma tarihi: 23 Nisan 2017. Bağlantı: https://doi.org/10.64628/AA.snk3kj7p7
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel