Bambu ağaçlarının çiçeklenme döngüleri, sadece biyolojik değil, aynı zamanda matematiksel bir düzene de sahip gibi görünüyor. Yapılan araştırmalar, bu döngülerin çoğunlukla küçük asal sayıların çarpımıyla oluştuğunu ortaya koyuyor.

1960’ların sonlarına doğru, Çin anakarasına özgü Phyllostachys bambusoides adlı bambu türü çiçek açtı. Bu tür zamanla Japonya’ya, oradan da Amerika Birleşik Devletleri ve diğer ülkelere yayılmıştı. En dikkat çekici olan ise çiçeklenmenin yalnızca tek bir coğrafyada değil, dünya genelinde farklı kıtalardaki bambular arasında neredeyse eş zamanlı gerçekleşmesiydi. Aralarındaki binlerce kilometrelik mesafeye rağmen, bu bambular aynı anda çiçek verdi.
Bitkiler rüzgârla taşınan polenler üretti; döllenen bireyler tohum oluşturdu ve bu tohumlar toprağa düştü. Ardından, boyları 22 metreye kadar ulaşabilen bu dev bambuların tamamı yaşam döngülerini tamamlayarak öldü. Yerlerine ise tohumlardan filizlenen yeni bireyler geçti. Bugün hayatta olan bu nesil yaklaşık 50 yaşında ve henüz çiçeklenmedi. Bir sonraki büyük çiçeklenme dalgası ise ise yaklaşık 2090 yılında gerçekleşecek.
Bambu Ağaçları Belirli Bir Düzenle Çiçek Açar
Bu bilgilerin ayrıntılı şekilde bilinmesinin nedeni, Çinli bilim insanlarının yüzyıllar boyunca yürüttüğü titiz gözlemlerdir. Örneğin, Çin anakarasındaki Phyllostachys bambusoides türünün 999 yılında çiçek açtığı belgelenmiştir. O dönem bu olaya tanıklık edenler, daha önce benzer bir durumla karşılaşmamıştı. Bambu ormanları topluca çiçeklenmiş, ve yeni nesil bambular 1114 yılına kadar tekrar çiçeklenmemiştir.
Bu tür Japonya’ya ulaştıktan sonra orada da benzer gözlem ve kayıt alışkanlıkları sürdürülmüştür. Japon kaynaklarında, 1700’lü yılların başında ve 1844-1847 yılları arasında meydana gelen toplu çiçeklenmeler detaylı şekilde belgelenmiştir. 1960’ların sonundaki küresel çiçeklenme dalgası ise bu yaklaşık 120 yıllık döngünün doğal bir devamıydı.
Bu şaşırtıcı biyolojik takvim tek başına oldukça etkileyici olsa da, benzer şekilde başka bambu türlerinde de uzun süreli çiçeklenme döngülerinin görüldüğü bilinmektedir. Örneğin, Bambusa bambos adlı tür her 32 yılda bir çiçek açarken, Phyllostachys nigra f. henonis ise yaklaşık 60 yılda bir çiçeklenme gösterir.
Bambular Matematik Biliyor mu?
Bu dikkat çekici döngüler, Harvard Üniversitesi’nden biyologlar Carl Veller, Martin Nowak ve Charles Davis’in ilgisini çekti. Üçlü, bambuların uzun çiçeklenme aralıklarının arkasında basit aritmetik prensiplerin olabileceğini öne sürdü.
Ekolog Daniel Janzen’in 1970’lerde bambuların aynı anda çiçek açarak avcı hayvanlara karşı bir strateji geliştirdiğini öne sürmüştü. Bu toplu çiçeklenmelerde çor fazla tohum olduğu için, hayvanlar hepsini yiyemiyordu. Böylece hayatta kalan tohumlar yeni nesli oluşturuyordu.
Ayrıca bu senkronizasyon, zamanla genetik olarak da yerleşmişti. Erken çiçeklenen bireyler daha az tohum ürettiği için genlerini aktarma şansı düşüyordu. Bu da döngünün dışına çıkanların doğal olarak elenmesine yol açıyordu. Ancak araştırmacılar yanıtsız kalan bir soruya dikkat çekti. Bu karmaşık sistem ilk kez nasıl ortaya çıktı?
Bu soruya bir cevap için, bilim insanları, bambuların biyolojik özelliklerini temel alarak bir matematiksel model geliştirdi. Bu modelin başlangıç noktası, neredeyse tüm bireylerin her yıl çiçek açtığı varsayımsal bir bambu ormanıydı.
Bambular Aynı Anda Çiçek Açacaklarını Nasıl Biliyor?
Ancak bu popülasyonda bazı bireylerde mutasyon mevcuttu. Bu mutant bambular, yılda bir yerine iki yılda bir çiçek açıyordu. Üstelik bu iki yıllık döngüye sahip bireylerin bazıları yalnızca çift yıllarda, bazıları ise tek yıllarda çiçek açıyordu.

Zamanla, bu iki yılda bir çiçeklenen bireyler çoğalmaya başladı. Bu durum, her yıl çiçek açarak tohum üreten bireylerin sayısını giderek azalttı ve zaman içinde de yok oldular. Eğer bu yok oluş belirli bir yıla denk gelirse—örneğin bir tek yıla—o yıl çiçeklenen iki yıllık bireyler de zarar görür. Aynı durum çift yıllar için de geçerlidir. Sonuç olarak, geriye sadece belirli bir yıla bağlı olmayan iki yıllık bireyler kalır ve zamanla tüm ormanda çiçeklenme döngüsü iki yıla sabitlenir.
Ormanda yalnızca iki yılda bir çiçeklenen mutantların değil, üç yıl ya da daha uzun aralıklarla çiçek açan bireylerin de bulunması mümkündür. Hangi döngünün galip geleceği ise büyük ölçüde şansa bağlıdır. Çünkü bambuların bir yılda ne kadar tohum vereceği, hava durumu gibi öngörülemeyen koşullara göre değişir.
Ancak hangi döngü öne çıkarsa çıksın, ormandaki tüm bireyler zamanla bu yeni takvime uyum sağlar. Janzen’in de öne sürdüğü gibi, senkronizasyonun dışına çıkan bireyler ise elenir ve yok olur.
Ancak bu düzenin istisnai bir yönü de var. Bir mutant bambu, orijinal çiçeklenme döngüsünün katı olan yeni bir döngü geliştirebilir. Örneğin, iki yılda bir çiçek açan bir bambu, zamanla dört yılda bir çiçek açmaya başlar.
Bu durumda, dört yılda bir çiçeklenen bireyler, her çiçeklenme döneminde hâlâ iki yıllık bambularla aynı anda çiçek açtıkları için korunmaya devam eder. Üstelik daha uzun bekleme süresi onlara avantaj sağlar. Bu süre boyunca daha fazla tohum üretme potansiyeline sahiptirler.
Üstelik belirli koşullar altında bu durum popülasyon içinde yaygınlaşabilirler. Yüzyıllar içinde de, bu mutantlar sayıca artarak ormana egemen olur. Sonunda tüm popülasyon dört yıllık yeni döngüye uyum sağlar..
Bambuların Çiçeklenme Süreçleri Asal Çarpanlarla İlişkilidir
Modelin önemli bir sonucu daha vardır: Evrimsel süreç geriye doğru işlemez. Yani dört yıllık bir ormanda ortaya çıkan iki yıllık mutantlar, başarılı olamaz. Çünkü bu mutantlar, zamanın yarısında yalnız başına çiçek açacak ve yırtıcılara karşı hiçbir koruma sağlayamayacaktır. Bu durum, onların tohumlarının büyük kısmının yok olmasıyla sonuçlanır.
Veller ve ekibi, bu modelin milyonlarca yıl boyunca nasıl işlediğini test edebileceklerini fark etti. Teorik olarak, bambu türleri zaman içinde çiçeklenme döngülerini adım adım uzatmalıydı. Ancak bu değişim büyük sıçramalarla değil, küçük adımlarla gerçekleşmiş olmalıydı.
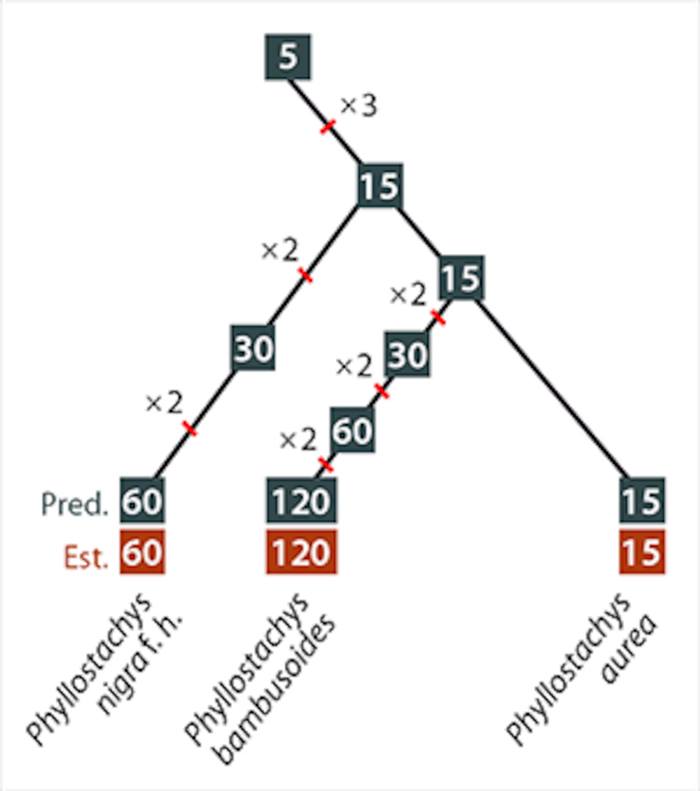
Bu nedenle, bambuların çiçeklenme süreleri genellikle küçük sayıların çarpımıyla elde edilen yıllar olmalıydı. Matematiksel veriler de bu modeli destekliyor:
- Bambusa bambos ise 32 yılda çiçek açar → 2 × 2 × 2 × 2 × 2
- Phyllostachys bambusoides 120 yılda bir çiçek açar → 5 × 3 × 2 × 2 × 2
- Phyllostachys nigra f. henonis 60 yılda bir çiçek açar → 5 × 3 × 2 × 2
Peki, türlerin çiçeklenme döngülerinin küçük asal sayıların çarpımıyla ifade edilmesi yalnızca bir tesadüf mü?
Veller ve ekibi bu soruya istatistiksel bir testle yanıt verdi. Çiçeklenme döngüsü iyi belgelenmiş bambu türlerini analiz ettiklerinde, bu döngülerin çoğunlukla küçük asal sayıların çarpımına dayandığını gördüler. Bu rastlantıyla açıklanamayacak kadar güçlü bir düzenlilikti. Hatta yapılan testin sonuçları istatistiksel olarak oldukça anlamlıydı (meraklısı için: p = 0.0041).
( Doğada matematiğe bir başka örnek için: Çiçek Simetrisi Nedir? Çiçeklerin Simetrik Olmasının Bir Avantajı Var mıdır?)
Sonuç Olarak
Bu modeli test etmek için hâlâ geniş bir alan bulunmaktadır. Pek çok bambu türünün uzun çiçeklenme döngüleri vardır; ancak bu döngüler şimdiye kadar yeterince hassas biçimde ölçülmemiştir. Örneğin, çiçeklenme süresi 23 yıl olan yeni bir Phyllostachys türü keşfedilirse, bu türün beş yıllık döngüye sahip bir atadan evrimleşmiş olması matematiksel olarak mümkün değildir.
Ancak bu modeli test etmek, sabır gerektiren bir iş. Çünkü bambuların çiçek açmasını gözlemlemek, bazı durumlarda onlarca yıl sürebiliyor. Bu da demek oluyor ki, bu teori ancak birkaç kuşak bilim insanının ortak çabasıyla kesin olarak doğrulanabilir.
Kaynaklar ve İleri Okumalar
- Bamboo Mathematicians. Yayınlanma tarihi: 15 mayıs 2015. Kaynak site: National Geographic. Bağlantı: Bamboo Mathematicians
- Veller C, Nowak MA, Davis CC. Extended flowering intervals of bamboos evolved by discrete multiplication. Ecol Lett. 2015 Jul;18(7):653-9. doi: 10.1111/ele.12442. Epub 2015 May 11. PMID: 25963600.
Matematiksel